《电磁场与电磁能》课程PPT教学课件（杨儒贵版）第二章 静电场

亥姆霍兹定理若矢量场F（）在无限区域中处处是单值的，且其导数连续有界，源分布在有限区域V中，则当矢量场的散度及旋度给定后，该矢量场F(r）可以表示为F(r) = -V@(r)+ V×A(r)F(r)V'.F(r)式中 Φ(r)=4元JVV'xF(rA(r) =L元JVrr可见，该定理表明任一矢量场均可表示为一个无旋场与一个无散场之和。矢量场的散度及旋度特性是研究失量场的首要问题

若矢量场 F (r) 在无限区域中处处是单值的， 且其 导数连续有界，源分布在有限区域 V  中，则当矢量场 的散度及旋度给定后，该矢量场 F (r) 可以表示为 亥姆霍兹定理 F(r)  (r)    A(r)         V dV ( ) 4π 1 ( ) r r F r  r V V         d ( ) 4π 1 ( ) r r F r A r 式中 可见，该定理表明任一矢量场均可表示为一个无旋 场与一个无散场之和。矢量场的散度及旋度特性是研究 矢量场的首要问题。 V ' z x y r O r' r – r' F(r)

第二章静电场主要内容电场强度、电位、介质极化、场方程、边界条件、能量与力2-1电场强度、电通及电场线电场对某点单位正电荷的作用力称为该点的电场强度，以E表示。Fqq库仑定律FE:(V/m)2e4元q式中q为试验电荷的电量，F为电荷q受到的作用力。电场强度通过任一曲面的通量称为电通，以表示，即E.ds=

第二章 静 电 场 主 要 内 容 电场强度、电位、介质极化、场方程、边界条件、能量与力 2-1 电场强度、电通及电场线 电场对某点单位正电荷的作用力称为该点的电场强度， 以 E 表示。 (V/m) q  F E 式中q 为试验电荷的电量，F 为电荷q 受到的作用力。 电场强度通过任一曲面的通量称为电通，以  表示， 即    S  E dS r r qq F e 2 4π   库仑定律

用电场线围电场线方程Exdl=0成电场管电场管轴线几种典型的电场线分布H带电平行板负电荷正电荷由此可见，电场线的疏密程度可以显示电场强度的大小

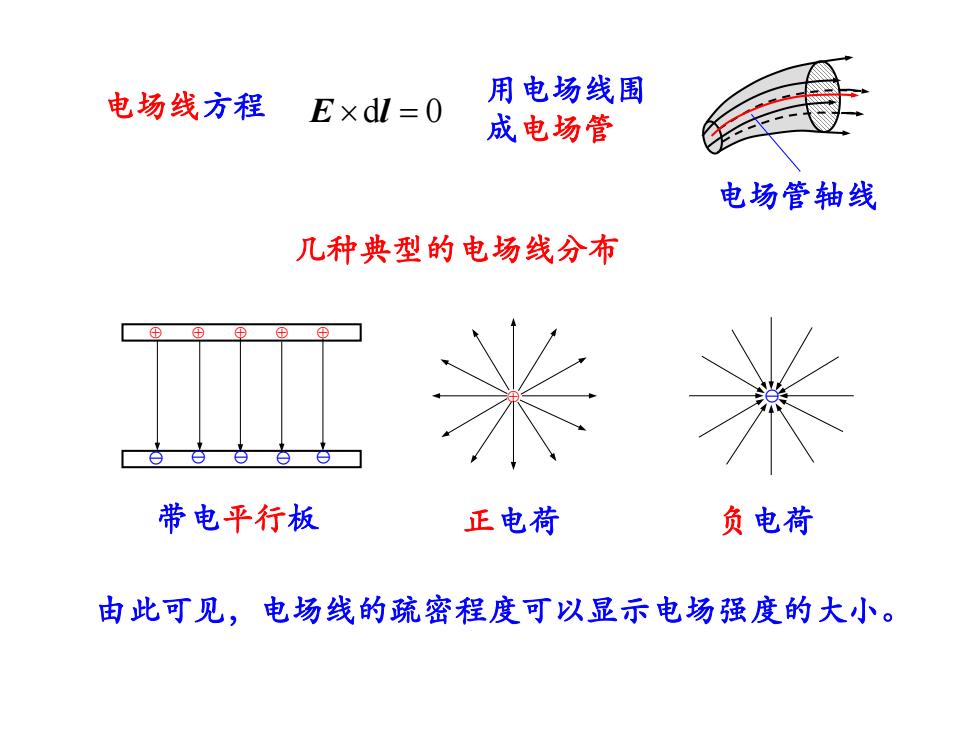
电场线方程 E  dl  0 用电场线围 成电场管           带电平行板  负电荷  正电荷 几种典型的电场线分布 由此可见，电场线的疏密程度可以显示电场强度的大小。 电场管轴线

2-2真空中静电场方程物理实验表明，真空中静电场的电场强度E满足下列两个积分形式的方程f.E.d=q E.dl=0%式中为真空介电常数。8o = 8.854187817...x10-12(F/m) x10-9(F/m)36元左式称为高斯定律，它表明真空中静电场的电场强度通过任一闭合曲面的电通等于该闭合曲面所包围的电量与真空介电常数之比。右式表明，真空中静电场的电场强度沿任一条闭合曲线的环量等于零

2-2 真空中静电场方程 物理实验表明，真空中静电场的电场强度E 满 足下列两个积分形式的方程 0 d S q     E S  d 0 l    E l  式中0 为真空介电常数。 左式称为高斯定律，它表明真空中静电场的电场强度 通过任一闭合曲面的电通等于该闭合曲面所包围的电 量与真空介电常数之比。右式表明，真空中静电场的 电场强度沿任一条闭合曲线的环量等于零。 10 (F/m) 36π 1 8.854187817 10 (F / m) 12 9 0       

根据上面两式可以求出电场强度的散度及旋度，即散度定理$.E.ds-1V.E=PS6080旋度定理Φ E.dl=0VxE=0上式表明，真空中静电场的电场强度在某点的散度等于该点的电荷体密度与真空介电常数之比。下式表明，真空中静电场的电场强度的旋度处处为零。由此可见，真空中静电场是有散无旋场

根据上面两式可以求出电场强度的散度及旋度，即 0     E    E  0 上式表明，真空中静电场的电场强度在某点的散 度等于该点的电荷体密度与真空介电常数之比。 下式表明，真空中静电场的电场强度的旋度处处 为零。 由此可见，真空中静电场是有散无旋场。 0 d S q     E S  d 0 l    E l  散度定理 旋度定理