
自动控制理论 结论: >幅值条件与K有关,相角条件与K无关 K=1.5 >满足相角条件的点必然满足幅值条件。 K=1 K-0.5 反之,满足幅值条件点未必能满足相角条件 幅值条件: 41 1 s+3 K 令s=o+jo代入上式,得 (o+3)2+o2=(4K)2 图4-5 >系统的等增益轨迹是一簇同心圆,对于某一个确定的K值,对应圆 周上有无穷多个S值都满足方程,其中只有同时满足相角条件的$值 才是方程的根。 >根轨迹就是S平面上满足相角条件点的集合。 6 第四章 根轨迹法 2025/1/14
( ) ( ) 2 2 2 3 4 1 3 4 K s j s K + + = = + = + 令 代入上式,得 6 第四章 根轨迹法 2025/1/14 ➢幅值条件与K有关,相角条件与K无关 ➢满足相角条件的点必然满足幅值条件。 反之,满足幅值条件点未必能满足相角条件。 自动控制理论 结论: 图4-5 幅值条件: ➢系统的等增益轨迹是一簇同心圆,对于某一个确定的K值,对应圆 周上有无穷多个S值都满足方程,其中只有同时满足相角条件的S值 才是方程的根。 ➢根轨迹就是S平面上满足相角条件点的集合

自动控制理论 >绘制根轨迹步骤 1)先找出S平面上满足相角条件的点,并把它们连成曲线: 2)用幅值条件确定相应点对应的K值。 例4-1求图4-1所示系统的根轨迹 解:1)用相角条件绘制根轨迹 G(s)= K s(+1) -ags+arg6s+1刃=±2k+1z,k=01,2, 2)用幅值条件确定增益K K=s s+1 例如s2=0.5,K=-0.50.5=0.25 第四章 根轨迹法 2025/1/14
−arg s + arg(s +1) = (2k +1),k = 0,1,2, 第四章 根轨迹法 2025/1/14 7 ➢绘制根轨迹步骤 1)先找出S平面上满足相角条件的点,并把它们连成曲线; 2)用幅值条件确定相应点对应的K值。 例4-1 求图4-1所示系统的根轨迹 解: 1)用相角条件绘制根轨迹 自动控制理论 ( ) (+1) = s K G s 2)用幅值条件确定增益K K = s s +1 例如s1,2 = −0.5,K = − 0.5 0.5 = 0.25
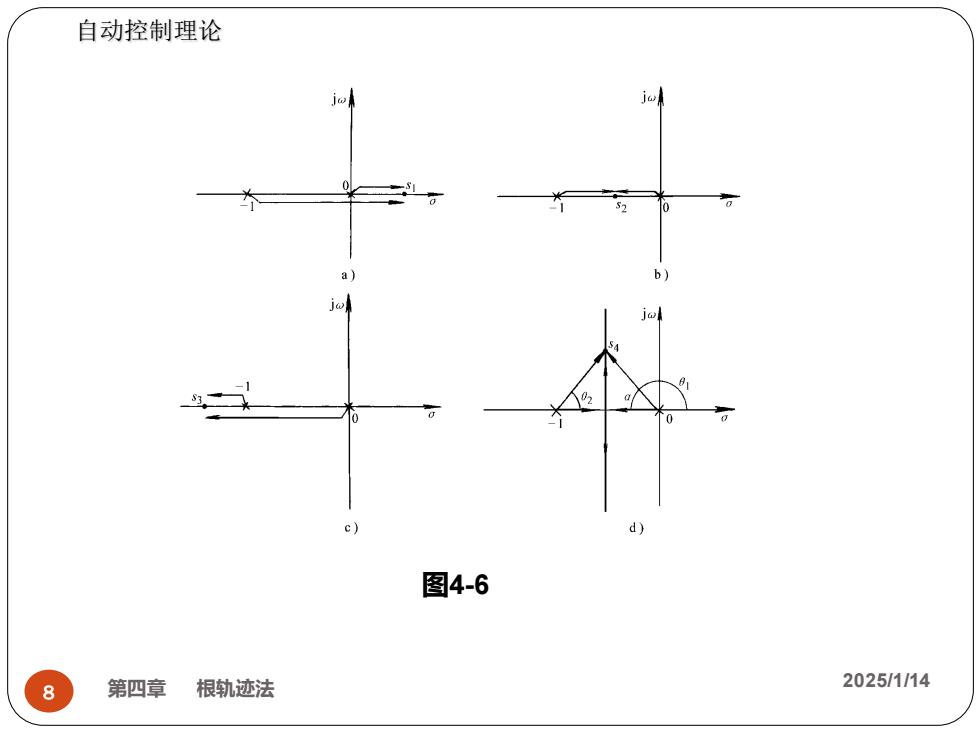
自动控制理论 d) 图4-6 8 第四章 根勃迹法 2025/1/14
第四章 根轨迹法 2025/1/14 8 图4-6 自动控制理论

自动控制理论 第二节根轨迹的基本规则 开环传递函数有如下两种表示: K(,s+1) G(s)H(s= n≥m (4-12) s+) 1=1 或 K6+z) G(s)H(s)= n≥m(4-13) T6+p,) 其中,K为系统的开环增益;K为系统的根轨迹增益它们之间的 关系为: 9 第四章 根轨迹法 2025/1/14
第二节 根轨迹的基本规则 9 第四章 根轨迹法 2025/1/14 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , (4 -13) , 4 -12 1 1 1 1 0 1 1 n m s p K s z G s H s n m T s K s G s H s n l l m i i n l l m i i + + = + + = = = = = 或 开环传递函数有如下两种表示: 自动控制理论 其中,K为系统的开环增益;K0为系统的根轨迹增益它们之间的 关系为:

自动控制理论 K ,n≥m (4-14) 1=1 来绘制根轨迹的基本规则 规则1:根轨迹的对称性 由于系统特征方程式的系数均为实数,因而特征根或为实数,或为 共轭复数.根轨迹必然对称于S平面的实轴 规则2:根轨迹的分支数及其起点和终点 闭环特征方程: (s+p)+KT(s+2,)=0 >当k由0→o变化时,方程中任一根由始点连续地向终点变化的轨迹称 为根轨迹的一条分支; 10 第四章 根轨迹法 2025/1/14
10 第四章 根轨迹法 2025/1/14 , (4 -14) 1 1 0 n m p K z K n l l m i i = = = 绘制根轨迹的基本规则 规则1:根轨迹的对称性 由于系统特征方程式的系数均为实数,因而特征根或为实数,或为 共轭复数.根轨迹必然对称于S平面的实轴 规则2:根轨迹的分支数及其起点和终点 闭环特征方程: ( ) ( ) 0 1 0 1 + + + = = = m i i n l l s p K s z 自动控制理论 ➢当k由 0 → 变化时,方程中任一根由始点连续地向终点变化的轨迹称 为根轨迹的一条分支;