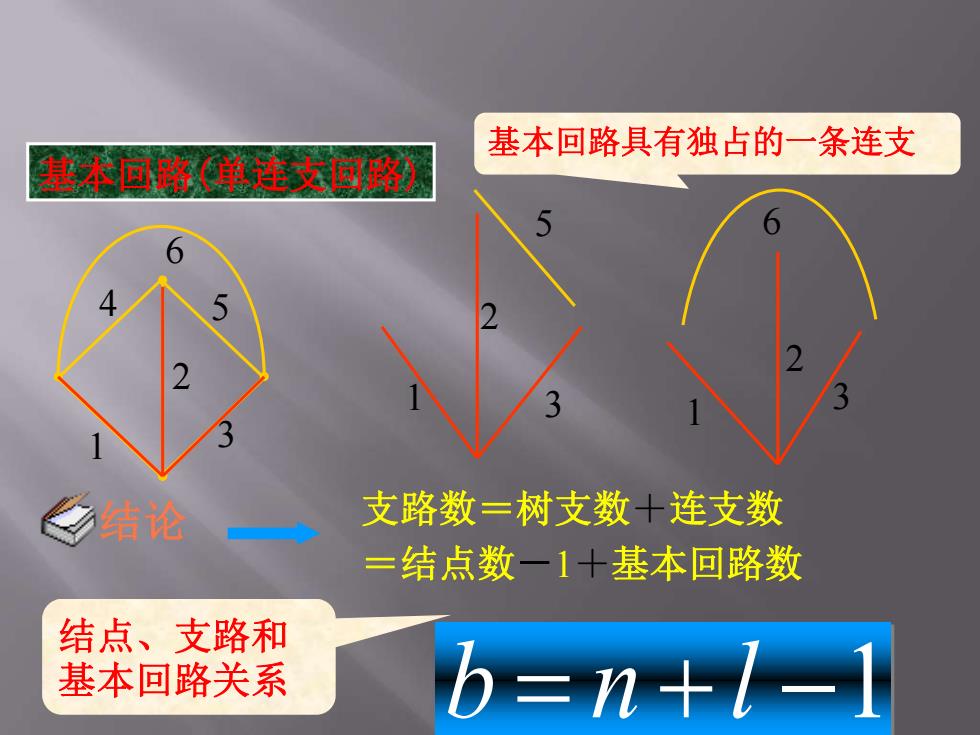
基本回路具有独占的一条连支 基本回路(单连支回路) 结论 支路数三树支数十连支数 =结点数一1十基本回路数 结点、支路和 基本回路关系 b=n+1-1
基本回路(单连支回路) 1 2 3 4 5 6 5 1 2 3 1 2 3 6 支路数=树支数+连支数 =结点数-1+基本回路数 b n l 1 结点、支路和 基本回路关系 基本回路具有独占的一条连支 结论
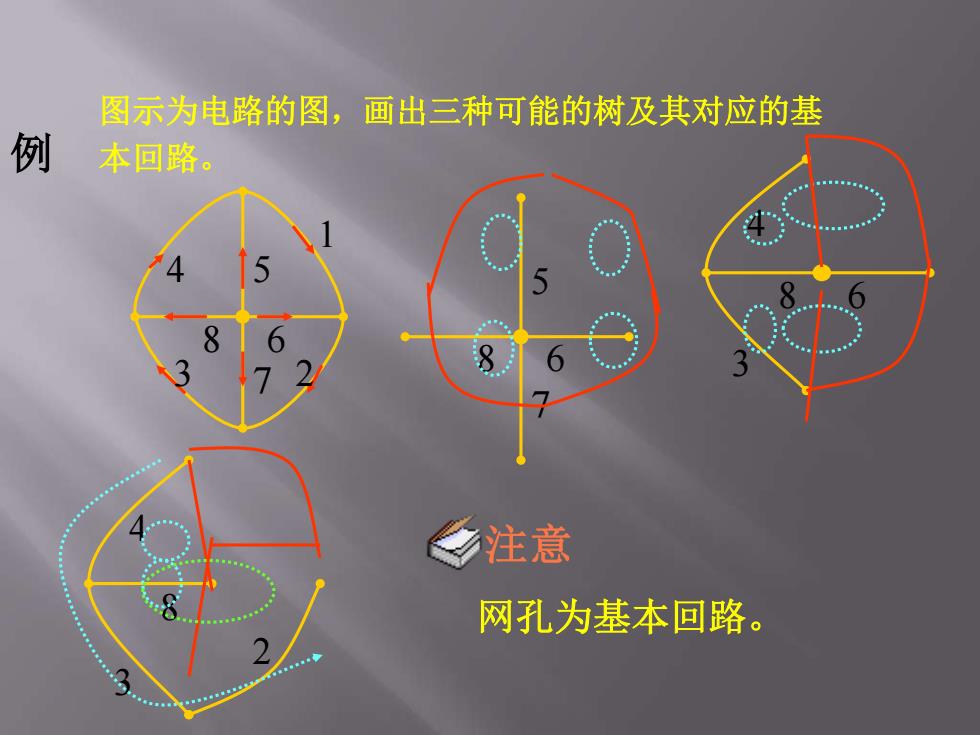
图示为电路的图,画出三种可能的树及其对应的基 例 本回路。 0 乡注意 网孔为基本回路
例 8 7 6 4 5 3 2 1 图示为电路的图,画出三种可能的树及其对应的基 本回路。 8 7 6 5 8 6 4 3 8 2 4 3 注意 网孔为基本回路
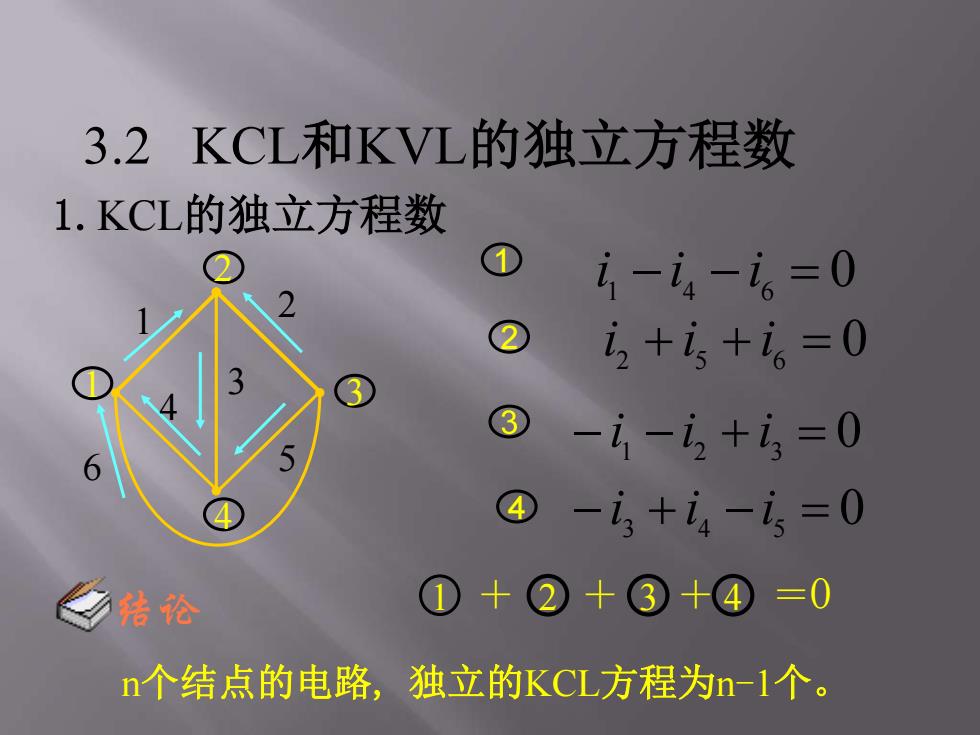
3.2KCL和KVL的独立方程数 1.KCL的独立方程数 1 i-i4-i6=0 i2+i,+6=0 3 -1-i2+i3=0 4 -i+i4-i=0 乡结论 ①+②+3+④=0 n个结点的电路,独立的KCL方程为n-1个
3.2 KCL和KVL的独立方程数 1.KCL的独立方程数 0 i 1 i 4 i 6 6 5 4 3 2 1 4 3 2 1 1 4 2 0 i 3 i 4 i 5 0 i 2 i 5 i 6 0 i 1 i 2 i 3 1 + 2 + 3 + 4 =0 n个结点的电路, 独立的KCL方程为n-1个。 结论

2.KVL的独立方程数 对网孔列KVL方程: u1+u3+u4=0 42+43-4=0 4+4-u6=0 u1-u2+u4+W,=0 乡注意 可以证明通过对以上三个网孔方程进 行加、减运算可以得到其他回路的KV工方程:
2.KVL的独立方程数 0 1 u1 u3 u4 3 2 0 u1 u2 u4 u5 0 u4 u5 u6 0 u2 u3 u5 1 - 2 6 5 4 3 2 1 4 3 2 1 对网孔列KVL方程: 可以证明通过对以上三个网孔方程进 行加、减运算可以得到其他回路的KVL方程: 注意

《结论 ①KVL的独立方程数=基本回路数b一(n一1) ②个结点、b条支路的电路,独立的KCL和KVL方 程数为: (n-1)+b-(n-1)=b
①KVL的独立方程数=基本回路数=b-(n-1) ②n个结点、b条支路的电路, 独立的KCL和KVL方 程数为: (n 1) b (n 1) b 结论