电子科技大学：《信号处理理论与算法》课程教学资源（课件讲稿）第三部分 CH04 Cohen类时频分布

Wigner分布与模糊函数 0.4 0.2 0 -02 -0.4 .100 50 0 50 100 0.5 0.4 0.3 0.2 X 0.1 0 20 40 60 80 100 120 (a)模糊函数，(b)时一频分布

4.2.2 x(t) 的模糊函数与时－频分布, (a) 模糊函数, (b) 时－频分布 Wigner分布与模糊函数

Vigner分布与模糊函数 将WVD的互项及（4.2.21)式均写成极坐标的形式，即： Ws (i,)=Ar(t,)expior(t,] (4.2.22a) Ax0)=A,(0,)explio(0, (4.2.22b) 由 （4.2.21)式，有 (0.7)=1 .6小0， (4.2.23a) 由（3.5.2) 式，有 (4.2.23b) 4.-gc-f小mar++] r)-2en-a--（- +4exp-a(-4)-i(Q-2.)cos[Q-Q.)+(-)Q.+Q4]

将WVD的互项及（4.2.21）式均写成极坐标的形式，即： （4.2.22a） （4.2.22b） 由（4.2.21）式，有 （4.2.23a） 由（3.5.2）式，有 （4.2.23b） W   t，  A t， j t， x x W W exp 1 2 ,   ， ，    ，  x x A A A A exp j 1 2 ,    A u  t      ，   A  u      ，   W d t   t   ，   W d t t      ，        1 2 2 2 , 1 1 exp exp 24 4 Axx d d u u du t j t t                          ，             2 2 2 1 2 2 1 2 exp 1 4exp cos i i i u u u d u d du Wt t t tt t tt t                                      ，  Wigner分布与模糊函数

Wigners分布与模糊函数 上式结果表明： WVD互项的相位对2和t的偏导数分别对应于该信号模 糊函数的互项的中心坐标，即(t,2)。AF中互项的位置直 接反映了WVD中交叉项的震荡状况。WVD中交叉项震荡越 厉害，那么，AF中互项的中心距(O,t)平面的原点越远。反 之，我们由AF互项的中心位置又可大致判断WVD互项的震 荡程度。 4r(6,2)=4 品4，uo)=n 4a-四0+f--]am[Ua+t+]

上式结果表明： WVD互项的相位对 和 的偏导数分别对应于该信号模 糊函数的互项的中心坐标，即 。AF中互项的位置直 接反映了WVD中交叉项的震荡状况。WVD中交叉项震荡越 厉害，那么，AF中互项的中心距 平面的原点越远。反 之，我们由AF互项的中心位置又可大致判断WVD互项的震 荡程度。  t   d d t ， ，        1 2 2 2 , 1 1 exp exp 24 4 Axx d d u u du t j tt                          ， W d   t t       W d   t t ，     ， Wigner分布与模糊函数

Wigners分布与模糊函数 WVD和AF各自互项与自项的位置及它们互项间的关 系提供了一个抑制WVD中交叉项的有效途径，即： (1)首先对xt)求模糊函数，由于A(O,)的自项始 终在平面(O,)的原点处，而互项远离原点，因此，我 们可设计一个(0，)平面的低通滤波器对A(0,t)滤波， 从而有效地抑制了A(0,)中的交叉项； (2)对滤波后的AF按（4.2.5)式作二维傅立叶变 换，得到W(t,2。这时Wt,2)的已是被抑制了交叉 项的新WVD

WVD和AF各自互项与自项的位置及它们互项间的关 系提供了一个抑制WVD中交叉项的有效途径，即： （1）首先对 求模糊函数，由于 的自项始 终在平面 的原点处，而互项远离原点，因此，我 们可设计一个 平面的低通滤波器对 滤波， 从而有效地抑制了 中的交叉项； （2）对滤波后的AF按（4.2.5）式作二维傅立叶变 换，得到 。这时 的已是被抑制了交叉 项的新WVD。 xt ，  Ax ，  Ax ，  Ax   ， ， Wx   t， W t， x Wigner分布与模糊函数

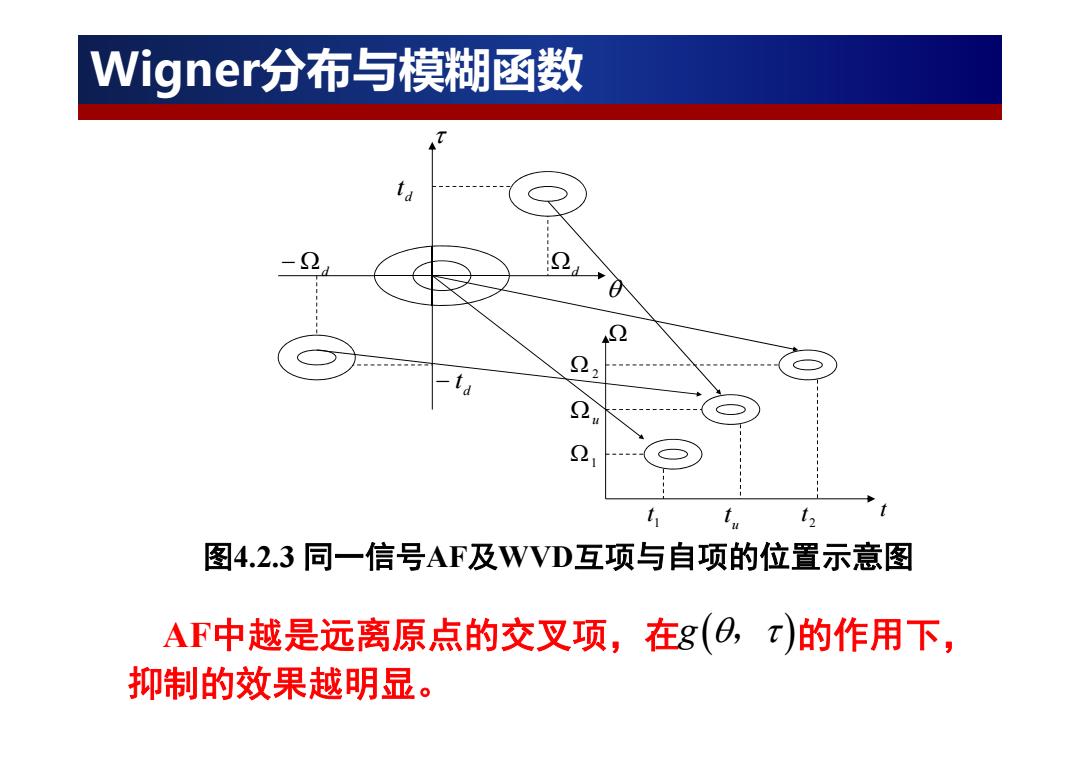
Wigner分布与模糊函数 t u 2 图4.2.3同一信号AF及WVD互项与自项的位置示意图 AF中越是远离原点的交叉项，在8(O,t)的作用下， 抑制的效果越明显

AF中越是远离原点的交叉项，在 的作用下， 抑制的效果越明显。   dt d  t  d d 1  2  u ut 1t 2 t  t 图4.2.3 同一信号AF及WVD互项与自项的位置示意图 g，  Wigner分布与模糊函数