电子科技大学：《信号处理理论与算法》课程教学资源（课件讲稿）第三部分 CH04 Cohen类时频分布

Wigner分布与模糊函数 WVD和AF的关系 FF E Ae 6,)=xt+d2xt-t2) W(t Fo FFo 图4.2.1 WVD和AF的关系

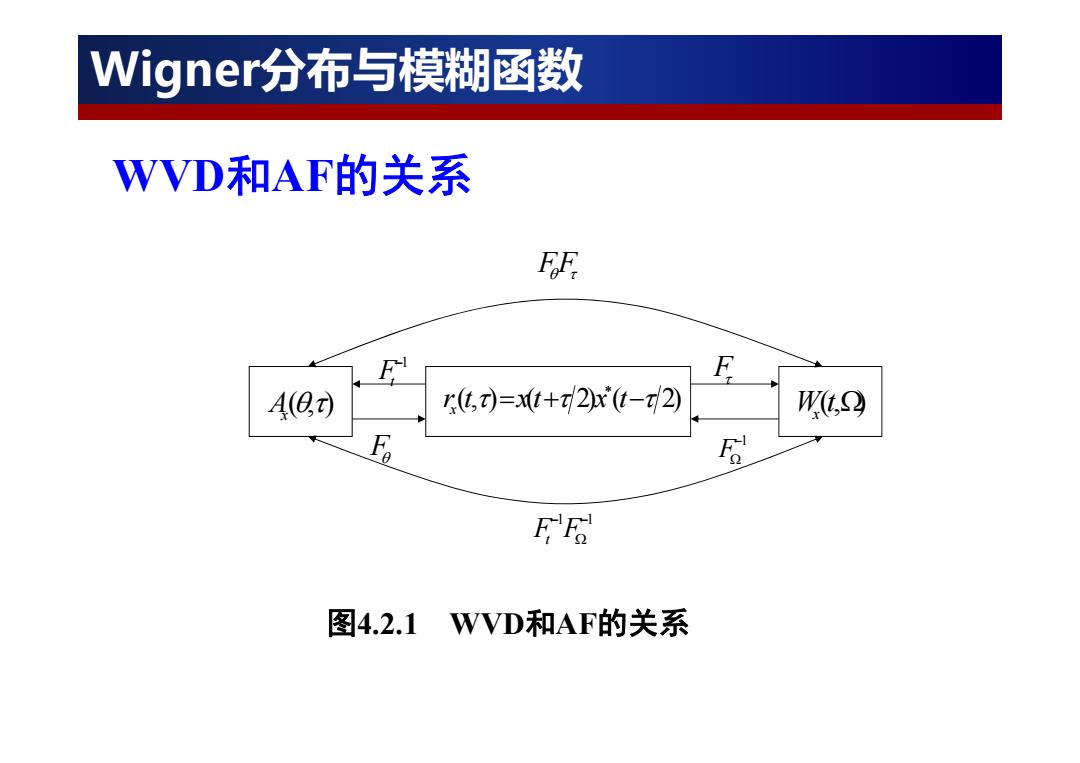
WVD和AF的关系 1 Ft F F 1 F FF (,) (  2) (  2)  r t x t x t x 1 1   Ft F (,) Ax W(t,) x 图4.2.1 WVD和AF的关系 Wigner分布与模糊函数

Vigner分布与模糊函数 课堂练习 求x()的模糊函数 0-[t-为] 已知)=erXo-径eu

课堂练习 求x(t)的模糊函数 已知     1 4 2 0 xt t t exp 2                2 /4 a a X e     ( )= Wigner分布与模糊函数   2t xt e 

Wigner分布与模糊函数 举例说明Wt,①和A(日，t)在(t,2)和(0，x)平面上的位 置的不同 例4.2.1 令 x()-aexp[-a(-1)/]espUQ (4.2.16) 我们在例3.3.5中已求出其WVD是 g6,0=2ep[-a-6}-(Q-1a(42.17) 同样可求出其模糊函数是 4ay2em{ae+小em[ua*o】 (4.2.18)

举例说明 和 在 和 平面上的位 置的不同 例4.2.1 令 （4.2.16 ） 我们在例3.3.5中已求出其WVD 是 （4.2.17 ） 同样可求出其模糊函数是 （4.2.18 ） (, ) W t x  (,) Ax   (, ) t  (,)         1 4 2 0 0 xt t t j t exp 2 exp                      2 2 0 0 2exp / Wt tt x            ，     2 2 0 0 1 1 exp exp 2 44 Ax j t                            ， Wigner分布与模糊函数

Wigners分布与模糊函数 分析结论： (1)W6,2)是实函数，而A(0,t)是复函数； (2)Wt,2的中心在(，2o)处，它是一高斯型函数， 时域、频域的扩展受O的控制； A,(g,)的中心在(0，)=(0,0处， 其幅值也是高斯型 函数，且受到一复正弦的调制。该复正弦在和轴方 向上的震荡频率由t和2所控制。这就是说，t,和2并 不影响A(,t)的中心位置，影响的只是其震荡速度。 w(69=2exp-au-6}'-(2-2,f1a 4a0+小m[Va+a]

分析结论： （1） 是实函数，而 是复函数； （2） 的中心在 处，它是一高斯型函数， 时域、频域的扩展受 的控制； 的中心在 处，其幅值也是高斯型 函数，且受到一复正弦的调制。该复正弦在 和 轴方 向上的震荡频率由 和 所控制。这就是说， 和 并 不影响 的中心位置，影响的只是其震荡速度。 Wx   t， ，  Ax ，  Ax   ， Ax Wx   t，   0，0 t  ， 0，0   0t 0t 0 0     2 2 0 0 1 1 exp exp 2 44 A j x t                            ，      2 2 0 0 2exp / Wt tt x             ， Wigner分布与模糊函数

Wigner分布与模糊函数 例4.2.2令 a)'oxpt-a (4.2.19) 其模糊函数（AF) 4(0,)=∑A,0,)+A(8,)+Ax8,）(42.20) A(O)及A(O,t是xd)的AF的互项，其中： 4a-em女o--[Ur+8】 式中1n=(6+2)/2,2=(但1+22)/2，t4=t-t,,24=2-22 因此 Aa)的中心为(8，)=(-2)=(2-2,4-52) A(8,)的中心为(0，t)=(2-ta)=(2-22:52-4)

例4.2.2 令 （4.2.19 ） 其模糊函数（AF）： (4.2.20) 及 是的AF的互项，其中： （4.2.21 ） 式中 ， ， ， 因此 的中心为 的中心为                    2 1 2 4 1 exp 2 i i i x t  t t j t       ， ， ， ， 1 2 2 1 , , 2 1 x x x x i Ax Ax A A i      ，  1 2 Ax ,x ，  2 1 Ax ,x x  t         1 2 2 2 , 1 1 exp exp 24 4 Axx d d u u du t j tt                           ，  1 2  2 ut tt    u   1   2  2 d 1 2  d  1   2 t  t  t   ，   ，， ，        d dt tt   2 11 2  1 2 Ax ,x   ， 2 1 Ax ,x       d d 1 221   ，        ，t tt ， Wigner分布与模糊函数