
4.方阵的幂及其性质 若A是n阶方阵,则A为A的k次幂,即 A=AA…A并且A"A=A+,(Am=A. k个 (m,k为自然数) 【注1】规定A°=E. 【思考】Ek=?答:Ek=E. 例9判断下列结论是否成立? (1)A2=0,则A=0 (2)(A+B)2=A+2AB+B2 (3)(E+A)2=E+2A+A2
4.方阵的幂及其性质 若A是 阶方阵,则 为A的 次幂,即 并且 n k A k k个 k A = A A A A A A , m k m+k = ( ) . mk m k A = A ( m, k 为自然数) 【注1】 规定 . 0 A E = 例9 判断下列结论是否成立? (1) 则 2 A O= , A O= (2) 22 2 () 2 A B A AB B + =+ + (3) 2 2 () 2 EA E AA + =+ + 【思考】 ? k E = : . k 答 E E =

【注2】由于矩阵乘法一般不满足交换律,即: AB≠BA,AB)≠AB. 【思考】什么条件下,有(AB)=AB? 答:AB=BA. 5.矩阵的转置 1 4 2 与B= 25 的关系.其中a=bi 2 8) 记B=A,A=BI
【注2】由于矩阵乘法一般不满足交换律,即: AB ≠ BA, (AB) A B . k k k ≠ 【思考】什么条件下,有 ( ) ? k k k AB A B = 答:AB=BA. 5. 矩阵的转置 分析 的关系. 1 4 122 2 5 458 2 8 A B = = 与 ij ji 其中 a b = 记 , . T T B AA B = =

定义设 2 … n 1 1 A= 21 2 A2n 与B= 2 12 A m2 (m2 Ain mxn nXm 称A,B互为转置矩阵,记B=AT,A=BI 即设A=(a)n’B=(bg)xm,若 aj=biyi=1,2,…m,j=1,2,…,n 称A,B互为转置矩阵. 8 例如 2 B=(8,2,4,6), BT= 4 (6
定义 设 11 12 1 11 21 1 21 22 2 12 22 2 1 2 1 2 n m n m m m mn n n mn a a a aa a a a a aa a A B aa a aa a = = 与 A B, , T T 称 互为转置矩阵,记 B AAB = = m n × n m× 即 设 Aa Bb = ( ij)m n× × , = ( ij)n m ,若 , 1,2, , 1,2, , ij ji a b i mj n = = = 称 A B, 互为转置矩阵. 例如 B = (8, 2, 4, 6 , ) 8 2 . 4 6 T B =

转置矩阵的运算性质 (①(4y=4;2)(4+B)y=AI+B;(3)(MY=MP; (4)(AB)=BA'; (5)r(A)=r(A). 推广(AA,…A-1An)/=AnA-1…A,A 例10Q=(-1,2,1),B=(1,1,-3),A=B,求Am
转置矩阵的运算性质 (1)(A ) A; T T = (2)( ) ; T T T A+ B = A + B (3)( ) ; T T λA = λA (4) ( ) T T T AB B A = ; 推广 12 1 1 2 1 ( )T T T TT AA A A A A A A n n nn − − = 例10 ( 1 2 1 ), (1 1 3 ), , . T n α =− = − = , , β , , A A α β 求 5 ( ) ( ). T ()rA rA =
6.方阵的行列式 定义由n阶方阵A的元素所构成的行列式, 叫做方阵A的行列式,记作A或detA. n阶矩阵 A的行列式 2 n 11 2 04 02 02n 4= L21 a2 An 02n ●●●● Ann 例A= 2 6 则A= 6 8 -2
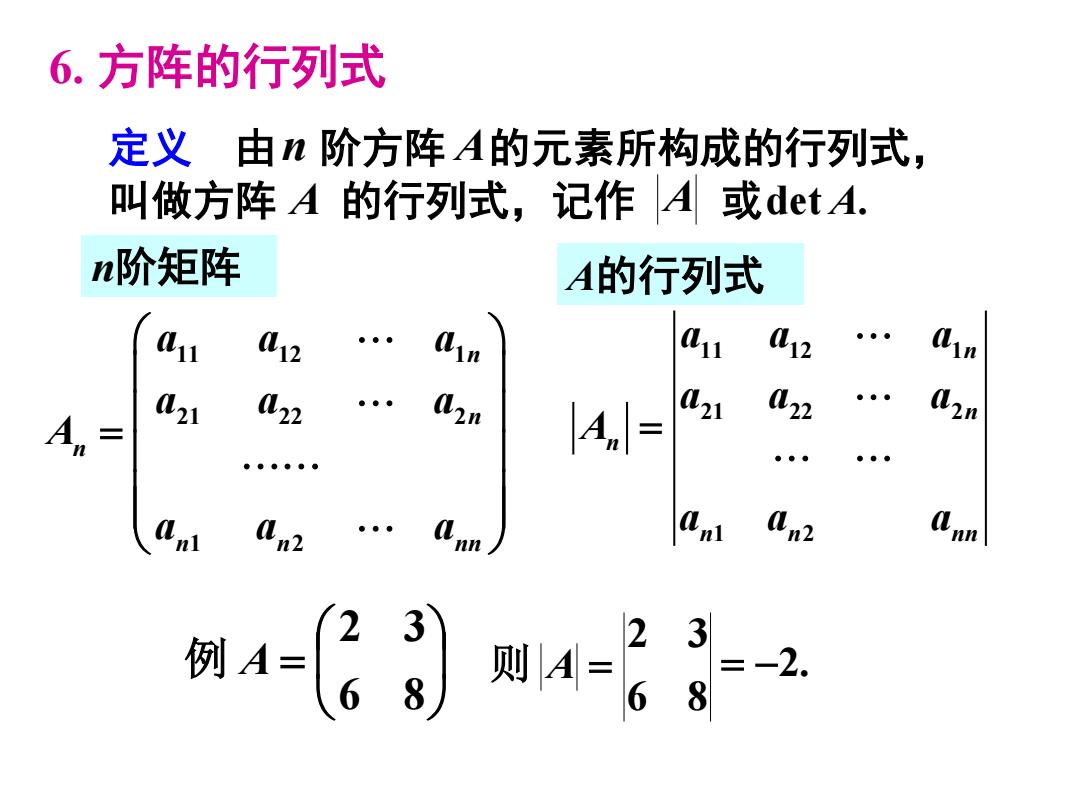
6. 方阵的行列式 定义 由 阶方阵 的元素所构成的行列式, 叫做方阵 的行列式,记作 或 n A A A det A. = 6 8 2 3 例 A 6 8 2 3 则 A = = −2. n阶矩阵 11 12 1 21 22 2 1 2 n n n n n nn aa a a a a A aa a = 11 12 1 21 22 2 1 2 n n n n n nn aa a aa a A aa a = A的行列式