
名闻手大学 二、 普通最小二乘法 SHIHEZI UNIVERSITY 1、最小二乘法产生的历史 ■2、最小二乘法的思路 >为了精确地描述Y与X之间的关系,必须使用这两个 变量的每一对观察值,才不至于以点概面 > Y与X之间是否是直线关系?在Y与X的散点图上画出 直线的方法很多。任务?—找出一条能够最好地 描述Y与X(代表所有点)之间的直线。 >什么是最好?找出判断“最好”的原则:最好指 得是找一条直线使得这些点到该直线的纵向距离的 和(平方和)最小 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 17 ◼ 1、最小二乘法产生的历史 ◼ 2、最小二乘法的思路 ➢ 为了精确地描述Y与X之间的关系,必须使用这两个 变量的每一对观察值,才不至于以点概面 ➢ Y与X之间是否是直线关系?在Y与X的散点图上画出 直线的方法很多。任务?——找出一条能够最好地 描述Y与X(代表所有点)之间的直线。 ➢ 什么是最好?—找出判断“最好”的原则:最好指 得是找一条直线使得这些点到该直线的纵向距离的 和(平方和)最小 二、普通最小二乘法
石所多大学 二、普通最小二乘法 SHIHEZI UNIVERSITY 兰种距离 纵向距离a,=Y,-乎.=Y,-B。BX AX,Y)横向距离 纵向距离 距离 A为实际点,B为拟合 直线上与之对应的点 2024/9/22 石河子大学经管学院一一唐勇 18
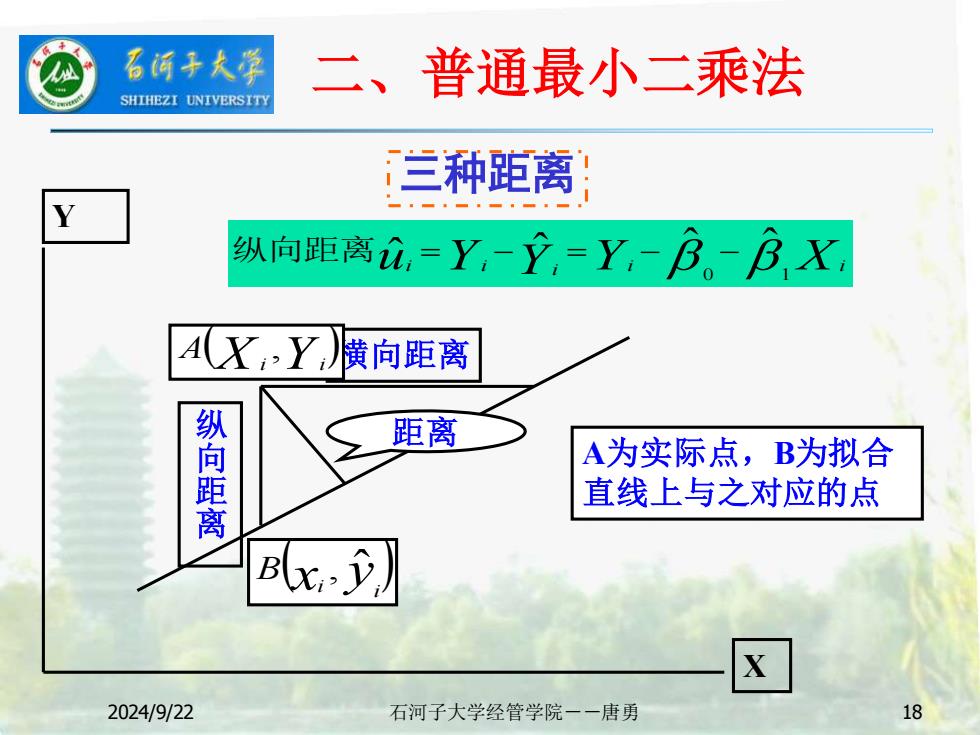
2024/9/22 石河子大学经管学院--唐勇 18 Y X 纵 向 距 离 横向距离 距离 (X Y ) i i A , (x y ) i i B , ˆ A为实际点,B为拟合 直线上与之对应的点 u Y Y Yi Xi i i i ˆ ˆ ˆ ˆ 0 1 纵向距离 = − = − − 二、普通最小二乘法 三种距离

名两子大学 二、 普通最小二乘法 SHIHEZI UNIVERSITY 人们设想的拟合准则有: min -) 误差相互抵消,达不到要求 =1 2 min - 不能保证估计的无 偏性,计算也难。 3 min 仅考虑个别点的影响 不存在误差相互抵消问题, min 20g- 考虑了所有点的影响,估计 具有较好的估计性质 一最小二乘准则 Ordinary Least Squares
2024/9/22 石河子大学经管学院--唐勇 19 二、普通最小二乘法

石闭手大学 二、普通最小二乘法 SHIHEZI UNIVERSITY 3、最小二乘法的数学原理 0=∑g-)P=2,-(a。+Bx,》月 ∑(B。+BX,-I)=0 ∑(。+B,x,-I)x,=0 或 I,=n。+B,X1 EYX:BOEX:+BEX EX'EY -EX EYX 解得: nX,-(X,)2 A= n∑YX,-I,X nEX2-X )2 2024/9/22 石河于大子经官子阮一一唐男 20
2024/9/22 石河子大学经管学院--唐勇 20 = − = − + n i i i n Q Yi Y Y X 1 2 0 1 2 1 )) ˆ ˆ ) ( ( ˆ ( 3、最小二乘法的数学原理 二、普通最小二乘法

名两子大学 二、普通最小二乘法 SHIHEZI UNIVERSITY 记 ∑号=∑x,-=∑x-(x》 ∑xy=∑(X-Xg-T)=∑Xy-∑x,∑y 上述参数估计量可以写成:A=x丛 Ex2 B。=7-B,X 称为OLS估计量的离差形式(deviation form) 由于参数的估计结果是通过最小二乘法得到的, 故称为普通最小二乘估计量(ordinary least squares estimators)。 2024/9/22 石河子大学经管学院一一唐勇 21
2024/9/22 石河子大学经管学院--唐勇 21 记 ( ) 2 2 2 2 1 i = ( i − ) = i − Xi n x X X X i i = i − i − = i i − XiYi n x y X X Y Y X Y 1 ( )( ) 上述参数估计量可以写成: = − = Y X x x y i i i 0 1 1 2 ˆ ˆ ˆ 称为OLS估计量的离差形式(deviation form)。 由于参数的估计结果是通过最小二乘法得到的, 故称为普通最小二乘估计量(ordinary least squares estimators)。 二、普通最小二乘法