
第3章动量定理及其守恒定律习题解答 15 第3章动量定理及其守恒定律习题解答 第三章基本知识小结 在转动参考系中:。=mo27,'=2mm×而 1牛顿运动定律适用于惯性系、质点,牛顿第二定律是核心。 5.质心和质心运动定理 矢量式:F=ma=m,=m m.=∑m,m.=∑m,ma。=∑m,a dt ②∑F=ma. F.=1a,F,=ma,F=ma:(直角坐标) (注意分量式的运用) 分量式: F.ma.m- n,Fn=ma,=m二(孤坐标) 2动量定理适用于惯性系、质点、质点系。 导数形式:F=匝 d 微分形式:Fd= 积分形式:i(=「Fd)=△p (注意分量式的运用) 3动量守恒定律适用于惯性系、质点、质点系。 若作用于质点或质点系的外力的矢量和始终为零,则质点或质 点系的动量保持不变。即 若∑F外=0,则刀=恒矢量。 (注意分量式的运用) 4在非惯性系中,考虑相应的惯性力,也可应用以上规律解题。 在直线加速参考系中:子=-md
第 3 章动量定理及其守恒定律习题解答 15 第 3 章动量定理及其守恒定律习题解答 第三章基本知识小结 ⒈牛顿运动定律适用于惯性系、质点,牛顿第二定律是核心。 矢量式: 2 2 dt d r m dt dv F ma m = = = 分量式: (弧坐标) (直角坐标) 2 , , , v F ma m dt dv F ma m F ma F ma F ma n n x x y y z z = = = = = = = ⒉动量定理适用于惯性系、质点、质点系。 导数形式: dt dp F = 微分形式: Fdt dp = 积分形式: I Fdt p = = ( ) (注意分量式的运用) ⒊动量守恒定律适用于惯性系、质点、质点系。 若作用于质点或质点系的外力的矢量和始终为零,则质点或质 点系的动量保持不变。即 若F外 = ,则 p = 恒矢量。 0 (注意分量式的运用) ⒋在非惯性系中,考虑相应的惯性力,也可应用以上规律解题。 在直线加速参考系中: 0 * f ma = − 在转动参考系中: = , = 2 ' * 2 * f m r f mv c k ⒌质心和质心运动定理 ⑴ c = i i c = i i mac =miai mr m r mv m v ⑵ F = mac (注意分量式的运用)

第3章动量定理及其守恒定律习题解答 16 第3章动量定理及其守恒定律习题解答 3.5.1质量为2kg的质点的运动学方程为 度至少等于3.92米/秒2,才能使谷物与筛面发生相对运动。 F=(612-1)i+(312+31+1)j(单位:米,秒),求证质点受恒力 m 而运动,并求力的方向大小。 m2 解:a=d27/d2=12i+6j,F=ma=24i+12j为一 与时间无关的恒矢量,,质点受恒力而运动。 3.5.3题图 3.5.4题图 F=242+122)2=12V5N,力与x轴之间夹角为: 3.5.4桌面上叠放若两块木板,质量各为m,m2,如图所示,mz a arcigF,/F,arctg0.5 =26034 和桌面间的摩擦系数为μ2,m1和m间的摩擦系数为μ1.问沿水平 方向用多大的力才能把下面的木板抽出来。 解:以地为参考系,隔离m1、m,其受力与运动情况如图所示, 3.5.2质量为m的质点在0-xy平面内运动,质点的运动学方程 6 f' N2 N 为:F=acosoti+bsinotj,ab,w为正常数,证明作用于质点 a 的合力总指向原点。 Nr' mig 证明::a=d7/dh2=-o2(acosoti+bsin og)=-o2行 其中,N=N1,f-f=uN,=u2N2,选图示坐标系o-y,对m1,m2 分别应用牛顿二定律,有 F=md=-mo2行,∴.作用于质点的合力总指向原点。 4,N1=m1a N1-m1g=0 解方程 3.5.3在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷 F-4,N1-42N2=m2a2N2-N1-m2g=0 粒,一方面逐出秸杆,筛面微微倾斜,是为了从较低的一边将秸杆 逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才 组,得a1=41ga2=(F-4mg-42m,g-422g)/m2 可能将谷粒筛出,若谷粒与筛面静摩擦系数为0.4,问筛沿水平方向 要把木板从下面抽出来,必须满足a2>a1,即 的加速度至少多大才能使谷物和筛面发生相对运动? 解:以地为参考系,设谷物的质量为,所受到的最大静摩擦 F-4m18-42m8-μ2m28>mL8 力为∫=4。mg,谷物能获得的最大加速度为 ∴.F>(,t42m+m2g a=f1m=4。g=0.4×9.8=3.92m/s2∴.筛面水平方向的加速
第 3 章动量定理及其守恒定律习题解答 16 第 3 章动量定理及其守恒定律习题解答 3.5.1 质量为 2kg 的质点的运动学方程为 r t i t t j ˆ (3 3 1) ˆ (6 1) 2 2 = − + + + (单位:米,秒), 求证质点受恒力 而运动,并求力的方向大小。 解:∵ a d r dt i j 12 ˆ 6 ˆ / 2 2 = = + , F ma i j = = 24 ˆ +12 ˆ 为一 与时间无关的恒矢量,∴质点受恒力而运动。 F=(242+122 ) 1/2=12 5 N,力与 x 轴之间夹角为: = arctgF / F = arctg0.5 = 2634' y x 3.5.2 质量为 m 的质点在 o-xy 平面内运动,质点的运动学方程 为: r a t i b t j ˆ = cos ˆ + sin ,a,b,ω为正常数,证明作用于质点 的合力总指向原点。 证明:∵ a d r dt a ti b tj r 2 2 2 2 ) ˆ = / = − ( cos ˆ + sin = − F ma m r 2 = = − , ∴作用于质点的合力总指向原点。 3.5.3 在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷 粒,一方面逐出秸杆,筛面微微倾斜,是为了从较低的一边将秸杆 逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才 可能将谷粒筛出,若谷粒与筛面静摩擦系数为 0.4,问筛沿水平方向 的加速度至少多大才能使谷物和筛面发生相对运动? 解:以地为参考系,设谷物的质量为 m,所受到的最大静摩擦 力为 f = omg ,谷物能获得的最大加速度为 2 a f / m g 0.4 9.8 3.92 m /s = = o = = ∴筛面水平方向的加速 度至少等于 3.92 米/秒 2,才能使谷物与筛面发生相对运动。 μ1 μ2 3.5.3 题图 3.5.4 题图 3.5.4 桌面上叠放着两块木板,质量各为 m1 ,m2,如图所示,m2 和桌面间的摩擦系数为μ2,m1 和 m2 间的摩擦系数为μ1,问沿水平 方向用多大的力才能把下面的木板抽出来。 解:以地为参考系,隔离 m1、m2,其受力与运动情况如图所示, 其中,N1'=N1,f1'=f1=μ1N1,f2=μ2N2,选图示坐标系 o-xy,对 m1,m2 分别应用牛顿二定律,有 0 0 1 1 2 2 2 2 2 1 2 1 1 1 1 1 1 − − = − − = = − = F N N m a N N m g N m a N m g 解方程 组,得 ( ) 1 1 2 1 1 2 1 2 2 2 a = g a = F − m g − m g − m g / m 要把木板从下面抽出来,必须满足 a2 a1 ,即 F − 1m1g − 2m1g − 2m2 g m2 1g F ( 1+ 2 )(m1 + m2 )g m2 m1 F m1g f1 N1 a2 a1 N2 N1' m2g f2 f1' F x y
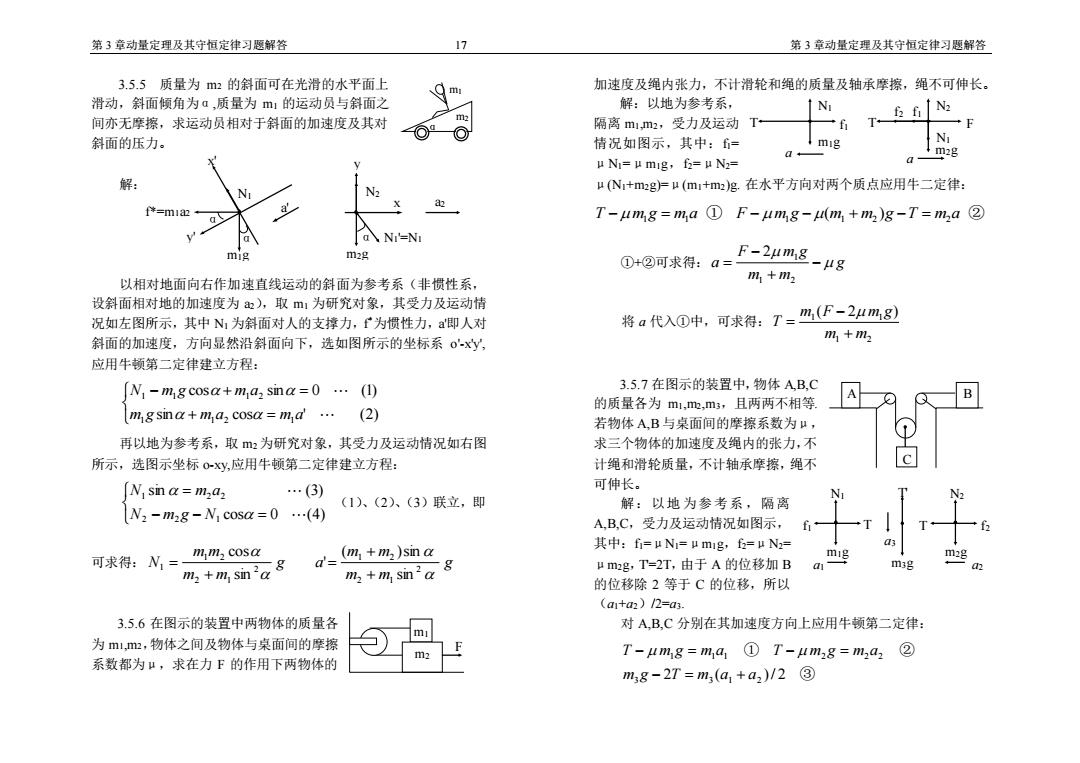
第3章动量定理及其守恒定律习题解答 17 第3章动量定理及其守恒定律习题解答 3.5.5质量为m2的斜面可在光滑的水平面上 加速度及绳内张力,不计滑轮和绳的质量及轴承摩擦,绳不可伸长。 滑动,斜面倾角为a,质量为m1的运动员与斜面之 解:以地为参考系, Ni 间亦无摩擦,求运动员相对于斜面的加速度及其对 m2 隔离m1,m2,受力及运动T 一f 入 斜面的压力。 情况如图示,其中:= mig m2g μN1=um1g,f=uN2= 解: μ(N+m2g尸μ(m1+m2)培.在水平方向对两个质点应用牛二定律: N *=mia T-4mg=m,a①F-4mg-4m,+m2)g-T=m,a② [a\NI'=NI mig m2g F-24m18 ①+②可求得:a= -μ8 以相对地面向右作加速直线运动的斜面为参考系(非惯性系, m1+m2 设斜面相对地的加速度为),取m1为研究对象,其受力及运动情 况如左图所示,其中N为斜面对人的支撑力,为惯性力,即人对 将a代入①中,可求得:T=m(F-2mg 斜面的加速度,方向显然沿斜面向下,选如图所示的坐标系o'xy, m1+m2 应用牛顿第二定律建立方程: (N -mg cosa+maz sina=0...(1) 3.5.7在图示的装置中,物体AB,C B 的质量各为m1,m2,m3,且两两不相等 mg smna+m a cosa m a... (2) 若物体A,B与桌面间的摩擦系数为μ, 再以地为参考系,取2为研究对象,其受力及运动情况如右图 求三个物体的加速度及绳内的张力,不 所示,选图示坐标0-xy,应用牛顿第二定律建立方程: 计绳和滑轮质量,不计轴承摩擦,绳不 N sin a m2az …(3) 可伸长。 (1)、(2)、(3)联立,即 解:以地为参考系,隔离 N2-m2g-N cosa=0.(4) AB,C,受力及运动情况如图示, f 可求得:N,= mm cosa =(m +m )sin a 其中:fi=uN=μm1g,f=μN2= mig m2g 8 m3g m2 +m sin2a m2 +m sin2a um2g,T=2T,由于A的位移加B 的位移除2等于C的位移,所以 (a1+a2)/2=a3. 3.5.6在图示的装置中两物体的质量各 对A,B,C分别在其加速度方向上应用牛顿第二定律: 为m1,2,物体之间及物体与桌面间的摩擦 T-4mg=m,a1①T-4m2g=ma2② 系数都为u,求在力F的作用下两物体的 m8-2T=m3(a1+a2)/2③
第 3 章动量定理及其守恒定律习题解答 17 第 3 章动量定理及其守恒定律习题解答 3.5.5 质量为 m2 的斜面可在光滑的水平面上 滑动,斜面倾角为α,质量为 m1 的运动员与斜面之 间亦无摩擦,求运动员相对于斜面的加速度及其对 斜面的压力。 解: 以相对地面向右作加速直线运动的斜面为参考系(非惯性系, 设斜面相对地的加速度为 a2),取 m1 为研究对象,其受力及运动情 况如左图所示,其中 N1 为斜面对人的支撑力,f *为惯性力,a'即人对 斜面的加速度,方向显然沿斜面向下,选如图所示的坐标系 o'-x'y', 应用牛顿第二定律建立方程: + = − + = sin cos ' (2) cos sin 0 (1) 1 1 2 1 1 1 1 2 m g m a m a N m g m a 再以地为参考系,取 m2 为研究对象,其受力及运动情况如右图 所示,选图示坐标 o-xy,应用牛顿第二定律建立方程: − − = = cos 0 (4) sin (3) 2 2 1 1 2 2 N m g N N m a (1)、(2)、(3)联立,即 可求得: g m m m m g a m m m m N 2 2 1 1 2 2 2 1 1 2 1 sin ( )sin ' sin cos + + = + = 3.5.6 在图示的装置中两物体的质量各 为 m1,m2,物体之间及物体与桌面间的摩擦 系数都为μ,求在力 F 的作用下两物体的 加速度及绳内张力,不计滑轮和绳的质量及轴承摩擦,绳不可伸长。 解:以地为参考系, 隔离 m1,m2,受力及运动 情况如图示,其中:f1= μN1=μm1g,f2=μN2= μ(N1+m2g)=μ(m1+m2)g. 在水平方向对两个质点应用牛二定律: T − m1g = m1a ① F − m1g − (m1 + m2 )g −T = m2a ② ①+②可求得: g m m F m g a − + − = 1 2 2 1 将 a 代入①中,可求得: 1 2 1 1 ( 2 ) m m m F m g T + − = 3.5.7 在图示的装置中,物体 A,B,C 的质量各为 m1,m2,m3,且两两不相等. 若物体 A,B 与桌面间的摩擦系数为μ, 求三个物体的加速度及绳内的张力,不 计绳和滑轮质量,不计轴承摩擦,绳不 可伸长。 解:以地 为参考系 ,隔离 A,B,C,受力及运动情况如图示, 其中:f1=μN1=μm1g,f2=μN2= μm2g,T'=2T,由于 A 的位移加 B 的位移除 2 等于 C 的位移,所以 (a1+a2)/2=a3. 对 A,B,C 分别在其加速度方向上应用牛顿第二定律: ③ ① ② 3 2 3 ( 1 2 )/ 2 1 1 1 2 2 2 m g T m a a T m g m a T m g m a − = + − = − = m1 m2 α m1 m2 F f1 N1 m1g T a F N2 m2g T a N1 f2 f1 C A B f1 T N1 m1g a1 T f2 N2 m2g a2 T' m3g a3 y N2 x a2 α N1'=N1 m2g α x' N1 a' f*=m1a2 y' m1g α

第3章动量定理及其守恒定律习题解答 18 第3章动量定理及其守恒定律习题解答 ①,②,③联立,可求得: [斜截式方程y=kx+b,两点式方程(y-y1)M(x-x=(y2-y)Mx2x] 2m2m3(1+μ) 00 0.05 008 a1= 由动量定理:m△v=Ft= L(m1+m2)m3+4m1m2 ∫6器1dh+器(0.08-t)d 005 2m,m3(1+4) 可求得Fmx=245N a2= L(m1+m2)m3+4m,m2 3.5.12沿铅直向上发射玩具火箭的推力随时间变化如图所示, (m1+m2)m3(1+μ) 03= -u 火箭质量为2kg,=0时处于静止,求火箭发射后的最大速率和最大 (m1+m2)m3+4m1m2 高度(注意,推力大于重力时才启动)。 F(N) 3.5.8天平左端挂一定滑轮,一轻绳跨过定滑轮,绳的两端分别 解:根据推力Ft图像,可知F=4.9t 98 系上质量为m1m2的物体(m1≠m),天平右端的托盘上放有砝码.问 (t≤20),令F=mg,即4.9t=2×9.8,=4s t(s) 天平托盘和砝码共重若干,天平才能保持平衡?不计滑轮和绳的质 因此,火箭发射可分为三个阶段:=0一4s 量及轴承摩擦,绳不伸长。 为第一阶段,由于推力小于重力,火箭静 20 解:隔离m1,m及定滑轮,受力及运动情 止,v=0,y=0:t=4一20s为第二阶段,火箭作变加速直线运动,设=20s 况如图示,应用牛顿第二定律: 时,y=y1,v=vmx:t≥20s为第三阶段,火箭只受重力作用,作 T-mg=m,a①m2g-T=m2a②T=2T 竖直上抛运动,设达最大高度时的坐标yy2 mm: 第二阶段的动力学方程为:F-mg=m dv/dt Y 由①②可求得: dy F mdt-gdt =4.9/2tdt-9.8dt T=2mmg T=2mmag 5dm=4.9/2td-9.8dht≤20) m1+m2 m1+m2 v=4.9/4t2-9.81+4×4.9(t≤20 mig m2g T 所以,天平右端的总重量应该等于T,天 'ms=(20)=314m/s 平才能保持平衡。 d=vd=(4.9/4t2-9.8t+4×4.9)dh 3.5.11棒球质量为0.14kg,用棒击棒球的力随时间的变化如图所 ∴6d=4.9/4012dh-9.81d+4x4.92dh 示,设棒球被击前后速度增量大小为70ms,求力的最大值,打击时, 不计重力。 片=1672m 解:由F一t图可知: FN) 第三阶段运动学方程 当0≤t≤0.05时,F=点F v=314-9.8(t-20)(1),y-y=314(t-20)-4.91-20)2(2) 当0.05≤1≤0.08时,F=86皓Fm 0.050.08ts) 令v=0,由(1)求得达最大高度y2时所用时间(t-20)=32,代入(2)
第 3 章动量定理及其守恒定律习题解答 18 第 3 章动量定理及其守恒定律习题解答 Y Y2 Y1 0 ①,②,③联立,可求得: g m m m m m m m m a g m m m m m m m a g m m m m m m m a − + + + + = − + + + = − + + + = 1 2 3 1 2 1 2 3 3 1 2 3 1 2 1 3 2 1 2 3 1 2 2 3 1 ( ) 4 ( ) (1 ) ( ) 4 2 (1 ) ( ) 4 2 (1 ) 3.5.8 天平左端挂一定滑轮,一轻绳跨过定滑轮,绳的两端分别 系上质量为 m1,m2 的物体(m1≠m2),天平右端的托盘上放有砝码. 问 天平托盘和砝码共重若干,天平才能保持平衡?不计滑轮和绳的质 量及轴承摩擦,绳不伸长。 解:隔离 m1,m2 及定滑轮,受力及运动情 况如图示,应用牛顿第二定律: ' ' 2 ' T −m1g = m1a ① m2 g −T = m2a ②T = T 由①②可求得: 1 2 1 2 1 2 1 2 2 , 2 ' m m m m g T m m m m g T + = + = 所以,天平右端的总重量应该等于 T,天 平才能保持平衡。 3.5.11 棒球质量为 0.14kg,用棒击棒球的力随时间的变化如图所 示,设棒球被击前后速度增量大小为 70m/s,求力的最大值,打击时, 不计重力。 解:由 F—t 图可知: 0.03 max 0.08 0.05 max 0.05 0.08 0 0.05 t F F t F F t t − = = 当 时, 当 时, [斜截式方程 y=kx+b,两点式方程 (y-y1)/(x-x1)=(y2-y1)/(x2-x1)] 由动量定理: = = + − 0.08 0.05 0.03 0.05 0 0.05 0.08 0 (0.08 ) max max m v Fdt tdt t dt F F 可求得 Fmax = 245N 3.5.12 沿铅直向上发射玩具火箭的推力随时间变化如图所示, 火箭质量为 2kg,t=0 时处于静止,求火箭发射后的最大速率和最大 高度(注意,推力大于重力时才启动)。 解:根据推力 F-t 图像,可知 F=4.9t (t≤20),令 F=mg,即 4.9t=2×9.8,t=4s 因此,火箭发射可分为三个阶段:t=0—4s 为第一阶段,由于推力小于重力,火箭静 止,v=0,y=0;t=4—20s 为第二阶段,火箭作变加速直线运动,设 t=20s 时,y = y1,v = vmax ;t≥20s 为第三阶段,火箭只受重力作用,作 竖直上抛运动,设达最大高度时的坐标 y=y2. 第二阶段的动力学方程为:F- mg = m dv/dt ( ) ( ) y m dy t dt tdt dt dy vdt t t dt v v m s v t t t dv tdt dt t dv F mdt gdt tdt dt y v t t 1672 4.9 / 4 9.8 4 4.9 (4.9 / 4 9.8 4 4.9) (20) 314 / 4.9 / 4 9.8 4 4.9 20 4.9 / 2 9.8 20 / 4.9 / 2 9.8 1 20 4 20 4 20 4 2 0 2 max 2 0 4 4 1 = = − + = = − + = = = − + = − = − = − 第三阶段运动学方程 314 9.8( 20) (1), 314( 20) 4.9( 20) (2) 2 v = − t − y − y1 = t − − t − 令 v=0,由(1)求得达最大高度 y2 时所用时间(t-20)=32,代入(2) t(s) F(N) 98 20 m1 m2 T' m1g a T' m2g a T T' T' 0.05 0.08 t(s) F(N) Fmax 0

第3章动量定理及其守恒定律习题解答 19 第3章动量定理及其守恒定律习题解答 中,得y2-y1=5030y2与ym=5030+1672=6702(m) 3.5.13抛物线形弯管的表面光滑,沿铅直轴以匀角速率转动,抛 设轨矩为l,外轨比内轨高h,有cosa=VP-h/1,sma=h1l 物线方程为y=x2,a为正常数,小环套于弯管上。(1)弯管角速度多 选图示坐标0-xy,对车箱应用牛顿第二定律: 大,小环可在管上任一位置相对弯管静止?(2)若为圆形光滑弯管, 情况如何? Ncosa=NVP-h2/1=mg①,Nsna=Nh/1=mv2/R② 解:以固定底座为参考系,设弯管的角速度 为ω,小环受力及运动情况如图示:α为小环处 ①②得:√P-h2/h=gR/v2,两边平方并整理,可求得h: 切线与x轴夹角,压力N与切线垂直,加速度 大小a=w2x,方向垂直指向y轴。 h=v211Vp+g2R2=69.42×1.4351N69.4+9.82×90002 在图示坐标下应用牛顿二定律的分量式: =0.0782m=7.8cm Ncos(90°-)=V sin a=mw2x① Nsin90°-a)=N cosa=mg ② 3.5.15汽车质量为1.2×10kN,在半径为100m的水平圆形弯道 上行驶,公路内外侧倾斜15°,沿公路取自然坐标,汽车运动学方 ①/②得:tga=w2x/g③:由数学知识:ga=dydx=2ax: 程为s-0.5t3+20t(m),自=5s开始匀速运动,问公路面作用于汽车与 所以,2m=o2x/g,o2=2ag,0=√2ag 前进方向垂直的摩擦力是由公路内侧指向外侧还是由外侧直向内 侧? 若弯管为半径为R的圆形,园方程为:x2+(R-yP=R,即 解:以地为参考系,把汽车视为质点,受力及运动情况如图示: (R-y)2=R2-x2,R-y=(R2-x2)2,y=R-(R2-x2)2 v=dsd=1.5t2+20,vl-5=1.5×52+20=57.5m/s,a=v2/R=57.521100=33 ga=/d=-(R2-x2)2.(-2x)=x/√R2-x 设摩擦力f方向指向外侧,取图示坐标。xy, 应用牛顿第二定律: 代入③中,得:x/WR2-x2=o2x1g,o=√g1WR2-x Ncosa+fsin a =mg Ncosa mg-fsin a ① Nsin a-f cosa ma a=159 3.5.14北京设有供实验用的高速列车环形铁 N sin a=man+f cosa② 路,回转半径为9km,将要建设的京沪列车时速 ②/①得:tga=(man+f cosa)(mg-fsna) 250kmh,若在环路上作此项列车实验且欲使铁 轨不受侧压力,外轨应比内轨高多少?设轨距 1.435m. mgtga-fsm atga=ma,+f cosa,f= n(giga-a.) cosa sin atga 解:以地为参考系,把车厢视为质点,受力 及运动情况如图示:车厢速度v=250km/h=69.4mls,加速度a=v2/R: gga-an=9.8tgl5°-33=-30.43<0,∴.f<0,说明摩擦力
第 3 章动量定理及其守恒定律习题解答 19 第 3 章动量定理及其守恒定律习题解答 中,得 y2-y1=5030 y2=ymax=5030+1672=6702(m) 3.5.13 抛物线形弯管的表面光滑,沿铅直轴以匀角速率转动,抛 物线方程为 y=ax 2,a 为正常数,小环套于弯管上。⑴弯管角速度多 大,小环可在管上任一位置相对弯管静止?⑵若为圆形光滑弯管, 情况如何? 解:以固定底座为参考系,设弯管的角速度 为ω,小环受力及运动情况如图示:α为小环处 切线与 x 轴夹角,压力 N 与切线垂直,加速度 大小 a=ω2x,方向垂直指向 y 轴。 在图示坐标下应用牛顿二定律的分量式: ② ① N N mg N N m x − = = − = = sin( 90 ) cos cos(90 ) sin 2 ①/②得:tgα=ω2x/g ③;由数学知识:tgα=dy/dx=2ax; 所以, 2ax x / g, 2ag, 2ag 2 2 = = = 若弯管为半径为 R 的圆形,圆方程为:x 2 + (R-y)2 = R2,即 2 2 1/ 2 2 2 2 1 2 2 2 2 2 1/ 2 2 2 1/ 2 / ( ) ( 2 ) / ( ) , ( ) , ( ) tg dy dx R x x x R x R y R x R y R x y R R x = = − − − = − − = − − = − = − − − 代入③中,得: 2 2 2 2 2 x / R − x = x / g, = g / R − x 3.5.14北京设有供实验用的高速列车环形铁 路,回转半径为 9km,将要建设的京沪列车时速 250km/h,若在环路上作此项列车实验且欲使铁 轨不受侧压力,外轨应比内轨高多少?设轨距 1.435m. 解:以地为参考系,把车厢视为质点,受力 及运动情况如图示:车厢速度 v=250km/h=69.4m/s,加速度 a=v2 /R; 设轨矩为 l,外轨比内轨高 h, 有 cos l h /l, sin h /l 2 2 = − = 选图示坐标 o-xy,对车箱应用牛顿第二定律: N cos = N l 2 − h 2 /l = mg ①,N sin = Nh/l = mv 2 / R ② ①/②得: 2 2 2 l − h / h = gR / v ,两边平方并整理,可求得 h: m cm h v l v g R 0.0782 7.8 / 69.4 1.435/ 69.4 9.8 9000 2 4 2 2 2 4 2 2 = = = + = + 3.5.15 汽车质量为 1.2×10kN,在半径为 100m 的水平圆形弯道 上行驶,公路内外侧倾斜 15°,沿公路取自然坐标,汽车运动学方 程为 s=0.5t3+20t (m),自 t=5s 开始匀速运动,问公路面作用于汽车与 前进方向垂直的摩擦力是由公路内侧指向外侧还是由外侧直向内 侧? 解:以地为参考系,把汽车视为质点,受力及运动情况如图示: v=ds/dt=1.5t2+20,v| t=5 =1.5×5 2+20=57.5m/s,an=v2 /R=57.52 /100=33 设摩擦力 f 方向指向外侧,取图示坐标 o-xy, 应用牛顿第二定律: ② ① sin cos sin cos cos sin cos sin N ma f N f ma N mg f N f mg n n = + − = = − + = ②/①得: tg (ma f cos)/(mg f sin ) = n + − tg m gtg a mgtg f tg ma f f n n cos sin ( ) sin cos , + − − = + = gtg − an = 9.8tg15 − 33 = −30.43 0, f 0 ,说明摩擦力 x y mg N a α ω x h l mg N y a α α y α x α=15° α f N an mg