
第五章 刚体力学基础 (一)刚体绕定轴转动运动的描述 力矩 一、填空、选择题: 1.二个恒定的力下1,F,(F,>F2)作用在一个可绕固定中心轴0转动的圆盘上,如图 (a),(b)所示,则二力对0轴的合力矩分别为: 就,赵(后一) M.=(Et)R 成,=x(且一) M=(上-E)R (a) (b) 2.刚体绕固定轴作匀加速转动,角加速度为B,初角速度为⊙o,则在刚体上离轴心为r 处一点在任一时刻的速率v三=YWt竹);切向加速度a=孕 ;法 向加速度4,=YCwo十,随时间变化的量是 山a'(o ③已知一刚体绕定轴转动的运动方程0=10+8t-5{则,02s肚,刚体的角速 度为6y风火;角加速度为 一10od少2,此的缅离.5显质点的 速度v=CW=3YS 加速度a邛+wF9找7m5 4.刚体以每分钟60转绕?轴正向作匀速转动。设这时刚体上一点P的位置矢量为 7=3了+4j+5灭,单位为“102m”,若以“10-2m·s1”为速度单位,则该时刻P点速度为 w=60x2T/60YW=2TY5( (A)v=94.21+125.6j+157.0派 7,二3+4 (B)v=-25.1i+18.8j (C)v=15.1i+18.87 v=元x (D)v=31.4j 5.一飞轮匀减速转动,在5s内角速度由40mrad·s1减到10mrad·s1,则飞轮在这5s 内总共转过了 625 圈,飞轮再经 167S 的时间才能停止转动: B=-30T二-6mr以52 二、计算题: 0二 40T-6方6 8:40Tt-3T62 L.如图所示,一条缆绳绕过定滑轮拉动升降机,滑轮半径r=0.5m,如果升降机从静止 ·13
第亟蕈 sll体力擎基础 (一 )刚 体绕定轴转动运动的描述 力矩 一、填空、选择题 : 1。 二个恒定的力 扌1∶ 九 (F1>毛 )作用在一个可绕固定中心轴 0转动的圆盘上 ,如 图 (a),(b)所 示,则二力对 o轴的合力矩分别为 : 砣a Ma=CF1十 F廴 )R 峪 砘 ˉ Mb=~LL二 hΣ艮___ △ (a) (b) 2.刚体绕固定轴作匀加速转动,角 加速度为 β,初 角速度为 ω0,贝刂在刚体上离轴心为 r 4.刚体以每分钟 ω 作匀速转动。设这时刚体上一点 P的位置矢量为 氵〓3i+4了 +5t,单位为 “102m” ,若 以“102m· s· ”为速度单位,则该时刻P点速度为: (A)氵 =%。 2氵 +125.6丁 +157.Ot (B)氵 〓-25.1氵 +I8。 8了 (C)氵 =15.1氵 +18.8氵 (D)氵 =31.4氵 5.一飞轮匀减速转动 ,在 5s内 角速度由娴πrad· s^l减 到 10πrad· s 内总共转过了 缸5 圈,飞轮再经 ∫、b7S _的时间才能停止转动。 四 =‘ 口Ⅸ △丌 尥 ° rWs=冫 丌 仫 钰 (趣 矿.¨ 3卩 十4矿 氵乙¢ס= 卩 二 一 曳 岁 工 、 -‘ 洱 r以 /t冫 一条缆绳绕过定滑轮拉动升降勰 豸廴石 ‘丌古 拶=+’π舌^3π 彳⒉ 歪r=O.5m,如 果升降机从静止 · 13· 5 ︱lIlⅤ 这 叼℃卯畹 J丶 !丬 冫丿κ ˉ "谬 二、计算题 : 1.如 图所示 , 处一点在1EE-时刻的速率 v=~」玺暨凵呷边|Ι切向加速 :℃ 逆 气 豇 「 港 向加 霎舅 即 〓」 午午华|邛匕庄— ,随 时间变化的量是 ( ˉ

开始以加速度a=0.4m·s2匀加速上升,求: (1)滑轮的角加速度; (2)开始上升后,t=5s末滑轮的角速度; (3)在5s内滑轮转过的圈数; (4)开始上升后,'=19末滑轮边缘上一点的加速度(假设绳与轮无相对滑动)。 ()B-冬=08rM52 (2) w=Bt=4-rad/ a ()日:是p6(0rd=人59国 (4)0=051 2上型体从静止开始以匀角加速度绕定轴转动,其角加速度为0,10d·。,试求从 开始转动后多少时间,刚体上一点的加速度与该点的速度成45°角?此时该点已转过的角 度是多少? w=5古 U=wr=βrt 光pr an=wr=e'rt? 1=4a0 6=月23.165 .14 0=工Bt205rad
开始以加速度 a〓 o.4m· s。 9匀 加速上升,求 : (1)滑轮的角加速度; (2)开始上升后,t△ 5s末滑轮的角速度; (3)在 5s内 滑轮转过的圈数; (4)开 始上升后,/=1s末滑轮边缘上一点的加速度(假设绳与轮无相对滑动)。 to肛 争=弘⒏rAd·/s亠 CV Gu=卩 名=4丫泓虍 c3’ σ二圭纱 饪 r口 洌 =火 轫 C4D Ⅱ =⒍J丨 讧谘 轴转动,其 角加速度为 0.10rad· s^2,试 求从 望苎望垫掣塾L笙Ξ豇 此叮 该点已转洋的 ? t/二 ∞r二 阝r古 即=钅钅纟|二 ″ εt.=△o⒎r=阝 ·r诌 2 饨 1ah= 协 艺| 、`b‘ ,、 r'^丿 匡 丨二 ’s' ⒉ ·· ,· L.. “川rˉ 〓'r `一 ·14· J= 亠

3.如图所示,发电机的皮带轮A被汽轮机的皮带轮B带动,A轮和B轮的半径分别为 1=30cm,2=75cm。已知汽轮机在启动后以匀角加速度0.8mrad·s2转动,两轮与皮带间 均无滑动, (1)经过多少时间后发电机的转速为600r/min,=2 oTra小 (2)当汽轮机停止工作后,发电机在1min内由600r/min减到300r/min,设减速过程是 均匀的,求角加速度及在这lmin内转过的圈数。C) g=2 SA=Sg =raee=3rBet? B ea=sretn W4= dea Ypet 6= 6 M Y6B C2)B-3加y%m2=-6Trdk2 8:+拉f462 三998d 4.有-一质量为m,长为1的均匀细棒,静止平放在滑动摩擦系数为4的桌面上,它可以 绕过其端点0且与桌面垂直的固定光滑轴转动,求摩擦力对0轴的力矩大小。 于:my f.f红 M=Jxof e ·15·
3.如图所示,发 电机的皮带轮 A被汽轮机的皮带轮 B带动,A轮和 B轮 的半径分别为 △〓3Ocm,、 〓75cm。 已知汽轮机在启动后以匀角加速度 0.8trad· s^2转动,两轮与皮带间 均无滑动, (1)经过多少时间后发电机的转速为600r/血n;一 冫口π n入‘杉色 (2)当汽轮机停止工作后,发 电机在 1而n内 由6∞r/血n减到 3∞r/血n,设减速过程是 绕过其端点 0且与桌面垂直的固定光滑轴转动 ,求摩擦力对 0轴的力矩大小。 :勹 的,求角加速度及在这 1∶ 蚤 内转过的圈数。cI乙 g:茔 阝:菇 冫 免彡5饣 〓q气 二圭r亻仫苦⒉ 弘=+←=/1卩:∮ %rJ △ 9ˉ ( 吩 铮 ′滗平瓦产 冖 = /口 s 卜艹 nv9您 · 罗 ⒈诤毵廴:龋 膏 L 6∶ - 雠 △迅:惑J皙任饪珐盏£静止i放在滑动摩擦系数为u的桌面上,它可以 ~篷≡垒≡基~→∝ J二 '爿 /· γn《笋 H/l=∶志斌 〃J孥 ~/夕纟竺望丝∠2匕 舀 呷 ∴圭旷 '切 饣 店 ξ2 ) ·15·

(二)转动定律 转动惯量 G=-元,不x0-3)0 一、填空、选择题: 1.下列各种说法、正确的是 xF+府0 CE 作用在刚体上的力越大,刚体转动角加速度越大; (B)作用在刚体上的力矩越大,刚体转动角速度越大; 瓜,=-成,机2-M23 (C)作用在刚体上的力对定轴的力矩越大,刚体绕该轴的角加速度越大: 心)作用在刚体上的合外力为零,刚体保持静止或匀角速转动: (E)作用力和反作用力对同一轴的力矩之和为零。 将一轻绳绕过一滑轮边缘,绳与滑轮之间无滑动,若()将重量为P的砝码挂在绳 端;(用一恒力F=P向下拉绳端,如图所示,分别用B,和B。表示两种情况下滑轮的角加 速度,则 (1)两滑轮所受九矩方向是 击有纸和向纳:滑轮转动方向为】 川顺时针 (2)B,和B,的关系是州双加纯hn花西 (A)B.>B (B)B.=Bb (C)B.<B (C)不能确定。 Ca) P-T=mua二mR TR-I8 ch)=P P p-专=mBR,2文+R ☑r (b) 3.一根均匀棒长L,质量m,可绕通过其一端且与其垂直的定轴在铅直面内自由转动, 开始时棒静止水平位置,它当自由下摆时,它的初角速度等于 ▣ ,初角 加速度等于 39 已知均匀棒对于通过其一端垂直于棒的转轴的转 2吧 动惯量为写nP。 I=登∫xx=专m2M=2 4.在半径为R的定滑轮上跨一细绳,绳的两端分别挂着质量为m,和m2的物体,且m1 >m2。 若滑轮的角加速度为B,则两侧绳中的张力分别为T,=m,(9-P) ,T2 m2(9tβ2 m1g-T=eRmI T-m2g=8Rm2 5.由2N根质量均为m的等长的匀质辐条和质量为M的匀质轮圈构成转轮,可绕垂直 于转轮平面并通过其中心的转轴转动,若将辐条数目减少为N根,又要保持转轮的转动惯 量不变,则轮圈质量应为 MBt me' .16 I轮MR2 F台p2与) 工瓶,根二子2 M'=mtim
-、 填空、选择题 : 冖 确 黛 磊骂蚨 ,毗转确 妞 (B)作用在刚体上的力矩越大,刚 体转动角 转动 惯 量 d×臼'讠 冫0。 (C)作用在刚体上的力对定轴的力矩越大,刚体绕该轴的角加速度越大; 粼霉舅犁筌趱鼷溴蠹懋 雩 转玑 L轻绳绕过一滑轮边缘 ,绳 与滑轮之间无滑动 ,若 (a)将 重量为 P的砝码挂在绳 端 丿(|褶角一恒力 F=P向下拉绳端,如 图所示 ,分别用 βa和 βb表示两种情况下滑轮的角加 d 律 一一 赧 丬砬 /:` 二 转 垧 赋 ;滑 轮转动方向为 "厥 lgi绀 ″绐〃△孑 (A)βa>β b (B)β a〓 βb ` ((亠 (C)β a(β b (C)刁 阝胄邕I,q矢 岜。 (A)βa>β b (B)β a〓 βb (C)β a(β b (C)不 能确定 L⑴ P-丁 :阻 =yh阝只 P cv卩 =【 3。 一根 P-∶ 均匀棒长言::∶J, ∶ii∶手差培;∶:端 叠与其垂直的定轴在铅直面内 自 1 r′ ` c⑴ P-丁:阻 =yh阝只 ÷卩i【 ∶i∶ rT:l叩 ⌒ P c厶 ’ 宀 自由转动, 开始时棒静止水平位置,它 当自由下摆时,它 的初角速度等于 ∷ , C9 ,初 角 加速度等于__.墨纭△____=丐 °已知均匀棒对于通过其一端垂直于棒的转轴的转 动惯量为合 m`。 工〓 召⒉£/∝切×:古 泗乇 ⒈ 胍 =弼 迓 4。 在半径为 R的定滑轮上跨一细绳,绳 的两端分别挂着质量为 m1和 m2的物体,且 m1 >m2。 若滑轮的角加速度为 β,则 两侧绳中的张力分别为 T1=讪 !(留 ˉ卩R, ,T2 叨 1J-Tl=`RⅡ勹 飞 u-阳 彳 z卩R〃h 2N根质量均为 m的等长的匀质辐条和质量为 M的匀质轮圈构成转轮 ,可 绕垂直 于转轮平面并通过其中心的转轴转动,若将辐条数 目减少为 N根 ,又 要倮持转轮的转动惯 ~0ˉ . , 力 ' 。 ' 量不变 ,则 轮圈质量应为 ·16。 触Rη 辔笋w扩 (⒍ Ι转训R冫 彡∥眸午管时) 工扌‰ 坊艮二 丁 ⒈ R么 W9朋巾瞥灬
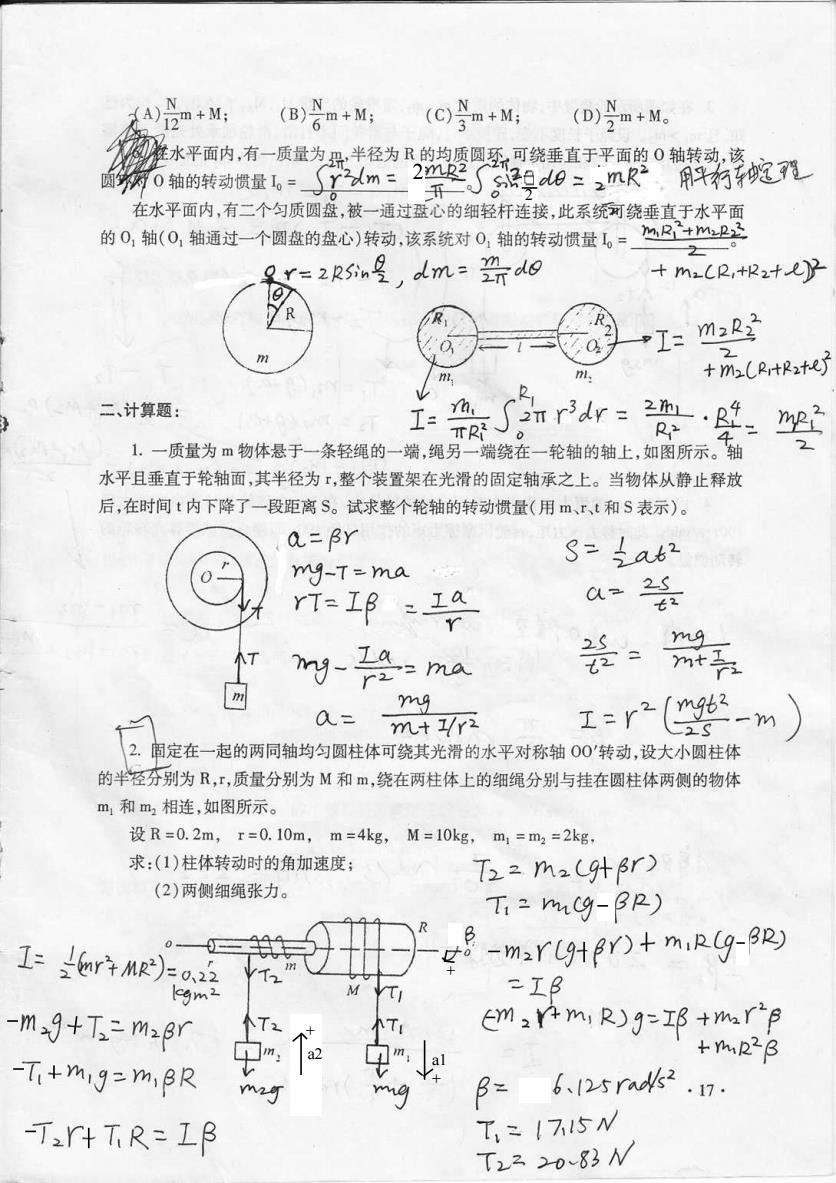
2m+M; (C)+ (D)分m+M。 继水平面内,有一质量为毋半径为R的均质圆至可绕垂直于平面的0轴转动,该 面0轴的转动惯量5:m:2兴96:,nR2 用柄婉羽 在水平面内,有二个匀质圆盘,被一通过盘心的细轻杆连接,此系统可绕垂直于水平面 的0,轴(0,轴通过一个圆盘的盘心)转动,该系统对0,轴的转动惯量L,:22+m卫子 2 ?r=2R50n号,dm=lg +m2Le,+e2+2 I= m2R> m 2 nl. +mCetezte 二、计算题: I= R> 1.一质量为m物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示。轴 水平且垂直于轮轴面,其半径为r,整个装置架在光滑的固定轴承之上。当物体从静止释放 后,在时间t内下降了一段距离S。试求整个轮轴的转动惯量(用m、r、t和S表示)。 a=βr S2a62 mg-T=ma YTeIβ-Ia a= 25 2 9 个T my-isma 七2 mg mt Iri 工=Y2( -m 2.固定在一起的两同轴均匀圆柱体可绕其光滑的水平对称轴00'转动,设大小圆柱体 的半径分别为R,r,质量分别为M和m,绕在两柱体上的细绳分别与挂在圆柱体两侧的物体 m和m2相连,如图所示。 设R=0.2m,r=0.10m,m=4kg,M=10kg,m,=m2=2kg 求:(1)柱体转动时的角加速度; T2h2(9外Br) (2)两侧细绳张力。 Ti=nucg-BP) 1:如r产m)=o.2 m.rcgter+mng-R 9m2 T 工B -m,9+T=m:8r T m,4m)9z6+mr月 +%22B -T+m9≥m,βR B=6、12ak2.17. -T.+TR=Lβ T之175W T22083W
〓B卩 ︱ ︱ ︱ ︱ ︱︱ ˉ ︱ 水平且垂直于轮轴面,其半径为 r,整个装置架在光滑的固定轴承之上。当物体从静止释放 后,在时间 t内 下降了一段距离 s。 试求整个轮轴的转动惯量(用 血、r、 t和 s表示)。 i⒍ 二阝r S=圭 '彡 ⒉ 叼 -t亠 hn~ ∷ Ct’ 亻“ rTˉ 工卩乙IL垒· 勹-;告箜|=阻 号荸|=钅擗 终 二 石镁彳万石Ⅰ ·二r⒉ C尖辔 堡一h 的I雪尝霸穿IB雀鳖暴蛋搭各帚 差罾桠篝奄钪帚荔Ⅰ m1和 m2相连,如 图所示。 衫乏R=0.2m, r〓 0。 IOm, m〓4kg, 求 :(1)柱体转动时的角加速度 ; (2)两侧细绳张力。 M〓 10kg, n1I=nb=2kg, ⒎2阳2Cg-阝r9 飞三%钐卞卩/a, L少孑 叨冫r印IF宀 一n:良 钐门′v T二 圭|Or冫 砘泛,〓 田、冫1 叻h亠 叩召厂L二 阳Σ卩r fIˉ /hIJ二 nI卩 R 飞r-TR=L卩 ` T` `″ , T【 `,, }丶 u百 γ a2 a1 + + + 2 2