
第十章 真空中的静电场 (一)库仑定律 电场强度 一、填空、选择题 1.真空中有两个点电荷M、N,相互作用力为下,当另一点电荷Q移近这两个点电荷时, M、N两点电荷之间的作用力F ‘C) (A)大小不变,方向改变 (B)大小改变,方向不变 (C)大小和方向都不变 (D)大小和方向都改变 2.下列几个说法中哪一个是正确的? (C) (A)电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向。十、一 (B)在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同。大小 C)场强方向可由E=下/q定出:其中g为试验电荷的电量,9可正、可负,下为试验电 08i 荷所受的电场力 月02a 85d (D)以上说法都不正确。 9个 4。C5 3.正方形的一对对角上,各置电荷Q,另一对对角上各置电荷q,若Q所受合力为零 则Q与g的大小关系为 af i (A)0-22g (B)Q=2q 4打.心 (C)Q=-4g (D)Q=24Q a→X : Q9月 4ngoa 4.一半径为a,电荷线密度为入的均带正电细园环,在环心处的电场强度E=O 若将圆环切掉长为△S的一小段,且a>△S,则环心处电场强度E的大小E= 入AS 方向 个Iro02 从环之AS 二0 二、计算题: Q=259 1,氢原子由一个质子和一个电子组成,根据经典模型,在正常状态下,电子绕核作圆 动,轨道半径r=5.29×10"m,已知电子带电q=-1.6×109C,质量m=9.11×10-"kg, 质子带电q=1.6×10-9C,质量M=1.67×10-”kg,万有引力常数G=6.67×10-"N·m2· kg2求: 国电子所受的库仑力,F。=22Y0》 2)库仑力是万有引力的多少倍, /hm二227X1o39 (31=3、63XoN】 (3)电子的速度。 Fe=mv ,v=z =2.l9xW0m/5 ·1
第十章 真空中的静电场 (一 )库 仑定律 电场强度 -、 填空、选择题 Ⅱ 1.真空中有两个点电荷M、 N,相 互作用力为f,当 另一点电荷 Q移近这两个'点 电荷时, M、 N两点电荷之间的作用力 f (A)大小不变,方 向改变 (C)大小和方向都不变 (6、 ) 11茗鹜瀵读露戈厶午景雪攫璧营廴电椅剜冫室该咖 场力的方向片、^(c) (B)在 以'点 电荷为中`b的 球面上 ,由 该点电荷所产生的场强处处赆 火热 x/C)场 强方向可由宦=氵q定 出;其 中q为试验电荷的电量,q可 正、可负,扌 为试验电 (B)大小改变 ,方 向不变 (D)大小和方向都改变 淅受的畅九 Ψ ^、 (D)以上说法都不正确 二 ℃ 甫 「盏 君 轹 段 ,各 置电黢 苷戈一缶缶诌i 孑 黼 二各置串荷 q1若 Q所受息力 曰 Q与 q爱大小 ¥ 为 孔沩 产冖冖 丐歹矿 攵 十 可 =吒 ”砬(A)丿 谜 ~£卜¨Ξh 叩=-Ξ 1j1{《 /fL {笋Li2∶L-∶ |引 l∶ ∶ ∶ ij1廿 猃 耘 ir 丕 LⅡ L篝 ‰ ;i 轷叮也£ 4,一半径为 a,电 荷线密度为 λ的均刃释正电绅园 .环 , )处 的电场强度E= 口 l} ' 玩叠赢蔹森缶L锪Ⅰ正『瓦森£荔菇f雾真il=缵α =蔫 薯 ≡ 军 J凫 态 王 卿 °处 吧 物 强 度 L田 人 盱 _咩 彡 0丿 二、计算题 : 1.氢 原子由一个质子和一个电子组成 ,根据经典模笛 ,在 正查状态下 ,电 子绕核作圆9='彩 动 ,轨道半径 r=5.⒛ ×101lm,已 知电子带电 q=-1.6× 1019C,质 量 m=9.11× 1031炖 , 质子带电 q=1,6× 10I9C,质量 M=1.臼 ×1027kg,万有引力常数 G=6,臼 ×10Ⅱ N· m2· 吒 2求 : r3l电 ∷|霪云 子 雾 的速 鼋 度 碧霉。 拿;乩室ri等f钅扌⒎FL辶、:;;f∶饣 c卢即二 re=箐乒∶ 、v二 熏 =⒉ "x/口 沙Ⅱ芯 3、 ‘3×`J句 ˇ’ ·1·

有两个等量的点电荷,相距2,分别带电+Q,在这两个点电荷连线的垂直平分线 有最大场强的点的位置。 E-风 ·9·2= Q 烈n但 H4atr) snGoa 1ttgo =仅 2, a+v21 2T%,0心 sing losg 仅co39 de dE-0 之么a 。。 2590co59) )9=t正 号 C09= 3.一均匀带电环形平面板,电荷面密度为σ,内外半径分别为R1,R2,求轴线上任一点 的电场强度。 万法1: dE=xda 之X2m46 +.c4y)月 4r.CX年r2)月 E-Rsror 户) 2知 方法正:补偿法 4.电荷q均匀分布在半径为R的半圆周上,求圆心0处的电场强度 入dL= idg TR T dE- d qdo 4n4R 4ntoR' dEx二dEsn9,lEy=dEo9 点=∫x-∫Es6=g2 &n9d8 2 2T22R2 ) .5与,产aa 0 2T22
△ 有两个等量的点 电荷 ,相 距 2a,分 别带电 +Q,在 这两个点 电荷连线 的垂直平分线 有最大场强的点的位置。 汪 爿卜夕 亠Ⅱ%旷 lˇ″ s丿 h陲 峋 f二 ·叉J· 2二 =靳 Ⅱ弘 ` , ≥ 丿 少厂 钅 葶 笠⊥£∞扌乡 |二 夕 2‘hρ ω“ 彐二±晷势 。 =土 吾 厶s9亠 ∠孑⒎ rˉ ± 3.一 均匀带电环形平面板,电 荷纛面密度为 叱 酚 半径分别为 民 凡 求轴线上任一点 △ 阢 阢 的电场强度。 戋讠么ェ:翔舷 讠女 4.电 荷 q均匀分布在半径为 R的半圆周上 ,求 圆心 0处 的电场强度: 勿丌一 9茄矽 钿 △ R亠 工 丬 苈运= z E诋卜蚤 群协 L铮啸 一÷轰雨了) 沈乡=λ 茄彡=孑早仁「 ·Rdρ = 以叵: :型立冖= 钿 %r 涩气 二另庄ζh汐 '丿 %勿 汇 夕$ρ ‰ 讠 J》E× =f茄 Eζ`'ˉ 兔 ‰ 峨 伊茄汐 =彐 匚 一 %羽 ε冫 二r轹 湫 吻 犭 气旷 苣=毳 彡 丿 ·2·
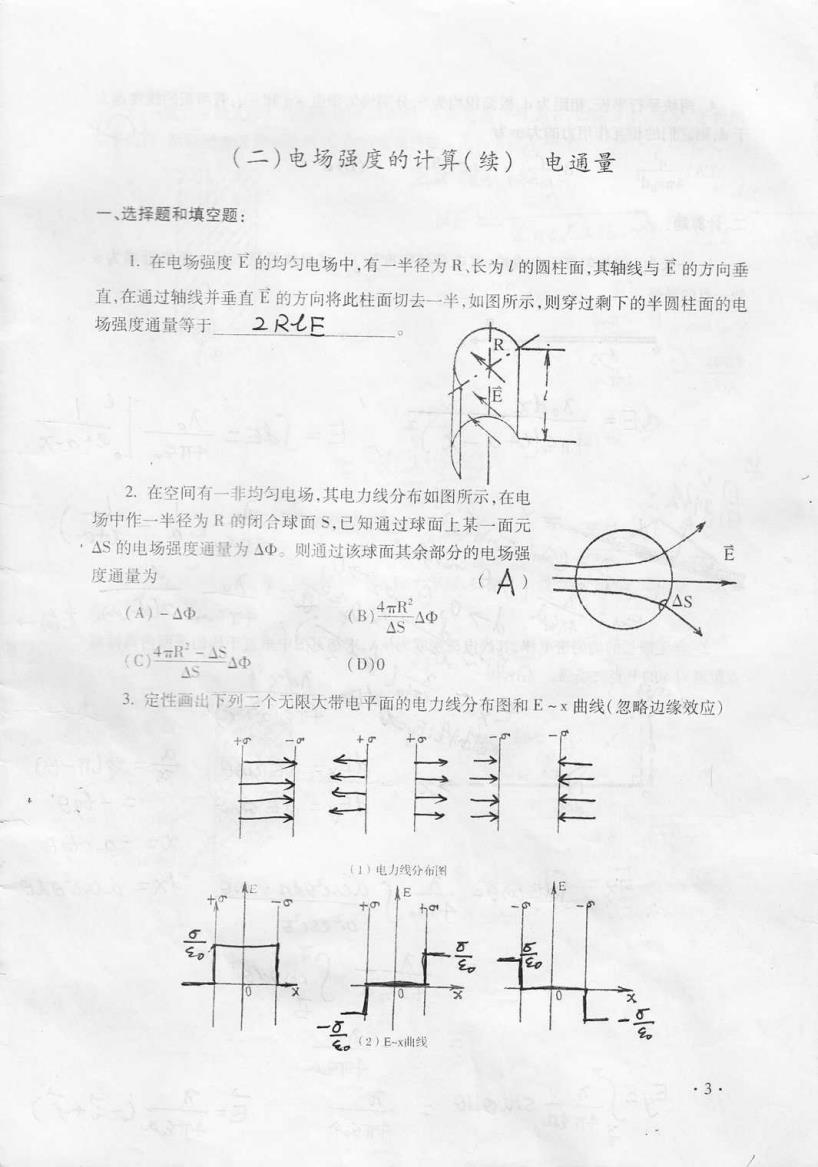
(二)电场强度的计算(续) 电通量 一、选择题和填空题: 1.在电场强度E的均匀电场中,有一半径为R,长为1的圆柱面,其轴线与E的方向垂 直,在通过轴线并垂直E的方向将此柱面切去一半,如图所示,则穿过剩下的半圆柱面的电 场强度通量等于 2R七E 2.在空间有一非均匀电场,其电力线分布如图所示,在电 场中作一半径为R的闭合球面、,已知通过球面上某一面元 ·AS的电场强度通量为△④。则通过该球面其余部分的电场强 度通量为 (A) (A)-△电 (B)4R: As Ap (C4R中 49 (D)0 3.定性画出下列二个无限大带电平面的电力线分布图和E~x曲线(忽略边缘效应) 居目 (1)电力线分布图 。(2)E-x曲线 ·3·
(二 )电 场强度的计算(续 ) 电通量 一、选择题和填空题 : 1.在电场强度 宦的均匀电场中,有 工半径为 R、 长为 J的 圆柱面,其轴线与 宦的方向垂 直,在通过轴线并垂直 宦的方向将此柱面切去一半,如 图所示,则 穿过剩下的半圆柱面的电 场强度通量等于 2M ⊥ 。 2.在空间有一非均匀电场 ,其 电力线分布如图所示 ,在 电 场中作∵半径为 R的闭合球面 s,已 知通过球面上某∵面元 ΔS的 电场强度通量为 ΔΦ。则通过该球面其余部分的电场强 度通量为 (A)-ΔΦ ∝ )TΔ Φ cA) ∷ ⑶譬Δ⒍∷ Ⅰ (D)O Ⅱ 3.定性画出T刃=个无限大带电平 田的电力线分布图和 E· x曲线(忽 略边缘效应) +。i -σ % 〈2)E~x lll线 3·

4.两块平行平板,相距为d,板面积均为$,分别均匀带电+q和-q,若两板的线度远大 于d,则它们的相互作用力的大小为 Q (B) (D) 二、计算题: 1.一长为1的均匀带正电线段,其电荷线密度为入。,试求线段延长线上距离近端为: 处一点的场强。 0 o inrax)fle dE=xodx Ex行a(589,8) 2c女) 4灯w d>0,9,9201 2。 4r0 N比t 方向→ 2半无限长的的匀带电背彩数零免中套直于花的平面内离修端 点距离为的P点之场强。 ndx 19 10、 4T4a'+x) dEx=dEiose =i-) 之x dEy=dESino 2-9 X:actg日 5=E9:a∫ag dX-acst2台lB a"esc 4T为a cosodle 马 入 4T4oa 4 sin9dg 7 4折 4π0 )
ˉ 4,两块平行平板,相距为 d,板面积均为 s,分别均匀带电 +q和 -q,若两板的线度远大 (a 于 d,则 它们的相互作用力的大小为 (A〕蒂 ⑶檗 ⑹淼 (叻 ∞ 二、计算题 : 1.一长为 J的均匀带正电线段 ,其 电荷线密度为 λ。,试 求线段延长线上距离近端为 a 处一点的场强。 o〓==弓 ΞΞF〓 ==〓l=Π「==ˉ ·x 浃 吲 骺 π '卜 夕 E二 括 |‰ 半 ^∶ ` =^兮飞Tc÷ -捃) ˉ 括 玄台瓦石龋→ 2.半无蘑甏钒均匀带电棒 ,亳彳 砰隅悉叮丫 邕于棒的平面内离棒端 泅?刀o1 T【 刁 名 舱帚猁 t~=卩 阝 '¨握. 舀{ ‰ { +λ 洗Ξx二 仄L铋 ε 各 =勾 GTT~钐D 9 J两 ◆ × =d巨 空叼ρ 二ˉ勺ρ ~ 氧=p匚溯二 =^⒍ 轳ρ =阜 瓦J兰竺鱼皇型鲎ェ卫2⒐ 刃x=^“‘ Ξ矽沾 ` 汪⒉“幽 1犭辐 夕诏淝 9 轱 sI四膨 舡^ 二轱 苣〓‰ 乙-扌t力 ·4·
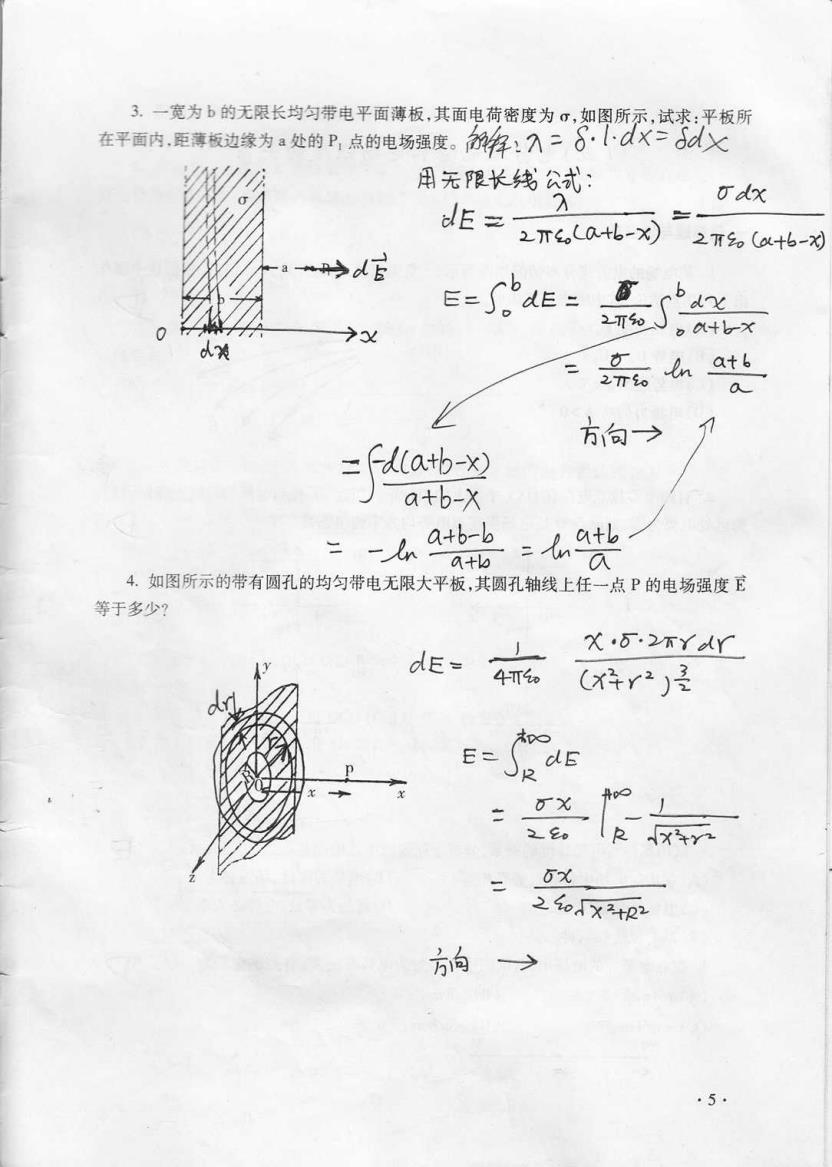
3.一宽为b的无限长均匀带电平面薄板,其面电荷密度为σ,如图所示,试求:平板所 在平面内,距薄板边缘为a处的P,点的电场强度。解1入二6·卜dX>火 用无限长线公式: odx dE之 2T,C0+6-x) 2T0(x+6-习 an→dG x 。+。X 2T0 方向之 7 a a+b-X a+b-b 4.如图所示的带有圆孔的均匀带电无限大平板,其圆孔轴线上任一点P的电场强度E 等于多少? X5·2不Y以Y dE= 4T切 (4×2)3 -u 二 20x2+22 5
3.一 宽为 b的无限长均 匀带电平面薄板 ,其 面电荷密 雩芒 罗 啻 :旱 ′ 殷 --R∶LⅠ萝 所 在平画内。距薄板边缘为 a处 的 Pl点 的电场强度。汤钐络t彡 囝元限长线 父忒l 歹灰× 丿E= 9 △丌C,匕+L书o 之T‰ Cpt+1'V 廴 轱 厶 芈 E二 r岁庆Ξ二 … 丁 0F?// 4.如 图所示的带有圆孔的均匀带电无限大平板,其 圆孔轴线上任一点 P的 电场强度 宦 等于多少? ∝ ·y· 冫π丫以r C'r△ r⒉ 丿|釜 匕么 绯争二钅辔 丿Eˉ 丐石丰万∷ E二 JF⒈ε =歹x丨孓抟弓Γ 之 亻。丬λ7ψ⒉ 责尚 → ·5·