
第十一章恒定电流的磁场 44e (一)磁感应强度毕一萨定律及应用 一、选择题与填空题: 1.一圆电流在其环绕的平面内所包围区域各点的磁感应强度阝: (A)方向相同,大小相等; (B)方向不同,大小不等: (C)方向相同,大小不等: (D)方向不同,大小相等。 2.电流由长直导线流人一电阻均匀分布的金属矩形柜架,再从长直导线流出,设图中 0、02、0处的磁感应强度为1,B2,B,则: (A)B1=B2=B2=0 (B)B1=2=0,B,≠0 (C)B1=0,B2≠0,B,=0 (D)B1=0,B2≠0,B3≠0 02 03 3.边长为L的一个导体方框上通有电流I,则此框中心的磁感应强度 (A)与L无关; (B)正比于L2; (C)与L成正比; (D)与L成反比 (E)与P有关。 4.如图两个半径为R的相同的金属环在a、b两点接触(a、b连线为环直径),并相互垂 直放置,电流I由a端流人,b端流出,则环中心0点的磁感应强度大小为: (A) (A)0 (B) 4R o验 ·16:
第:十 ˉ章∷∷恒定屯`流∷的磁场 毕ˉ萨定 ∷ 律及应用 1.一 圆电流在其环绕的平面内各点的磁感应强度 茁: (A)方 向相同,大小相等; ∷ (B)方 向不同,大小不等; ∷∶∷.∷ (C)方 向相同,大小不等; Ⅱ ∶ (D)方 向不同,大小相等。 2.电 流由长直导线流人一电阻均匀分布的金属矩形柜架,再从长直导线流出,设 图中 ˉ · ·ˉˉˉˉˉ |∶ ∶∶∶∶∶∶∶∶∶∶∶||ˉ ˉ ,.· ˉ 厂 ˉˉ ~ Ⅰ~I~ ェ 3.边长为 L的∷个导体方框上通有电流 I,则此框中心的磁感应强度 ∷ (A)与 L无关; (B)正 比于 ′; (C)与 L成正比; (D)与 L成反比 (E)与 ′有关。 4.如 图两个半径为 R的相同的金属环在 a、 b两点接触 帚 径 ),牙 谔屑 直放置 ,电 流 I由 a端流人 ,b端流出,则环中心 0点 的磁感压 莺 (一 )磁 感应强 j度 一、选择题与填空题: 01、 02、 03处的磁感应强度为j1j2j3,贝刂: (A)B1亠 B2〓 B3=0 (C)B1〓 0, B2≠ 0, B3=o (A)0 (B)措 泅架 ⑼譬 (B)j1亠 Bz=0, 言3≠ o (D疒言1〓 盯瓦乒0,言3≠ o C○ (~∶ !;丨 ) (~!∶ ))) ·16·
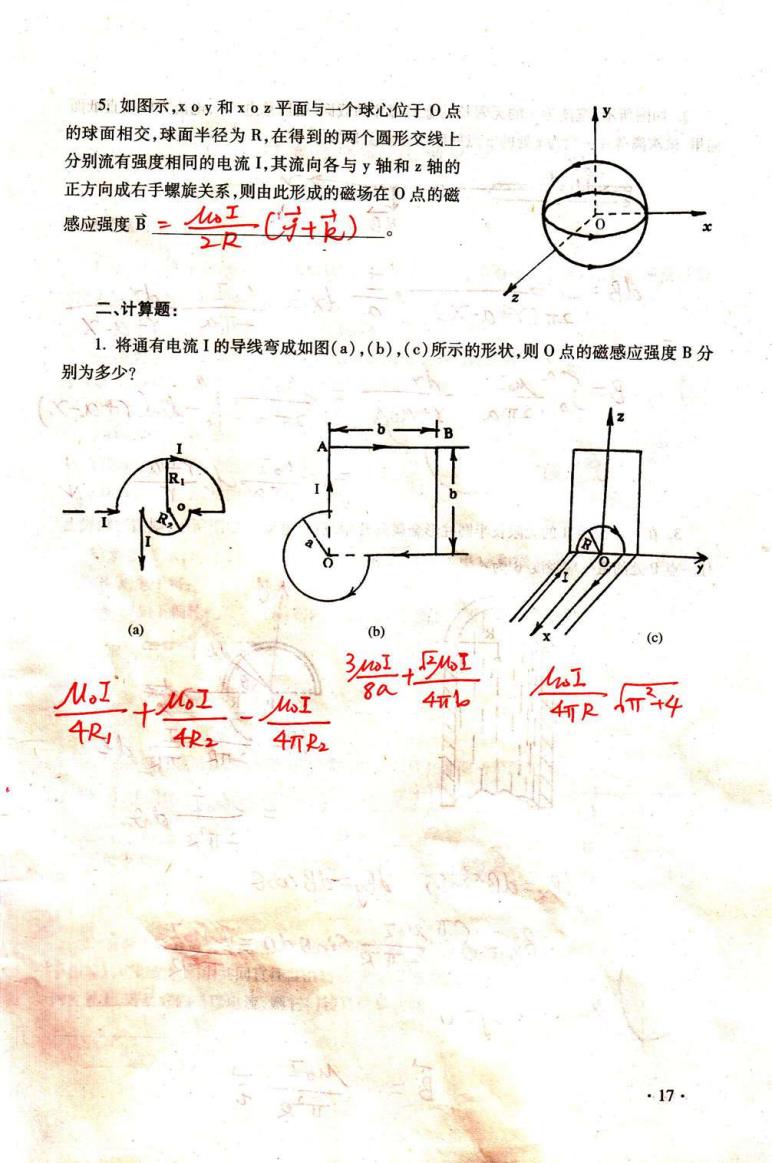
5.如图示,x0y和x0z平面与一个球心位于0点 y 的球面相交,球面半径为R,在得到的两个圆形交线上 离水女果 分别流有强度相同的电流I,其流向各与y轴和z轴的 正方向成右手螺旋关系,则由此形成的磁场在O点的磁 感应强度B二(时+) 二、计算题: 1. 将通有电流I的导线弯成如图(a),(b),(c)所示的形状,则0点的磁感应强度B分 别为多少? B (b) (c) W.1 M 4m6 何尺行+4 4机P2 ·17
∷Ⅱ玎∵如图示,x∶ 9i和 xo'平面与△个球心位∷于ρ点 的球面相交,球面半径为R,在得到的两个圆∷形交线上 分别海有强度相同的电流I,其 流向各与∮轴釉立轴的 正方向成右手螺旋苯系,则 由此形成的磁场在p点的磁 蒽应娘度∷j三 型丝墨三E星⊥宝‘ 、∷∵ ˉ 二、计算题: ∷ ∴ ∴Ι r 1.将通有电流I的导线弯成如图(a),(b),(c)所示的形状,则 o点 的磁感应强度 B分 别为多少? ∶ =△∴∷ ● , 彡”Ⅱ工∷ 衍 :厶 爹啭 而 迦 篑∷ ∶ :唣 。 : iF夂 ∷ 钶 肛 · `.∷ ' 7∶|亨∶蚤了0 ∷Ⅱ .Ⅱ ∶∶∶i∷ ∶∶:皂熏营宫壬:|∶ 17·

2.如图所示,宽度为a的无限长的金属薄片的截面,通以总电流I,电流方向垂直纸面 向里,试求离薄片一端为r处的P点的磁感应强度B为: 加交群面总国 【张中的同出林端设 能,关道学年计英词面 》一是童明 8ax吾k 以 2兀& Yta-x B=01 会点Crta刘 领以↓ 3.在一半径为R的无限长半圆柱形金属薄片中,通有电流I,如图所示,则圆柱轴线上 任一点P处的磁感应强度B为: R 8 最最北 .工dd 2切次 dB=desine,My-dBo Bx7m90= T22 By-o ·18·
2.如 图所示,宽度为 a的无限长的金属薄片的截面j通 以总电流 I,电 流方向垂直纸面 向里,试求离薄片△端为r处 的p点 的磁感应强度 B为△∷∶∶△∷ Ⅱ == ∷·∷¨ 0 9-∵ ∷ 沈B I∷ ∷ ∶ 1∷ェ :∷ ∷ △ ∷ 忄 豸冗瓦Γ ·丢加·z壅~丛辶 ∷ Dcta rt犹 △刃 旰觅旰 缶 F绎h汛而 ∷ △《箅知毛厶 :辱⒐ ↓ 3.在△半径为 R的无限长半圆柱形金属薄片中,通有电流 I,如 图所示,则 圆柱轴线上 任工点P处的磁感应强度言为: 刃£妊:柔 加 吖篝桫 ·18· 茄民=仄B臼昭'钧 叫 罕冖 0 民ˉ¢纬 。Ⅱ F禽 刊氵彡o 3亠 ∠吐~刂 丨1\∶ 刂∵

单洋甘聊轮华部流提否出视发香由甚格医静游的单饭国: 单将膏 费酒 (二)毕一萨定律应用(续)、高斯定理 一、选择题与填空题 1.四条相互平行的载流长直导线,电流强度均为L,且垂直于纸面,如图放置,正方形的 边长为2a,则正方形中心0的磁感应强度应为: ‘○ (A)B=21 Ta (B)B=24 02a (C)B=0 00 (D)B=1 2.一卉口曲面如图,开口是半径为R的圆,匀强磁场B与开口圆所决定平面的内法线 方向的夹角为0,通过这个曲面的磁通量为 (A)0 (B)-TR2Bcos0 (C)πR2Bcos0 (D)TR Bsin0 3.如图有六根无限长导线互相绝缘,通过电流均为L,区域I、Ⅱ、Ⅲ、Ⅳ均为面积相等 的正方形,问: 事资,书长闻,P庆开折泌生过 个 个 :、,应端收法和,火演国进明心示品减少的 2 之-。一A(逃礼两开代 :是分中慰酒《S (A)通过区域 工V的磁通量为零。 A (B)通过区域亚指向纸外的磁通量最大。 (C)通过区域立指向纸内的磁通量最大。 4. 电量为q的带电粒子以角速度ω作半径为R的匀速率圆运动,在圆心处产生的磁 感应强度B= 九。w .12 杯P
∷∷ ∷∷∷∷∷∴∷∵∷∷ 0Ⅱ∷ ∷∷△∷ ∷∶ ∷Ⅱ∷ ∷∵∷△~ ∴∷ ∷ ∷言: ∷ Ⅱ亭 ∵ `l (二)毕 ∵萨定律应用(续 )(高 斯∴定理: -t选择题与填空题: 1.四条相互平行的载流长直导线,电流强度均为I,且垂直于纸面,如 图放置,正方形的 边长为 za,贝刂正方形中心 o的磁感应强度应为: (D (A)B〓 ⒉型L1 πa 山:|篇 ∷ 、| (C)B_o ∷ . ∷ = ^ ` ∷ .∷ ∷Ⅱ∷∶∶ |i∴ ∷∴∷ ∷∶∶ ∶ = 早:虍呷 乌 (A)0 (B)亠 πR2Boosθ (C)πR2Bcosθ (o)π |口 R2Bsinθ 早咛肀艺 3.如图有六根无限长导线互相绝缘,通 过电流均为 I,区域 I、 Ⅱ、Ⅲ、Ⅳ均为面积相等 的正方彤,问 Ⅱ ∷ Ⅱ∶∷ˉ∷∴∵∷∵Ⅱ ∵Ⅱ `;: (^)通过区域 △ J/m磁通量为氛 ˉ i| 彗最大。 啻最大。 半径为 R的匀速率圆运动,在 圆心处产生的磁

才5. 半径为R的细圆环均匀带电,电荷线密度为入,若圆环以角速度。绕通过环心并垂 直于环面的轴匀速转动,则环心处的磁感应强度B。二子轴线上任一点的磁感应强度 B= 从R3 2C须+x万 年讲丝州而泸证 二、计算题和证明题: 1.如图所示,载流无限长直导线电流【,与直线共面的矩形面积和三角形面积的磁通量 分别为多少?于 a) b 6 a ←a I cb-am) 其距四密细 2.两根长直导线沿半径方向连接到粗细均匀的铝环上A、C两点,导线的另外两端与很 远的电源相连接,试证明“无论A、C两点在圆环上何处,环心O处的磁感应强度恒为零。 I14=12 0- 工 Ri ® B2:o12 4πk2 ⊙ B32B430 B20 ·13·
卜 半径为 R的细圆环均匀带电,电荷线密度为λ,若 圆环以角速度 0绕通过环心并垂 面的轴匀速转动,则 环心处的磁枣瘅弭擘 ∷Bo△圭2口步狲线上任=点的磁感应强度 0〓~ ∴ ∷∷∷ ∷ ∷∷ ∵ 氢线共面的矩形面积和三角形面积的磁通量 - ∶△ · \~⊥ Ⅱ ∵∷ ∷「l|∷ △ 耔十?丿 ∷Ⅱ∵ ∷ 均匀的铝环上 A、 C两点,导线的另外两端与很 l环上何处,环心 0处的磁感应强度恒为零。 冫/o工∷记 (∶ ∶∶∷茹 T疝廴 9t+L ~∶|π 卜 七 .=Ⅱ “ Ⅱ沙昔。 主rˉeI二 ェP以,∴ ∷ 即钎年 @ B冫 ~'饨 王∷∶ˉe. +T托冫 B3亠 ‰二刁 B¨ 0 ·13·