
第10章波动习题解答 68 第10章波动习题解答 第十章波动基本知识小结 10.2.1频率在20至20000Hz的弹性波能使人耳产生听到声音的 感觉。0°C时,空气中的声速为331.5m/s,求这两种频率声波的波长. 1.平面简谐波方程y=Acos@(t干)=Acos(ot干k): 解:V=v元,∴.元=V/,1=V1y=0≈16.58m oT=2π,k1=2π,v=1/T,V=v. 12=V1y2=331.5/20≈16.58×10-3m 2弹性波的波速仅取决媒质性质:弹性体中横波的波速 V=√NIp,弹性体中纵波的波速V=√TIp,流体中纵波波速 10.2.2一平面简谐声波的振幅A=0.001m,频率为1483Hz,在 20°C的水中传播,写出其波方程。 V=√kIp,绳波波速V=√TIp。 解:查表可知,波在20°C的水中传播,其波速V=1483ms.设 0-x轴沿波传播方向,x表示各体元平衡位置坐标,y表示各体元相 对平衡位置的位移,并取原点处体元的初相为零,则: 3.波的平均能量密度£=po2A2,波的平均能流密度 y=Acos2π(t-)=0.001c0s(2966πt-2πx) 1=p02A2V. 4波由波密射向波疏媒质,在边界处,反射波与入射波相位相 10.2.3已知平面简谐波的振幅A=0.1cm,波长1m周期为102s, 同:波由波疏射向波密媒质,在边界处,反射波比入射波相位落后 写出波方程(最简形式).又距波源9m和10m两波面上的相位差是 π,相当损失半个波长:例如:在自由端无半波损失,在固定端有 多少? 半波损失。 解:取坐标原点处体元初相为零,ox轴沿波传播方向,则波方 5振动方向相同、频率相同、位相差恒定的二列波叫相干波, 程的最简形式为 相干波叠加叫波的干涉。 6振幅相同、传播方向相反的两列相干波叠加产生驻波现象: y=Acos(t-)=Ac0s2π(片-)=10-3cos2π(1001-x) 驻波方程y=2Ac0s三x cosot:波节两边质元振动相位相反,两 △Φ=2π(1001-9)-2π(1001-10)=2π 个波节之间质元振动相位相同:相邻波节或相邻波腹间距离为入2, 相邻波腹波节间距离为入4。 10.2.4写出振幅为A,频率1=f,波速为V=C,沿o-x轴正向传播的 7多普勒公式:=学v,在运用此公式时,以波速V为正方 平面简谐波方程波源在原点。,且当=0时,波源的振动状态是位移 为零,速度沿o-x轴正方向。 向,从而确定Vo、Vs的正负。 解:设波源振动方程为y=Acos(o1+中)
第10章波动习题解答 68 第10章波动习题解答 第十章波动基本知识小结 ⒈平面简谐波方程 y Acos (t ) Acos( t kx) V x = = ; T = 2, k = 2, v = 1/T, V = v 。 ⒉弹性波的波速仅取决媒质性质:弹性体中横波的波速 V = N / ,弹性体中纵波的波速 V = Y / ,流体中纵波波速 V = k / ,绳波波速 V = T / 。 ⒊波的平均能量密度 2 2 2 1 = A ,波的平均能流密度 I A V 2 2 2 1 = 。 ⒋波由波密射向波疏媒质,在边界处,反射波与入射波相位相 同;波由波疏射向波密媒质,在边界处,反射波比入射波相位落后 π,相当损失半个波长;例如:在自由端无半波损失,在固定端有 半波损失。 ⒌振动方向相同、频率相同、位相差恒定的二列波叫相干波, 相干波叠加叫波的干涉。 ⒍振幅相同、传播方向相反的两列相干波叠加产生驻波现象; 驻波方程 y A x t 2 cos cos 2 = ;波节两边质元振动相位相反,两 个波节之间质元振动相位相同;相邻波节或相邻波腹间距离为λ/2, 相邻波腹波节间距离为λ/4。 ⒎多普勒公式: v v V VS V V − − = 0 ' ,在运用此公式时,以波速 V 为正方 向,从而确定 V0、VS的正负。 10.2.1 频率在20至20000Hz的弹性波能使人耳产生听到声音的 感觉。0ºC 时,空气中的声速为 331.5m/s,求这两种频率声波的波长。 解: V = v, =V / v, 1=V / v1 = 331 20 .5 16.58m V v m 3 2 / 2 331.5/ 20 16.58 10− = = 10.2.2 一平面简谐声波的振幅 A=0.001m,频率为 1483Hz,在 20ºC 的水中传播,写出其波方程。 解:查表可知,波在 20ºC 的水中传播,其波速 V=1483m/s.设 o-x 轴沿波传播方向,x 表示各体元平衡位置坐标,y 表示各体元相 对平衡位置的位移,并取原点处体元的初相为零,则: y Acos2 v(t ) 0.001cos(2966 t 2 x) V x = − = − 10.2.3 已知平面简谐波的振幅 A=0.1cm,波长 1m,周期为 10-2 s, 写出波方程(最简形式).又距波源 9m 和 10m 两波面上的相位差是 多少? 解:取坐标原点处体元初相为零,o-x 轴沿波传播方向,则波方 程的最简形式为 cos ( ) cos 2 ( ) 10 cos 2 (100 ) 3 y A t A t x x T t V x = − = − = − − = 2 (100t − 9) − 2 (100t −10) = 2 10.2.4 写出振幅为 A,频率 v=f,波速为 V=C,沿 o-x 轴正向传播的 平面简谐波方程.波源在原点 o,且当 t=0 时,波源的振动状态是位移 为零,速度沿 o-x 轴正方向。 解:设波源振动方程为 y = Acos(t +)
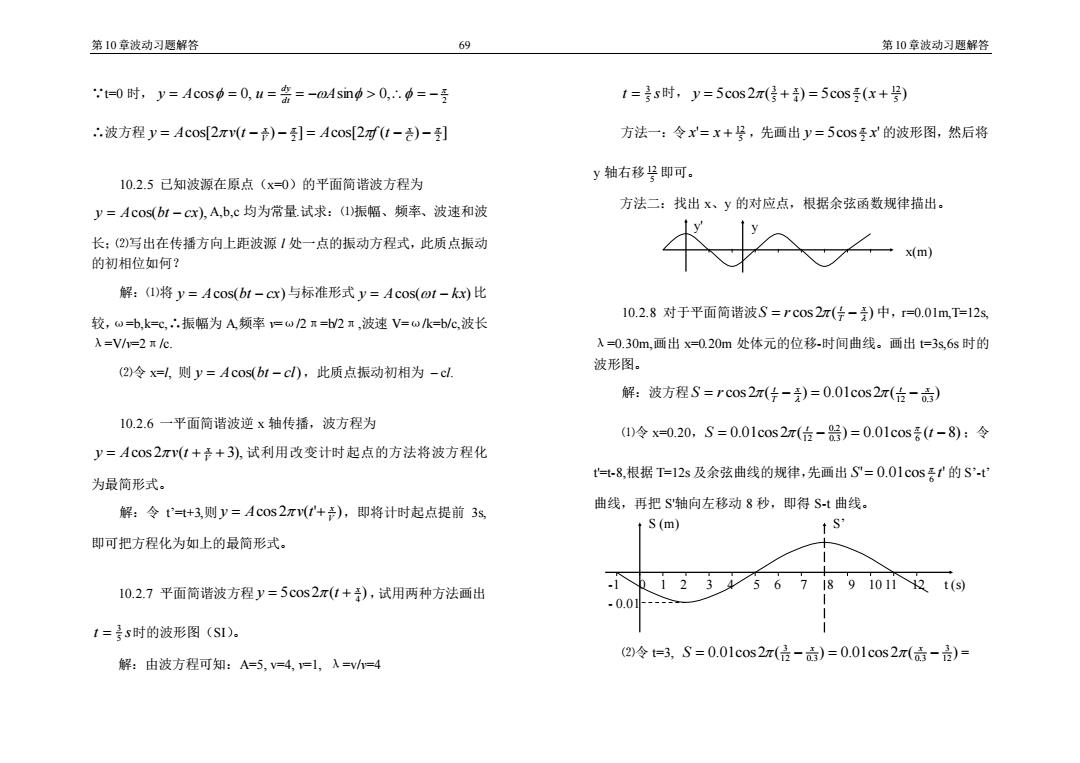
第10章波动习题解答 69 第10章波动习题解答 t=0时,y=Acos=0,u=斋=-Asmp>0,p=-号 1=s时,y=5c0s2π(是+)=5cos号(x+号) .波方程y=Ac0s[2πv(t-)-]=Acos2四(t-)-] 方法一:令x=x+竖,先画出y=5cos马x的波形图,然后将 y轴右移是即可。 10.2.5已知波源在原点(x=0)的平面简谐波方程为 y=Acos(bi-cx,A,b,c均为常量试求:(I)振幅、频率、波速和波 方法二:找出x、y的对应点,根据余弦函数规律描出。 长:(2)写出在传播方向上距波源1处一点的振动方程式,此质点振动 x(m) 的初相位如何? 解:(I)将y=Acos(bt-cx)与标准形式y=Acos(o1-kx)比 10.2.8对于平面简谐波S=rcos2π(片-)中,=0.01m,T=12s, 较,0=b,k=℃,.振幅为A频率=w2n=b/2π,波速V=wk=b/C,波长 λ=V/h=2ne. 入=0.30m,画出x=0.20m处体元的位移-时间曲线。画出t=3s,6s时的 (2)令x=l,则y=Acos(bt-cl),此质点振动初相为-cl. 波形图。 解:波方程S=rcos2π(片-)=0.01cos2π(位-高) 10.2.6一平面简谐波逆x轴传播,波方程为 (1)令x=0.20,S=0.01cos2π(5-船)=0.01cos号(t-8):令 y=Acos2πv(t+产+3),试利用改变计时起点的方法将波方程化 t=t-8,根据T=12s及余弦曲线的规律,先画出S=0.01cos妥1'的S-t 为最简形式。 曲线,再把$轴向左移动8秒,即得St曲线。 解:令t°=t+3,则y=Acos2π(t+),即将计时起点提前3s S(m) ↑S 即可把方程化为如上的最简形式。 11234 67i8910112t(s) 5 10.2.7平面简谐波方程y=5cos2π(t+),试用两种方法画出 -0.01- 1=号s时的波形图(SI)。 解:由波方程可知:A=5,=4,1=1,入=vh=4 (2)冷t=3,S=0.01cos2π(倍-高)=0.01cos2π(债-)=
第10章波动习题解答 69 第10章波动习题解答 ∵t=0 时, 2 cos 0, sin 0, y = A = u = = −A = − dt dy ∴波方程 cos[2 ( ) ] cos[2 ( ) ] 2 2 = − − = − − C x V x y A v t A f t 10.2.5 已知波源在原点(x=0)的平面简谐波方程为 y = Acos(bt − cx), A,b,c 均为常量.试求:⑴振幅、频率、波速和波 长;⑵写出在传播方向上距波源 l 处一点的振动方程式,此质点振动 的初相位如何? 解:⑴将 y = Acos(bt − cx) 与标准形式 y = Acos(t − kx) 比 较,ω=b,k=c,∴振幅为 A,频率 v=ω/2π=b/2π,波速 V=ω/k=b/c,波长 λ=V/v=2π/c. ⑵令 x=l, 则 y = Acos(bt − cl) ,此质点振动初相为 – cl. 10.2.6 一平面简谐波逆 x 轴传播,波方程为 = cos 2 ( + + 3), V x y A v t 试利用改变计时起点的方法将波方程化 为最简形式。 解:令 t’=t+3,则 cos 2 ( ' ) V x y = A v t + ,即将计时起点提前 3s, 即可把方程化为如上的最简形式。 10.2.7 平面简谐波方程 5cos2 ( ) 4 x y = t + ,试用两种方法画出 t s 5 3 = 时的波形图(SI)。 解:由波方程可知:A=5, v=4, v=1, λ=v/v=4 t s 5 3 = 时, 5cos2 ( ) 5cos ( ) 5 12 5 4 2 3 y = + = x + x 方法一:令 5 12 x' = x + ,先画出 5cos ' 2 y x = 的波形图,然后将 y 轴右移 5 12 即可。 方法二:找出 x、y 的对应点,根据余弦函数规律描出。 10.2.8 对于平面简谐波 cos2 ( ) x T t S = r − 中,r=0.01m,T=12s, λ=0.30m,画出 x=0.20m 处体元的位移-时间曲线。画出 t=3s,6s 时的 波形图。 解:波方程 cos 2 ( ) 0.01cos 2 ( ) 12 0.3 x t x T t S = r − = − ⑴令 x=0.20, 0.01cos 2 ( ) 0.01cos ( 8) 0.3 6 0.2 12 S = − = t − t ;令 t'=t-8,根据 T=12s 及余弦曲线的规律,先画出 ' 0.01cos ' 6 S t = 的 S’-t’ 曲线,再把 S'轴向左移动 8 秒,即得 S-t 曲线。 S (m) S’ -1 0 1 2 3 4 5 6 7 8 9 10 11 12 t (s) - 0.01 ⑵令 t=3, 0.01cos2 ( ) 0.01cos2 ( ) 12 3 12 0.3 0.3 3 = − = − x x S = x(m) y' y
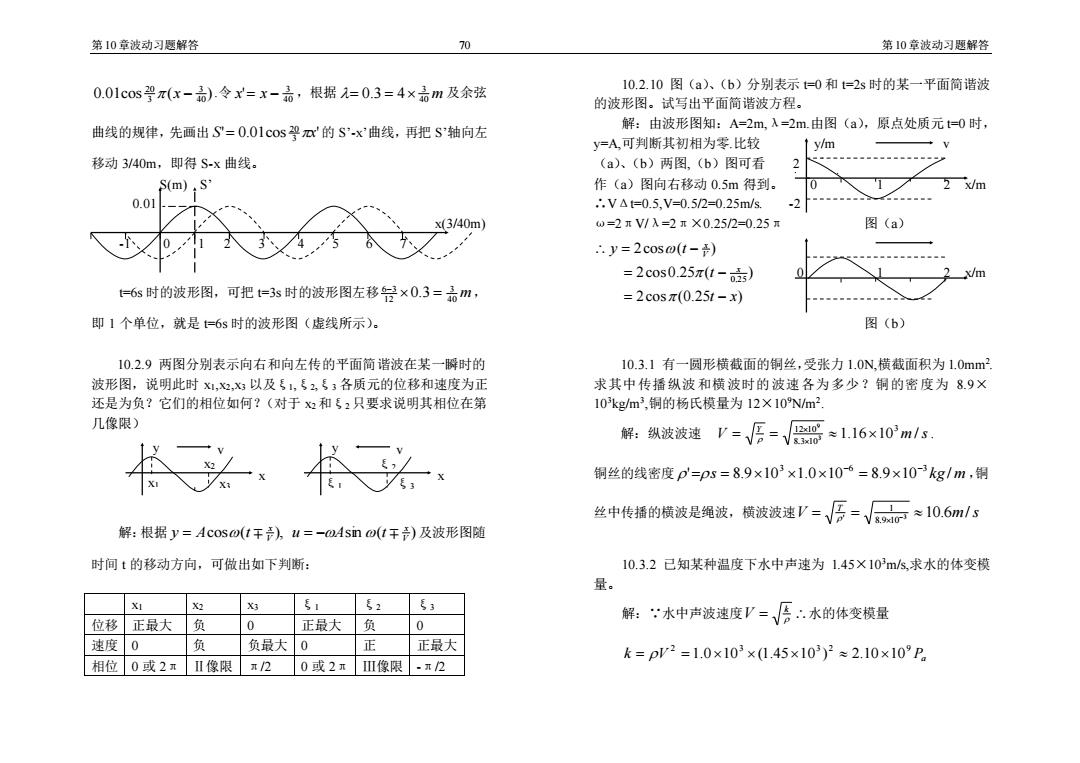
第10章波动习题解答 70 第10章波动习题解答 0.01cos婴π(x-高).令x=x-高,根据=0.3=4×高m及余弦 10.2.10图(a)、(b)分别表示t=0和=2s时的某一平面简谐波 的波形图。试写出平面简谐波方程。 曲线的规律,先画出S=0.01cos9的S'x曲线,再把S轴向左 解:由波形图知:A=2m,入=2m.由图(a),原点处质元=0时, y=A可判断其初相为零比较 y/m V 移动3/40m,即得S-x曲线。 (a)、(b)两图,(b)图可看 S(m).S' 作(a)图向右移动0.5m得到。 2 x/m 0.01 ∴.V△=0.5,V=0.5/2=0.25m/s. x(3/40m) w=2rV/入=2r×0.25/2=0.25F 图(a) ..y=2coso(t-) =2cos0.25π(t-声) x/m =6s时的波形图,可把=3s时的波形图左移号×0.3=品m, =2cosπ(0.25t-x) 即1个单位,就是=6s时的波形图(虚线所示)。 图(b) 10.2.9两图分别表示向右和向左传的平面简谐波在某一瞬时的 10.3.1有一圆形横截面的铜丝,受张力1.0N,横截面积为1.0mm2 波形图,说明此时x1,2,x3以及1,ξ2,3各质元的位移和速度为正 求其中传播纵波和横波时的波速各为多少?铜的密度为89× 还是为负?它们的相位如何?(对于2和2只要求说明其相位在第 103kgm3,铜的杨氏模量为12×10N/m2 几像限) 解:纵波波速V=店=品*1.16×10m/s. 铜丝的线密度p=ps=8.9×103×1.0×10-6=8.9×10-3kg/m,铜 丝中传播的横波是绳波,横波波速V=√后=√odc≈10.6m/s 解:根据y=Acos@(t干),u=-Asno(t干)及波形图随 时间t的移动方向,可做出如下判断: 10.3.2已知某种温度下水中声速为1.45×103m/s,求水的体变模 量。 XI X2 X3 51 52 ξ3 位移正最大 负 0 正最大 负 解::水中声波速度V=√侣水的体变模量 速度0 负 负最大 0 正 正最大 k=pW2=1.0×103×(1.45×103)2≈2.10×10°P. 相位0或2π Ⅱ像限 π/2 0或2π Ⅲ像限 .π2
第10章波动习题解答 70 第10章波动习题解答 0.01cos ( ) 40 3 3 20 x − .令 40 3 x' = x − ,根据 = 0.3 = 4 40 3 m 及余弦 曲线的规律,先画出 ' 0.01cos ' 3 20 S = x 的 S’-x’曲线,再把 S’轴向左 移动 3/40m,即得 S-x 曲线。 S(m) S’ 0.01 x(3/40m) -1 0 1 2 3 4 5 6 7 t=6s 时的波形图,可把 t=3s 时的波形图左移 6 12 −3 0.3 = 40 3 m, 即 1 个单位,就是 t=6s 时的波形图(虚线所示)。 10.2.9 两图分别表示向右和向左传的平面简谐波在某一瞬时的 波形图,说明此时 x1,x2,x3 以及ξ1,ξ2,ξ3 各质元的位移和速度为正 还是为负?它们的相位如何?(对于 x2 和ξ2 只要求说明其相位在第 几像限) 解:根据 cos ( ), sin ( ) V x V x y = A t u = −A t 及波形图随 时间 t 的移动方向,可做出如下判断: x1 x2 x3 ξ1 ξ2 ξ3 位移 正最大 负 0 正最大 负 0 速度 0 负 负最大 0 正 正最大 相位 0 或 2π Ⅱ像限 π/2 0 或 2π Ⅲ像限 -π/2 10.2.10 图(a)、(b)分别表示 t=0 和 t=2s 时的某一平面简谐波 的波形图。试写出平面简谐波方程。 解:由波形图知:A=2m,λ=2m.由图(a),原点处质元 t=0 时, y=A,可判断其初相为零.比较 y/m v (a)、(b)两图,(b)图可看 2 作(a)图向右移动 0.5m 得到。 0 1 2 x/m ∴VΔt=0.5,V=0.5/2=0.25m/s. -2 ω=2πV/λ=2π×0.25/2=0.25π 图(a) 2cos (0.25 ) 2cos 0.25 ( ) 2cos ( ) 0.25 t x t y t x V x = − = − = − 0 1 2 x/m 图(b) 10.3.1 有一圆形横截面的铜丝,受张力 1.0N,横截面积为 1.0mm2 . 求其中传播纵波和横波时的波速各为多少?铜的密度为 8.9× 103kg/m3 ,铜的杨氏模量为 12×109N/m2 . 解:纵波波速 V m s Y 1.16 10 / 3 8.3 10 12 10 3 9 = = . 铜丝的线密度 ' s 8.9 10 1.0 10 8.9 10 k g / m 3 −6 −3 = = = ,铜 丝中传播的横波是绳波,横波波速 V m s T 10.6 / 3 8.9 10 1 ' = = − 10.3.2 已知某种温度下水中声速为 1.45×103m/s,求水的体变模 量。 解:∵水中声波速度 V = k 水的体变模量 V Pa k 2 3 3 2 9 = = 1.010 (1.4510 ) 2.1010 x y x1 x2 x3 v x y ξ1 v ξ2 ξ3

第10章波动习题解答 71 第10章波动习题解答 10.4.1在直径为14cm管中传播的平面简谐波,平均能流密度为 9rgs.cm2,1=300Hz,V=300m/s.(1)求最大能量密度和平均能量密度, 表示:10g台=10g答=10g会+10g (2)求相邻同相位波面间的总能量。 即L1=L2+10g(2)2=20+10g4=20+6.02=26.02dB 解:平均能流密度1=po2A2V=9×103J1sm2 (2)设=3时听不到声音,即对应的声强级L=0 (),能量密度6=p02A2sn2(t-),∴最大能量密度 10g片=10g元-10g2=L2-L3=20-0,.g片=2,÷=102 6m=p02A=头=C=6×105J1m.平均能量密度 124r52=1,4r52,会=(份)2,5=F52=10x10=100m 8=支p0242=8x=3×10J1m3 10.5.1声音千涉仪用于显示声波的干涉,见图。薄膜S在电磁 (2)管的横截面积3=元R2=3.14×(40)2=1.54×102m2, 铁的作用下振动,D为声音检测器,SBD长度可变,SAD长度固定, 声音干涉仪内充满空气。当B处于某一位置时,在D处听到的声强 :相邻同相位波面间的距离为==器=1m,,其间总能量为 为100单位的最小声音,将B移动则声音加大,当B移动1.65cm时 听到强度为900单位的最强音。求:(1)声波的频率:(2)到达D处二 E=e2s=3×10-5×1×1.54×10-2≈4.6×10-7J 声波振幅之比,已知声速为342.4m/s 解:(1)D处听到的声强是由 10.4.3面向街道的窗口面积约40m2,街道上的噪声在窗口的声 SAD和SBD传过来的两列相干波叠 强级为60B,问有多少声功率传入室内?(即单位时间进入多少声 加结果:声强最小,说明两列相干 能) 波在D处的相位相反,合振幅为两 解:据声强级定义:1=10g大=60,g6=6,I=101o, 个分振幅之差:声强最大,说明两 D 列相干波在D处相位相同,合振幅 为两个分振幅之和:两列波在D处的相位差由相反变为相同,相位 所以传入室内的声功率W=IS=106×10-12×40=4.0×10-5W 差改变为π,因此两列波传播距离的改变为入2,有: 10.4.4距一点声源10m的地方,声音的声强级为20dB,求:(1) 距声源5m处的声强级:(2)距声源多远就听不见1000Hz的声音了? =2×1.65×102,1=6.6×102mv=号=0*5188E 解:(1)设r=r1=5m时,声强为1,声强级为IL: =可2=10m时,声强为2,声强级为L2 (2②1,1112=A21A,2,A1A2=√1112=1001900=1/3 1,4m2=124π22,1,=12()2,用声强级
第10章波动习题解答 71 第10章波动习题解答 10.4.1 在直径为 14cm 管中传播的平面简谐波,平均能流密度为 9erg/s.cm2,v=300Hz,V=300m/s.⑴求最大能量密度和平均能量密度, ⑵求相邻同相位波面间的总能量。 解:平均能流密度 2 2 3 2 2 1 I A V 9 10 J /s.m − = = ⑴ ∵能量密度 sin ( ) 2 2 2 V x = A t − ,∴ 最大能量密度 5 3 300 2 2 2 2 9 10 max 6 10 / 3 A V I J m − = = = = − . 平均能量密度 5 3 2 max 2 2 1 2 1 A 3 10 J / m − = = = ⑵管的横截面积 2 2 2 2 2 14 10 3.14 ( ) 1.54 10 2 s R m − = = = − , ∵相邻同相位波面间的距离为 = V v = 300 300 =1m ,∴其间总能量为 E s J 5 2 7 3 10 1 1.54 10 4.6 10 − − − = = 10.4.3 面向街道的窗口面积约 40m2 ,街道上的噪声在窗口的声 强级为 60dB,问有多少声功率传入室内?(即单位时间进入多少声 能) 解:据声强级定义: 0 6 10lg 60, lg 6, 10 0 0 Il I I I I I I = = = = , 所以传入室内的声功率 W IS W 6 12 5 10 10 40 4.0 10 − − = = = 10.4.4 距一点声源 10m 的地方,声音的声强级为 20dB,求:⑴ 距声源 5m 处的声强级;⑵距声源多远就听不见 1000Hz 的声音了? 解:⑴设 r=r1=5m 时,声强为 I1,声强级为 IL1; r=r2=10m 时,声强为 I2,声强级为 IL2 2 1 2 2 2 2 2 1 1 4 4 , ( ) 1 2 r r I r = I r I = I ,用声强级 表示: 2 10lg 10lg 10lg 10lg( ) 1 2 0 2 2 0 1 2 2 2 0 1 r r I I I r I r I I = = + 即 IL IL r dB r 10lg( ) 20 10lg 4 20 6.02 26.02 2 1 2 1 2 = + = + = + = ⑵设 r=r3 时听不到声音,即对应的声强级 IL3=0 2 10lg 10lg 10lg 2 3 20 0, lg 2, 10 3 2 3 2 0 3 0 2 3 2 = − = − = − = = I I I I I I I I I I IL IL I r I r r I r m I r r I I 4 4 , ( ) , 3 2 10 10 100 2 2 3 3 2 2 2 3 2 3 2 2 3 = = = = = 10.5.1 声音干涉仪用于显示声波的干涉,见图。薄膜 S 在电磁 铁的作用下振动,D 为声音检测器,SBD 长度可变,SAD 长度固定, 声音干涉仪内充满空气。当 B 处于某一位置时,在 D 处听到的声强 为 100 单位的最小声音,将 B 移动则声音加大,当 B 移动 1.65cm 时 听到强度为 900 单位的最强音。求:⑴声波的频率;⑵到达 D 处二 声波振幅之比,已知声速为 342.4m/s 解:⑴D 处听到的声强是由 SAD和SBD传过来的两列相干波叠 加结果;声强最小,说明两列相干 波在 D 处的相位相反,合振幅为两 个分振幅之差;声强最大,说明两 列相干波在 D 处相位相同,合振幅 为两个分振幅之和;两列波在 D 处的相位差由相反变为相同,相位 差改变为π,因此两列波传播距离的改变为λ/2,有: m v Hz V 2 1.65 10 , 6.6 10 , 2 5188 6.6 10 2 2 342.4 2 = = = = − − − ⑵ / / , 1 / 2 1 / 2 100/900 1/3 2 2 2 I 1 I 2 = A1 A A A = I I = = r B A S D

第10章波动习题解答 72 第10章波动习题解答 10.52两个波源发出横波,振动方向与纸面垂直,两波源具有 方向与入射波传播方向相反:入射波在原点处振动初相为零,设反 相同的相位,波长0.34m.(1)至少求出三个x数值使得在P点合振动 射波在坐标原点处振动初相为中,固定端反射有半波损失,所以 最强,(2)求出三个x数值使得在P点的合振动最弱。 解:由于两个波源的相位相同, 0-中=癸2π+π,中=-(赞+1)π=-(捌品+)π=-61π.综合 因而二波在P点引起的两个分振动的 E--! 以上考虑,反射波方程为y=10×10-cos2000π(t+卖)-61π] 相位差△=-2π=2π是 x 山 =10×10-4cos2000π(t+哥)-π] (1)当2π=2nπ(n=0,1,2…)时, 合振动最强。取n=0,1,2,得x1-0,X2=入=0.34m,x3=2入=0.68m 10.5.5入射波方程为y=Acos2π(号+),在x=0处的自由端 (2)当2π产=(2n+1)π(n=0,1,2…)时,合振动最弱.取n=0,1,2 反射,求反射波的波方程。无振幅损失。 得x1=入/2=0.17m,x2=3入/2=0.51m,x3=5入/2=0.85m 解:反射波的振幅、周期、波长与入射波相同:反射波传播方 向与入射波相反:由于在x=0处的自由端反射,无半波损失,反射 10.5.3试证明两列频率相同,振动方向相同、传播方向相反而 波与入射波在原点的初相相同。综合以上考虑,反射波方程为 振幅大小不同的平面简谐波相叠加可形成一驻波与一行波的叠加。 y=Acos2π(号-) 证明:设满足要求的两列平面简谐波的波方程为: 乃=A1cos(o1-kx),月2=A2cos(@t+kx,A1>A y=A cos(@t-kx)+A,cost@t+kx) 10.5.610.5.7图表示某一瞬时入射波的波形图,分别画出在固 =(A-A +A2)cos(@t-kx)+A cos(@t+kx) 定端反射和在自由端反射时,反射波的波形图,无振幅损失。 =(A-A)cos(@1-kx)+A,[cos(@t+kx)+cos(@t-kx)] 解: =(A-A2 )cos(@t-kx)+24,cos kxcosot (应用三角函数公式:cosa+cosB=2cos生cos“) 显然,前一项表示一行波,后一项为一驻波 方法:可先把界面后边的入射波补画上去,如图1:固定端反射 时,损失半个波长,可把界面后边的波形去掉半个波长,然后把剩 10.5.4入射波y=10×10一cos2000m(t-孟】在固定端反射, 余波形映射过去即可,如图2:自由端反射,无半波损失,直接把界 坐标原点与固定端相距0.51m,写出反射波方程.无振幅损失.(SI) 面后边的波形映射过去即可,如图3。 解:反射波的振幅、频率、波速均与入射波相同:反射波传播
第10章波动习题解答 72 第10章波动习题解答 10.5.2 两个波源发出横波,振动方向与纸面垂直,两波源具有 相同的相位,波长 0.34m.⑴至少求出三个 x 数值使得在 P 点合振动 最强,⑵求出三个 x 数值使得在 P 点的合振动最弱。 解:由于两个波源的相位相同, 因而二波在 P 点引起的两个分振动的 l P 相位差 l l x x 2 2 ( ) = = − − l-x ⑴当 2 = 2n (n = 0,1,2 x …)时, 合振动最强。取 n=0,1,2, 得 x1=0, x2=λ=0.34m, x3=2λ=0.68m ⑵当 2 = (2n +1) (n = 0,1,2 x …)时,合振动最弱。取 n=0,1,2, 得 x1=λ/2=0.17m, x2=3λ/2=0.51m, x3=5λ/2=0.85m 10.5.3 试证明两列频率相同,振动方向相同、传播方向相反而 振幅大小不同的平面简谐波相叠加可形成一驻波与一行波的叠加。 证明;设满足要求的两列平面简谐波的波方程为: A A t k x A k x t A A t k x A t k x t k x A A A t k x A t k x y A t k x A t k x y A t k x y A t k x A A ( ) cos( ) 2 cos cos ( ) cos( ) [cos( ) cos( )] ( ) cos( ) cos( ) cos( ) cos( ) cos( ), cos( ), 1 2 2 1 2 2 1 2 2 2 1 2 1 1 2 2 1 2 = − − + = − − + + + − = − + − + + = − + + = − = + (应用三角函数公式: 2 2 cos cos 2cos cos + − + = ) 显然,前一项表示一行波,后一项为一驻波 10.5.4 入射波 10 10 cos[2000 ( )] 34 4 x y = t − − 在固定端反射, 坐标原点与固定端相距 0.51m,写出反射波方程.无振幅损失.(SI) 解:反射波的振幅、频率、波速均与入射波相同;反射波传播 方向与入射波传播方向相反;入射波在原点处振动初相为零,设反 射波在坐标原点处振动初相为φ,固定端反射有半波损失,所以 0 2 , ( 1) ( 1) 61 34/1000 2 4 4 0.51 − = + = − + = − + = − .综合 以上考虑,反射波方程为 10 10 cos[2000 ( ) 61 ] 34 4 = + − − x y t 10 10 cos[2000 ( ) ] 34 4 = + − − x t 10.5.5 入射波方程为 cos2 ( ) x T t y = A + ,在 x=0 处的自由端 反射,求反射波的波方程。无振幅损失。 解:反射波的振幅、周期、波长与入射波相同;反射波传播方 向与入射波相反;由于在 x=0 处的自由端反射,无半波损失,反射 波与入射波在原点的初相相同。综合以上考虑,反射波方程为 cos2 ( ) x T t y = A − 10.5.6 10.5.7 图表示某一瞬时入射波的波形图,分别画出在固 定端反射和在自由端反射时,反射波的波形图,无振幅损失。 解: 方法:可先把界面后边的入射波补画上去,如图 1;固定端反射 时,损失半个波长,可把界面后边的波形去掉半个波长,然后把剩 余波形映射过去即可,如图 2;自由端反射,无半波损失,直接把界 面后边的波形映射过去即可,如图 3。 x 1 2 3