(2)准均匀的B样条曲线 与均匀B样条曲线的差别在于两端节点 具有重复度飞,这样的节点矢量定义了 准均匀的B样条基。 图6.5.2准均匀三次B样条曲线 教学建模
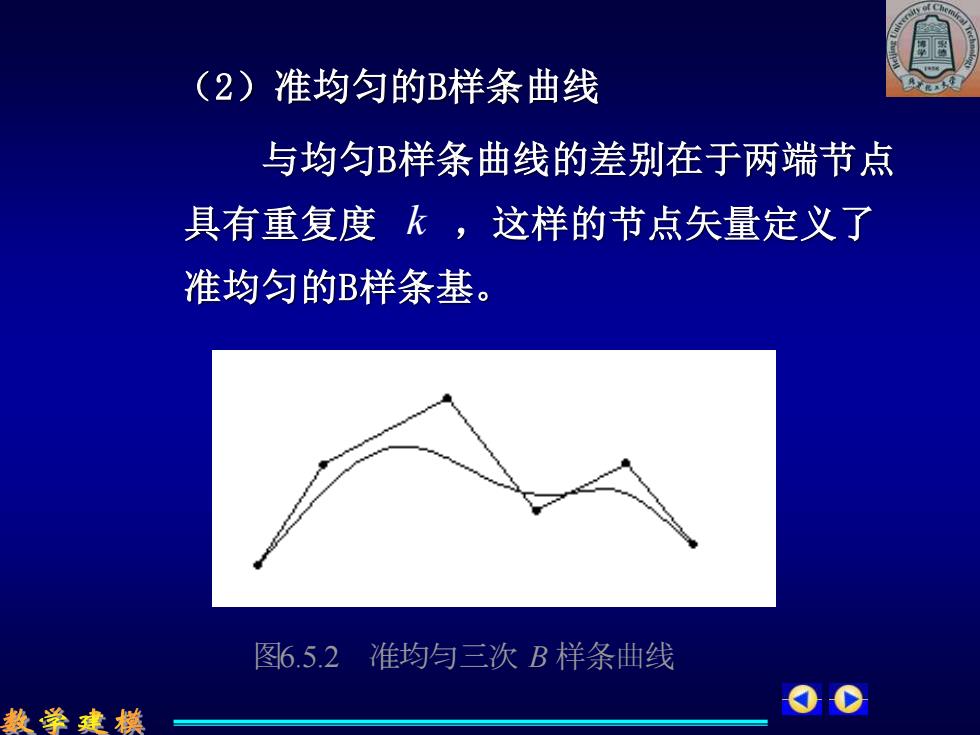
(2)准均匀的B样条曲线 与均匀B样条曲线的差别在于两端节点 具有重复度 ,这样的节点矢量定义了 准均匀的B样条基。 图6.5.2 准均匀三次 B 样条曲线 k
(3)分段Bezierl曲线 节点矢量中两端节点具有重复度飞,所有 内节点重复度为飞-1,这样的节点矢量定义了 分段的Bernstein:基 图6.5.3三次分段Bezier曲线 款学建模
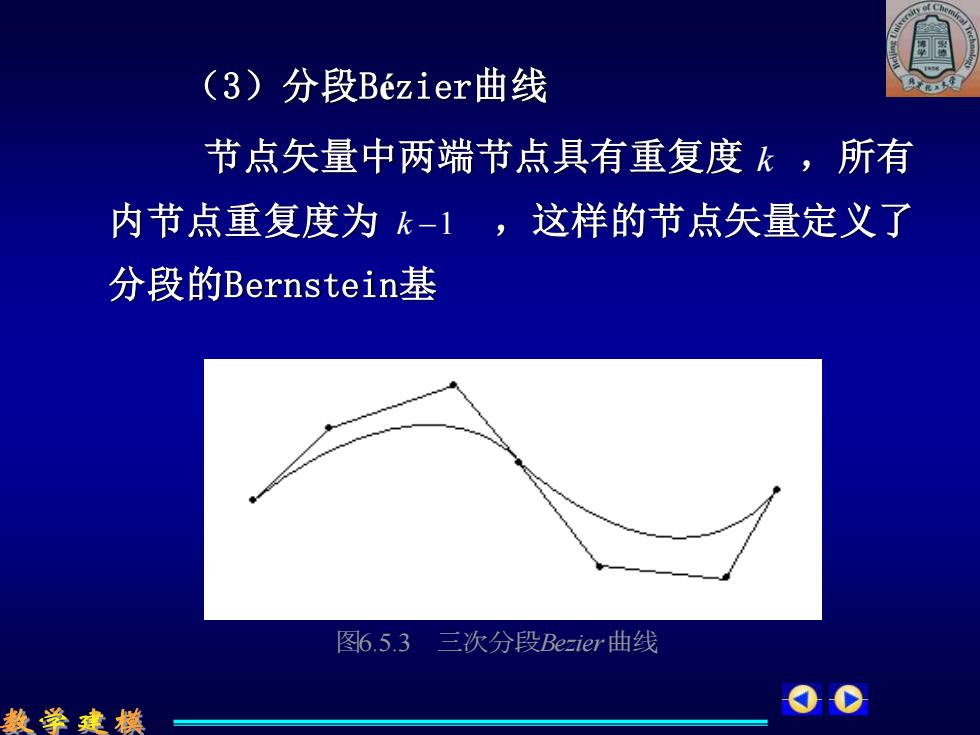
(3)分段Bézier曲线 节点矢量中两端节点具有重复度 ,所有 内节点重复度为 ,这样的节点矢量定义了 分段的Bernstein基 图6.5.3 三次分段Bezier曲线 k −1 k

三.B样条曲线的性质 1.局部性 k阶B样条曲线上参数为t∈[,l]的一点P) 至多与k个控制顶点P=i-k+1,,)有关 2.连续性 Pt)在重节点t,(k≤i≤n),处的连续阶不低于 k-1-r。 整条曲线的连续阶不低于k-1-了m 其中r表示位于区间G,t)内的节点的最 大重数。 数学建模
三. B样条曲线的性质 k −1−r 1.局部性 阶B样条曲线上参数为 1 , i i+ t t t 的一点 P(t) 至多与 个控制顶点 P (j i k i) j = − +1, , 有关 2. 连续性 P(t) 在 重节点 t (k i n) i ,处的连续阶不低于 。整条曲线的连续阶不低于 1 max k − − r 其中 max r 表示位于区间 ( ) 1 1 , k− n+ t t 内的节点的最 大重数。 k k r

3.凸包性 Pt)在区间(G,t),k-1≤i≤n上的部分位于k 个点Pk1,…,P的凸包C,内,整条曲线则位于 各凸包C,的并集Uc,之内。 i=k-1 4.分段参数多项式 P(在每一区间亿,),k-1≤i≤n上都是次数 不高于k-1的参数t的多项式(是参数t 的k一1次分段多项式。 数学建模
3.凸包性 P(t) 在区间 (t i ,t i+1 ),k −1 i n 上的部分位于 个点 Pi k Pi , , − +1 的凸包 Ci 内,整条曲线则位于 各凸包 Ci 的并集 n i k Ci = −1 之内。 4.分段参数多项式 P(t) 在每一区间 (t i ,t i+1 ),k −1 i n 上都是次数 不高于 的参数 的多项式, P(t 是参数 ) 的 次分段多项式。 k k −1 k −1 t t