电子科技大学：《信号处理理论与算法》课程教学资源（课件讲稿）第一部分 CH06 FIR滤波器设计

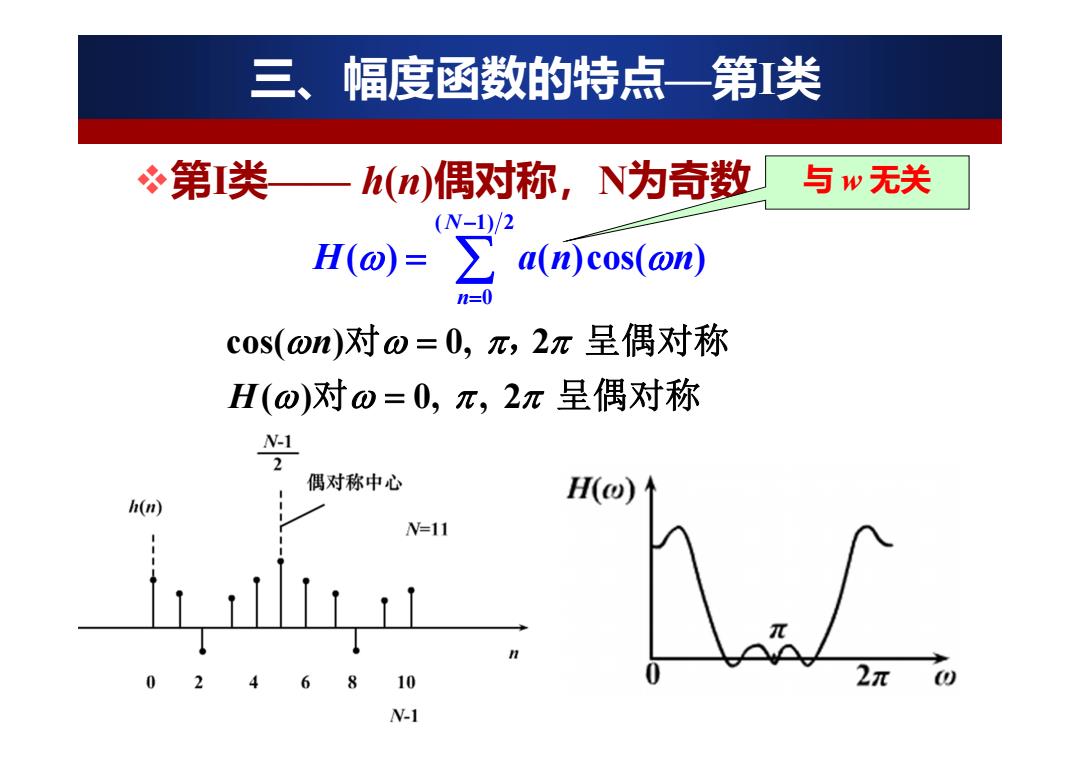
三、幅度函数的特点一第类 必第类 h(m偶对称，N为奇数 与w无关 (N-1)/2 H(o)=∑a((n)cos(om) n=0 c0s(0n)对o=0,π，2π呈偶对称 H(o)对0=0，π，2π呈偶对称 2 偶对称中心 H() h(m) N=11 10 2π o N-1

H( ) 0, , 2  对 呈偶对称    cos( ) 0, 2 n 对   ， 呈偶对称 三、幅度函数的特点—第I类 第I类—— h(n)偶对称，N为奇数 ( 1) 2 0 ( ) ( )cos( ) N n H an n       与 w 无关

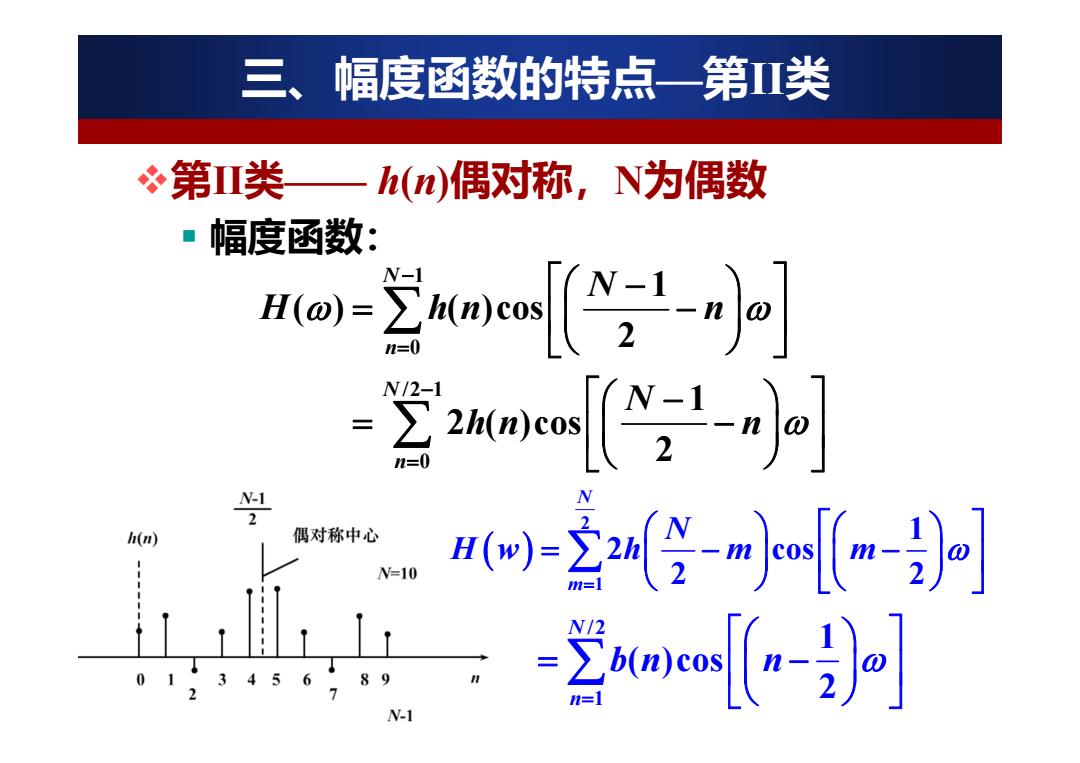
三、幅度函数的特点一第Ⅱ类 冬第类 h(n)偶对称，N为偶数 幅度函数： io-2oor[〔：'p] 1=0 2ane-[1-小 1 2 h(n) 偶对称中心 WN-10 -空4mjr[m] m= 45 6 -这owr W-1

1 0 /2 1 0 1 ( ) ( )cos 2 1 2 ( )cos 2 N n N n N H hn n N hn n                                   幅度函数： 三、幅度函数的特点—第II类 第II类—— h(n)偶对称，N为偶数 /2 1 1 ( )cos 2 Nn bn n                 2 1 1 2 cos 2 2 N m N Hw h m m                    

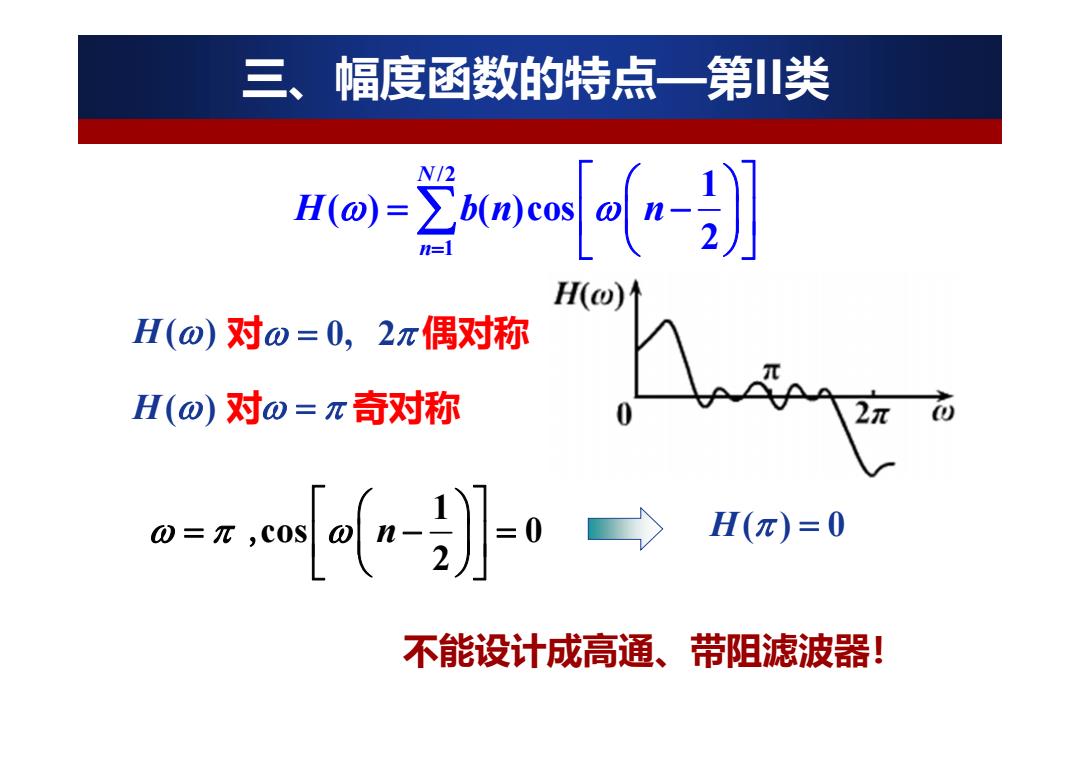
三、幅度函数的特点一第川类 no-豆xacn-】 N2 H(⊙)1 H(o)对o=0,2π偶对称 H(o)对o=π奇对称 0=,awa-】-0→ H(π)=0 不能设计成高通、带阻滤波器！

H() 0   1 cos 0 2    n                , 不能设计成高通、带阻滤波器！ /2 1 1 ( ) ( )cos 2 Nn H bn n                三、幅度函数的特点—第II类 H( )  对 偶对称   0, 2  H( )  对 奇对称   

三、幅度函数的特点一第类 冬第类一 h(n)奇对称，N为奇数 相蜜数：o)-立4msn[小] N-1 n=0 [ -N-I 奇对称 h(D奇对称，N为奇数 N- 0 2 o-空叫'nnn-玄nmam N-1 N-1 =1

-1 -1 sin - 2 2 N N n              关于 奇对称 1 0 1 ( ) ( )sin 2 Nn N H hn n                 三、幅度函数的特点—第III类 幅度函数： 1 1 2 1 2 1 1 2 sin( ) 2 ( ) ( )sin( ) n N N m N H  h mm cn n                 hn N ( )奇对称， 为奇数 第III类—— h(n)奇对称，N为奇数 1 0 2 N h       