电子科技大学：《信号处理理论与算法》课程教学资源（课件讲稿）第一部分 CH06 FIR滤波器设计

线性相位条件 第一类线性相位：0(o)=-o W-1 H(eo)=∑n)eom=±H(eo)leor t=0 ±Helo(or）-2(jos(on）sinor时_2aojs小n(am） n=( n=0 ±H(e)小sin(or)=∑(n)sin(on) cos(@r） ∑h(n)cos(on) n( ∑h(n)sin(or)cos(on)-∑(n）cos(@r)小sin(om）=0 如何满足？ ∑(n）sin[(x-n)o]=0r

     1 0 ( ) cos cos N j n He hn n              1 0 ( ) sin sin N j n He hn n                   1 0 1 0 sin sin cos cos N n N n hn n hn n                       1 1 0 0 sin cos cos sin 0 N N n n hn n hn n               1 0 sin 0 N n hn n            一、线性相位条件 第一类线性相位： 1 0 ( ) () ( ) N j j n j j n H e hne He e            如何满足？  ( )    

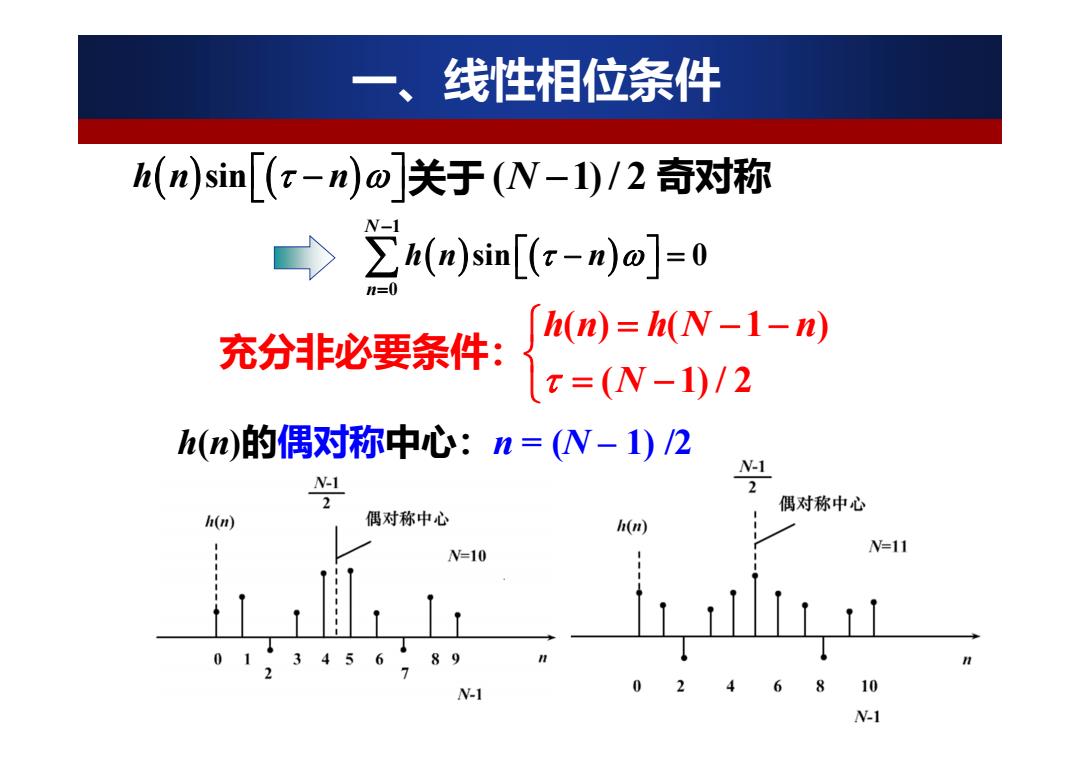
线性相位条件 h(n)sim[(x-n)o关于(N-l)/2奇对称 ∑h(n)sin[(x-n)）o]=0 h(m)=h(N-1-n) 充分非必要条件： x=(N-1)/2 h(n)的偶对称中心：n=(N-1)/2 N-1 2 偶对称中心 h(n) 偶对称中心 h(n) N=10 W=11 456 89 10 N-1

h(n)的偶对称中心：n = (N – 1) /2 一、线性相位条件 充分非必要条件： () ( 1 ) ( 1) / 2 hn hN n  N          1 0 sin 0 N n hn n            hn n    sin       关于 ( 1) / 2 N  奇对称

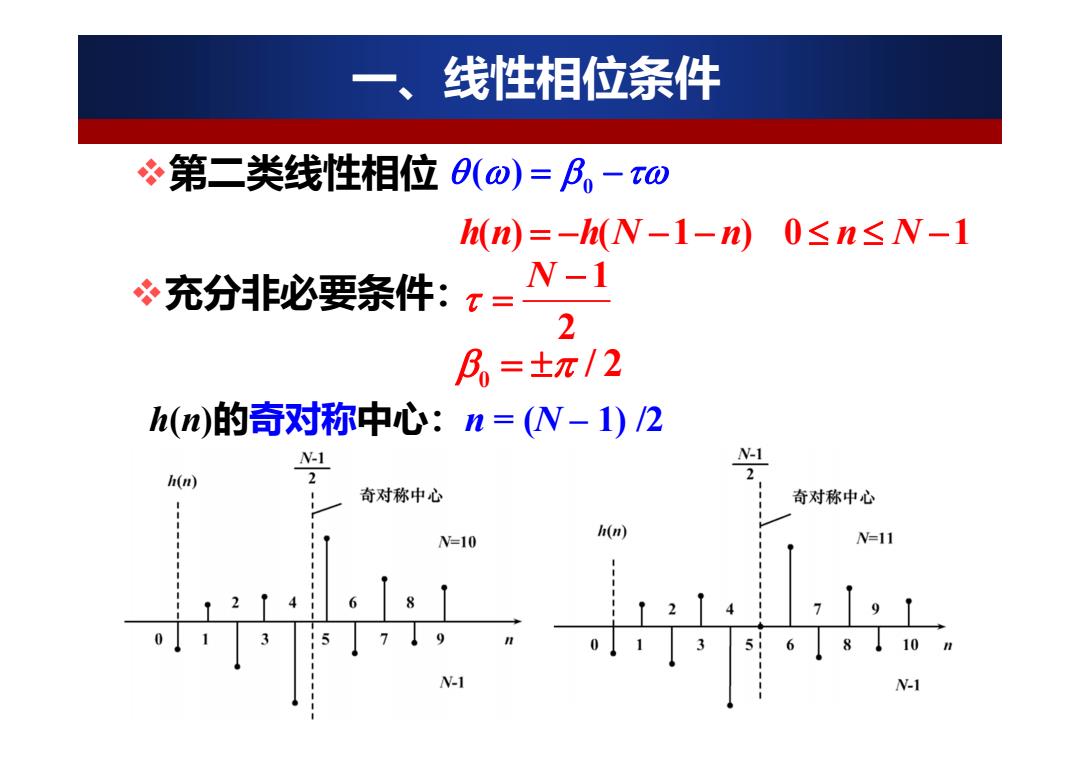
线性相位条件 第二类线性相位(o)=阝，-xo (n)=-(N-1-n0≤n≤N-1 充分非必要条件：x= N-1 2 =±π/2 h(n)的奇对称中心：n=(N-1)/2 N-1 N-1 h(n) 奇对称中心 奇对称中心 h(n =10 N=11 V-

第二类线性相位 0  ( )      hn hN n n N () ( 1 ) 0 1       1 2 N    0    / 2 h(n)的奇对称中心：n = (N – 1) /2 一、线性相位条件 充分非必要条件：

二、线性相位FIR滤波器频率响应的特点 分析频率响应，确定不同条件下滤波器的适用范围 h(n)=±h(N-1-n)0≤n≤N-1 He=∑dmg”=∑±uN-1-mz N- =0 =0 令m=N-1-n N-I H(z)=∑±h(m)zw-1m m=0 N-I =士z-w-∑mz" m=0 =±zN-DH(z1)

二、线性相位FIR滤波器频率响应的特点 1 1 0 0 () () ( 1 ) N N n n n n H z hnz hN nz               1 (1) 0 ( ) N N m m H z hmz        ( 1) 1 ( ) N z H z      令mN n   1 hn hN n n N () ( 1 ) 0 1       1 ( 1) 0 ( ) N N m m z hmz        分析频率响应，确定不同条件下滤波器的适用范围

二、线性相位FR滤波器频率响应的特点 H(z)=±zN-DH(z) Ha)=[He)士&wHe] 2 wg±a2Aae W-1 =2[e±n] 1s0 N-1N-1 =2】 n=0 2

1 ( 1) 1 () () ( ) 2 N Hz Hz z Hz         1 1 ( 1) 0 0 1 () () 2 N N nN n n n hnz z hnz                 1 ( 1) 0 1 ( ) 2 N n Nn n hn z z z            1 1 1 1 2 2 2 0 ( ) 2 N N n n N N n z z z hn                                 ( 1) 1 ( ) N H z z Hz      二、线性相位FIR滤波器频率响应的特点