
正弦承数图象的对称性 北京市第十九中学檀晋轩 【教学目标】 1,使学生掌握正弦函数图象的对称性及其代数表示形式,理解诱导公式 血(不-)=如x(x∈R)与血(2不-为=-血X《x∈R)的几何意义,体会正弦函 数的对称性 2。在探究过程中渗透由具体到抽象,由特殊到一般以及数形结合的思想方法,提高 学生观察、分析、抽象概括的能力 3.通过具体的探究活动,培养学生主动利用信息技术研究并解决数学问题的能力, 增强学生之间合作与交流的意识 【教学重点】 正弦函数图象的对称性及其代数表示形式, 【教学难点】 用等式表示正弦函数图象关于直线“2对称和关于点(π,0对称 【教学方法】 教师启发引导与学生自主探究相结合。 【教学手段】 计算机、图形计算器(学生人手一台)。 【教学过程】 一、复习引入 1.展示生活实例 对称在自然界中有者丰富多彩的显现,各种对称图案、对称符号也都十分普遍(见 下图
正弦函数图象的对称性 北京市第十九中学 檀晋轩 【教学目标】 1. 使 学生 掌握 正 弦函 数 图象 的对 称 性及 其 代数 表示 形 式, 理 解诱 导 公 式 ( R)与 ( R)的几何意义,体会正弦函 数的对称性. 2.在探究过程中渗透由具体到抽象,由特殊到一般以及数形结合的思想方法,提高 学生观察、分析、抽象概括的能力. 3.通过具体的探究活动,培养学生主动利用信息技术研究并解决数学问题的能力, 增强学生之间合作与交流的意识. 【教学重点】 正弦函数图象的对称性及其代数表示形式. 【教学难点】 用等式表示正弦函数图象关于直线 对称和关于点 对称. 【教学方法】 教师启发引导与学生自主探究相结合. 【教学手段】 计算机、图形计算器(学生人手一台). 【教学过程】 一、复习引入 1.展示生活实例 对称在自然界中有着丰富多彩的显现,各种对称图案、对称符号也都十分普遍(见 下图)

5 000 2.复习对称概念 初中我们已经学习过轴对称图形和中心对称图形的有关概念: 轴对称图形一一将图形沿一条直线折叠,直线两侧的部分能够互相重合: 中心对称图形一一将图形绕一个点旋转180°,所得图形与原图形重合 3.作图观察 请同学们用图形计算器画出正弦函数的图象(见图),仔细观察正弦曲线是否是对 称图形?是轴对称图形还是中心对称图形? 西 AA
2.复习对称概念 初中我们已经学习过轴对称图形和中心对称图形的有关概念: 轴对称图形——将图形沿一条直线折叠,直线两侧的部分能够互相重合; 中心对称图形——将图形绕一个点旋转 180°,所得图形与原图形重合. 3.作图观察 请同学们用图形计算器画出正弦函数的图象(见图),仔细观察正弦曲线是否是对 称图形?是轴对称图形还是中心对称图形?

4.猜想图形性质 经过简单交流后,能够发现正弦曲线既是轴对称图形也是中心对称图形,并能够猜 想出一部分对称轴和对称中心.(教师点评并板书) 如何检验猜想是否正确? 我们知道,诱号公式m(一利=一加本(不R),刻画了正弦曲线关于原点对称, 而Cos(一x)=c03x(x∈R),刻画了余弦曲线关于y轴对称从这两个特殊的例子中 我们得到一些启发,如果我们能够用代数式表示所发现的对称性,就可以从代数上进行 严格证明, 今天我们利用图形计算器来研究正弦函数图象的对称性.(板书课题) 二、探究新知 分为两个阶段,第一阶段师生共同探讨正弦曲线的轴对称性质,第二阶段学生自主 探索正弦曲线的中心对称性质 (一)对于正弦曲线轴对称性的研究 第一阶受,实例分析一一对正弦曲线关于直线2对称的研究。一 1.直观探索一一利用图形计算器的绘图功能进行探素 园学在用串标系中出正这电我和真产2的相兔,选的当度如光衣分菊 用画图功能对问题进行探索研究(见图),在直线“2两侧正弦函数值有什么变化规律? 给学生一定的时间操作、观察、归纳、交流,最后得出猜想:当自李是X《 2左右 对称取值时,正弦函数值相等
4.猜想图形性质 经过简单交流后,能够发现正弦曲线既是轴对称图形也是中心对称图形,并能够猜 想出一部分对称轴和对称中心.(教师点评并板书) 如何检验猜想是否正确? 我们知道, 诱导公式 ( R),刻画了正弦曲线关于原点对称, 而 ( R),刻画了余弦曲线关于 轴对称. 从这两个特殊的例子中 我们得到一些启发,如果我们能够用代数式表示所发现的对称性,就可以从代数上进行 严格证明. 今天我们利用图形计算器来研究正弦函数图象的对称性.(板书课题) 二、探究新知 分为两个阶段,第一阶段师生共同探讨正弦曲线的轴对称性质,第二阶段学生自主 探索正弦曲线的中心对称性质. (一)对于正弦曲线轴对称性的研究 第一阶段,实例分析——对正弦曲线关于直线 对称的研究. 1.直观探索——利用图形计算器的绘图功能进行探索 请同学们在同一坐标系中画出正弦曲线和直线 的图象,选择恰当窗口并充分利 用画图功能对问题进行探索研究(见图),在直线 两侧正弦函数值有什么变化规律? 给学生一定的时间操作、观察、归纳、交流,最后得出猜想:当自变量在 左右 对称取值时,正弦函数值相等
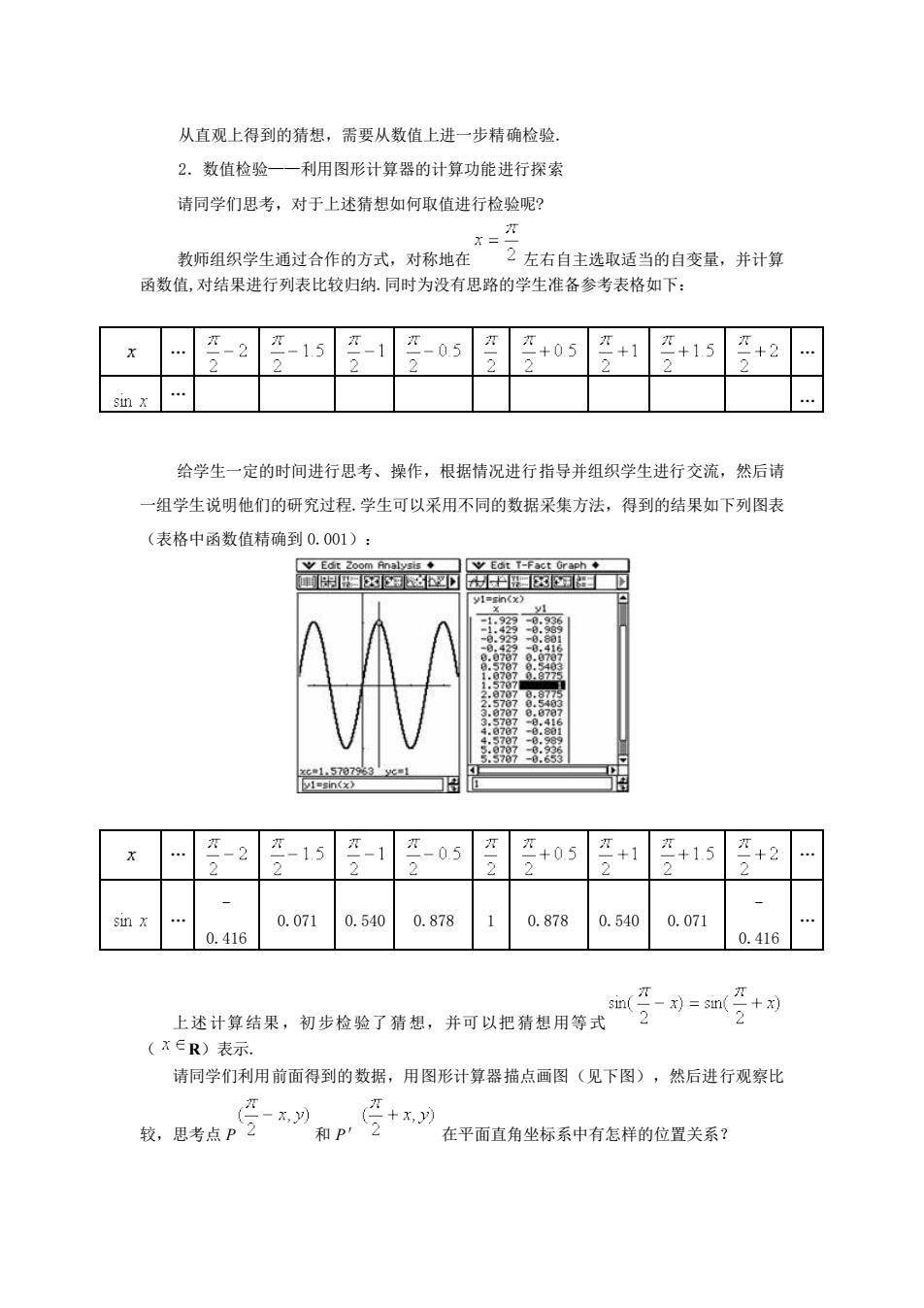
从直观上得到的猜想,需要从数值上进一步精确检验。 2。数值检验一一利用图形计算器的计算功能进行探索 请同学们思考,对于上述猜想如何取值进行检验呢 抗相织学生活数合作的方式,对将格在”一左右自主速适的自支,并计获 函数值,对结果进行列表比较归纳.同时为没有思路的学生准备参考表格如下: x -2交-15-1-05+05+1+15+2 给学生一定的时间进行思考、操作,根据情况进行指导并组织学生进行交流,然后请 组学生说明他们的研究过程.学生可以采用不同的数据采集方法,得到的结果如下列图表 (表格中函数值精确到0.001): -2-15 -1-05+05+1 +15+2 0.071 0.5400.87810.8780.5400.071 0.416 0.416 吉并结果,初步检险了菊起,并可以起骑想用等式(受功=如孕+可 2 (x∈R)表示. 请同学们利用前面得到的数据,用图形计算器描点画图(见下图),然后进行观察比 -x 较,思考点P2 在平面直角坐标系中有怎样的位置关系?
从直观上得到的猜想,需要从数值上进一步精确检验. 2.数值检验——利用图形计算器的计算功能进行探索 请同学们思考,对于上述猜想如何取值进行检验呢? 教师组织学生通过合作的方式,对称地在 左右自主选取适当的自变量,并计算 函数值,对结果进行列表比较归纳.同时为没有思路的学生准备参考表格如下: . . . . 给学生一定的时间进行思考、操作,根据情况进行指导并组织学生进行交流,然后请 一组学生说明他们的研究过程.学生可以采用不同的数据采集方法,得到的结果如下列图表 (表格中函数值精确到 0.001): . . . - 0.416 0.071 0.540 0.878 1 0.878 0.540 0.071 - 0.416 . 上述计算结果,初步检验了猜想,并可以把猜想用等式 ( R)表示. 请同学们利用前面得到的数据,用图形计算器描点画图(见下图),然后进行观察比 较,思考点 P 和 P′ 在平面直角坐标系中有怎样的位置关系?
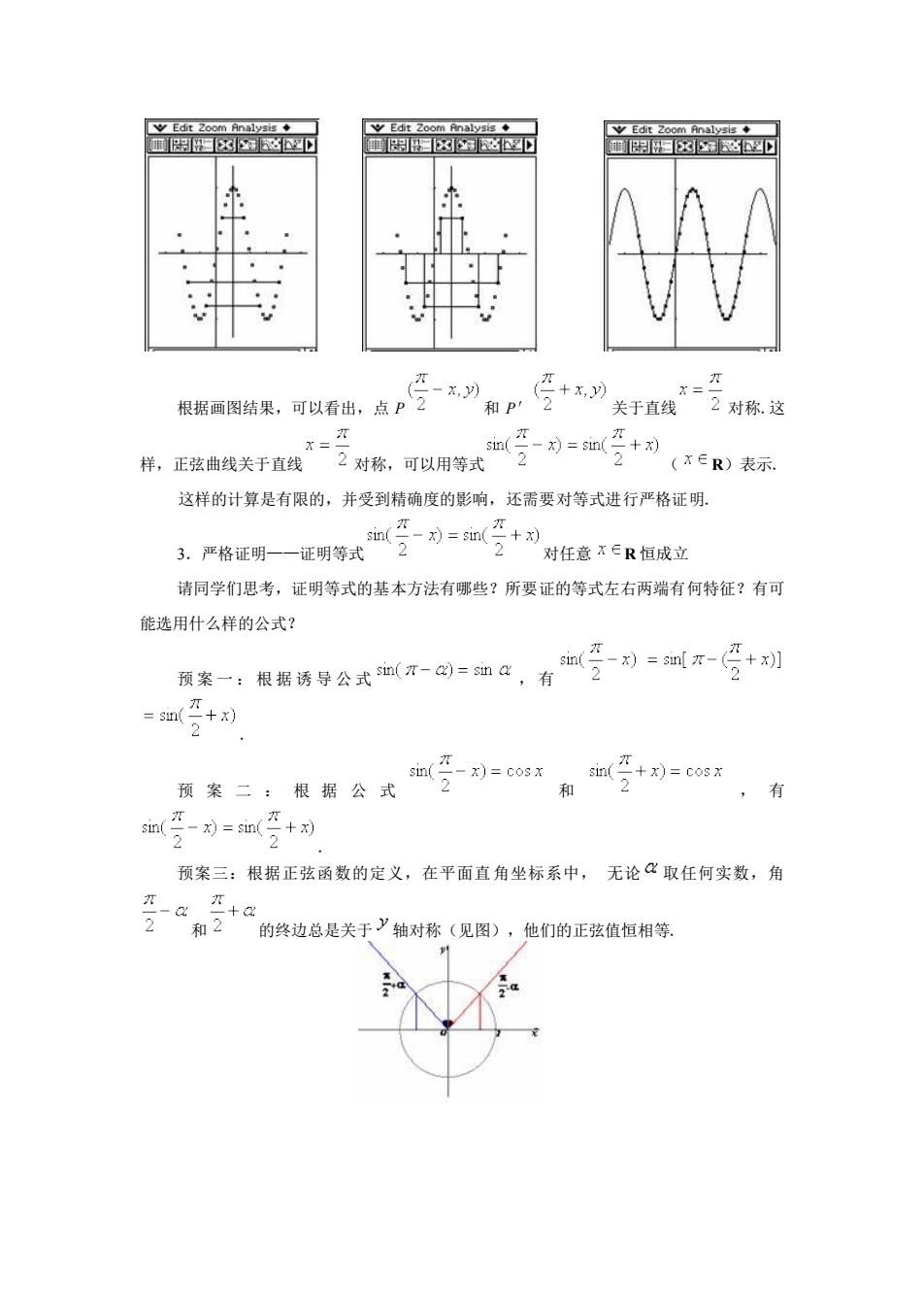
yEt2oAn◆ wEdt2 oom Bnalysis◆ 图x6多Y 图☒离D 关于直艺对称这 这样的计算是有限的,并受到精确度的影响,还需要对等式进行严格证明。 对任意x∈R恒成立 请同学们思考,证明等式的基本方法有哪些?所要证的等式左右两端有何特征?有可 能选用什么样的公式? 要:限帮涛学公式-回如6,有如空司到-召别 双案二,根聚会式如(写列=cx m(+)=co8x 和 ,有 预案三:根据正弦函数的定义,在平面直角坐标系中,无论取任何实数,角 的终边总是关于》轴对称(见图),他们的正弦值恒相等
根据画图结果,可以看出,点 P 和 P′ 关于直线 对称.这 样,正弦曲线关于直线 对称,可以用等式 ( R)表示. 这样的计算是有限的,并受到精确度的影响,还需要对等式进行严格证明. 3.严格证明——证明等式 对任意 R 恒成立 请同学们思考,证明等式的基本方法有哪些?所要证的等式左右两端有何特征?有可 能选用什么样的公式? 预案一:根据诱导公式 , 有 . 预 案 二 : 根 据 公 式 和 , 有 . 预案三:根据正弦函数的定义,在平面直角坐标系中, 无论 取任何实数,角 和 的终边总是关于 轴对称(见图),他们的正弦值恒相等