
“平面向量数量积的物理背景及其含义”说课稿 宁夏银川唐徕回民中学马海军 说课内容:普通高中课程标准实验教科书(人教A版)《数学必修4》第 二章第四节“平面向量的数量积”的第一课时-一平面向量数量积的物理背景及 其含义 下面,我从背景分析、教学目标设计、课堂结构设计、教学过程设计、教 学媒体设计及教学评价设计六个方面对本节课的思考进行说明。 一、背景分析 1、学习任务分析 平面向量的数量积是继向量的线性运算之后的又一重要运算,也是高中数 学的一个重要概念,在数学、物理等学科中应用十分广泛。本节内容教材共安 排两课时,其中第一课时主要研究数量积的概念,第二课时主要研究数量积的 坐标运算,本节课是第一课时。 本节课的主要学习任务是通过物理中“功”的事例抽象出平面向量数量积 的概念,在此基础上探究数量积的性质与运算律,使学生体会类比的思想方法, 进一步培养学生的抽象概括和推理论证的能力。其中数量积的概念既是对物理 背景的抽象,又是研究性质和运算律的基础。同时也因为在这个概念中,既有 长度又有角度,既有形又有数,是代数、几何与三角的最佳结合点,不仅应用 广泛,而且很好的体现了数形结合的数学思想,使得数量积的概念成为本节课 的核心概念,自然也是本节课教学的重点。 2、学生情况分析 学生在学习本节内容之前,己熟知了实数的运算体系,掌握了向量的概念 及其线性运算,具备了功等物理知识,并且初步体会了研究向量运算的一般方 法:即先由特殊模型(主要是物理模型)抽象出概念,然后再从概念出发,在 与实数运算类比的基础上研究性质和运算律。这为学生学习数量积做了很好的
“平面向量数量积的物理背景及其含义”说课稿 宁夏银川唐徕回民中学 马海军 说课内容:普通高中课程标准实验教科书(人教 A 版)《数学必修 4》第 二章第四节“平面向量的数量积”的第一课时-平面向量数量积的物理背景及 其含义。 下面,我从背景分析、教学目标设计、课堂结构设计、教学过程设计、教 学媒体设计及教学评价设计六个方面对本节课的思考进行说明。 一、 背景分析 1、学习任务分析 平面向量的数量积是继向量的线性运算之后的又一重要运算,也是高中数 学的一个重要概念,在数学、物理等学科中应用十分广泛。本节内容教材共安 排两课时,其中第一课时主要研究数量积的概念,第二课时主要研究数量积的 坐标运算,本节课是第一课时。 本节课的主要学习任务是通过物理中“功”的事例抽象出平面向量数量积 的概念,在此基础上探究数量积的性质与运算律,使学生体会类比的思想方法, 进一步培养学生的抽象概括和推理论证的能力。其中数量积的概念既是对物理 背景的抽象,又是研究性质和运算律的基础。同时也因为在这个概念中,既有 长度又有角度,既有形又有数,是代数、几何与三角的最佳结合点,不仅应用 广泛,而且很好的体现了数形结合的数学思想,使得数量积的概念成为本节课 的核心概念,自然也是本节课教学的重点。 2、学生情况分析 学生在学习本节内容之前,已熟知了实数的运算体系,掌握了向量的概念 及其线性运算,具备了功等物理知识,并且初步体会了研究向量运算的一般方 法:即先由特殊模型(主要是物理模型)抽象出概念,然后再从概念出发,在 与实数运算类比的基础上研究性质和运算律。这为学生学习数量积做了很好的

铺垫,使学生倍感亲切。但也正是这些干扰了学生对数量积概念的理解,一方 面,相对于线性运算而言,数量积的结果发生了本质的变化,两个有形有数的 向量经过数量积运算后,形却消失了,学生对这一点是很难接受的:另一方面, 由于受实数乘法运算的影响,也会造成学生对数量积理解上的偏差,特别是对 性质和运算律的理解。因而本节课教学的难点数量积的概念。 二、教学目标设计 《普通高中数学课程标准(实验)》对本节课的要求有以下三条: (1)通过物理中“功”等事例,理解平面向量数量积的含义及其物理意义。 (2)体会平面向量的数量积与向量投影的关系。 (3)能用运数量积表示两个向量的夹角,会用数量积判断两个平面向量的 垂直关系。 从以上的背景分析可以看出,数量积的概念既是本节课的重点,也是难点。 为了突破这一难点,首先无论是在概念的引入还是应用过程中,物理中“功” 的实例都发挥了重要作用。其次,作为数量积概念延伸的性质和运算律,不仅 能够使学生更加全面深刻地理解概念,同时也是进行相关计算和判断的理论依 据。最后,无论是数量积的性质还是运算律,都希望学生在类比的基础上,通 过主动探究来发现,因而对培养学生的抽象概括能力、推理论证能力和类比思 想都无疑是很好的载体。 综上所述,结合“课标”要求和学生实际,我将本节课的教学目标定为: 1、了解平面向量数量积的物理背景,理解数量积的含义及其物理意义: 2、体会平面向量的数量积与向量投影的关系,掌握数量积的性质和运算律, 并能运用性质和运算律进行相关的运算和判断:
铺垫,使学生倍感亲切。但也正是这些干扰了学生对数量积概念的理解,一方 面,相对于线性运算而言,数量积的结果发生了本质的变化,两个有形有数的 向量经过数量积运算后,形却消失了,学生对这一点是很难接受的;另一方面, 由于受实数乘法运算的影响,也会造成学生对数量积理解上的偏差,特别是对 性质和运算律的理解。因而本节课教学的难点数量积的概念。 二、 教学目标设计 《普通高中数学课程标准(实验)》 对本节课的要求有以下三条: (1)通过物理中“功”等事例,理解平面向量数量积的含义及其物理意义。 (2)体会平面向量的数量积与向量投影的关系。 (3)能用运数量积表示两个向量的夹角,会用数量积判断两个平面向量的 垂直关系。 从以上的背景分析可以看出,数量积的概念既是本节课的重点,也是难点。 为了突破这一难点,首先无论是在概念的引入还是应用过程中,物理中“功” 的实例都发挥了重要作用。其次,作为数量积概念延伸的性质和运算律,不仅 能够使学生更加全面深刻地理解概念,同时也是进行相关计算和判断的理论依 据。最后,无论是数量积的性质还是运算律,都希望学生在类比的基础上,通 过主动探究来发现,因而对培养学生的抽象概括能力、推理论证能力和类比思 想都无疑是很好的载体。 综上所述,结合“课标”要求和学生实际,我将本节课的教学目标定为: 1、了解平面向量数量积的物理背景,理解数量积的含义及其物理意义; 2、体会平面向量的数量积与向量投影的关系,掌握数量积的性质和运算律, 并能运用性质和运算律进行相关的运算和判断;
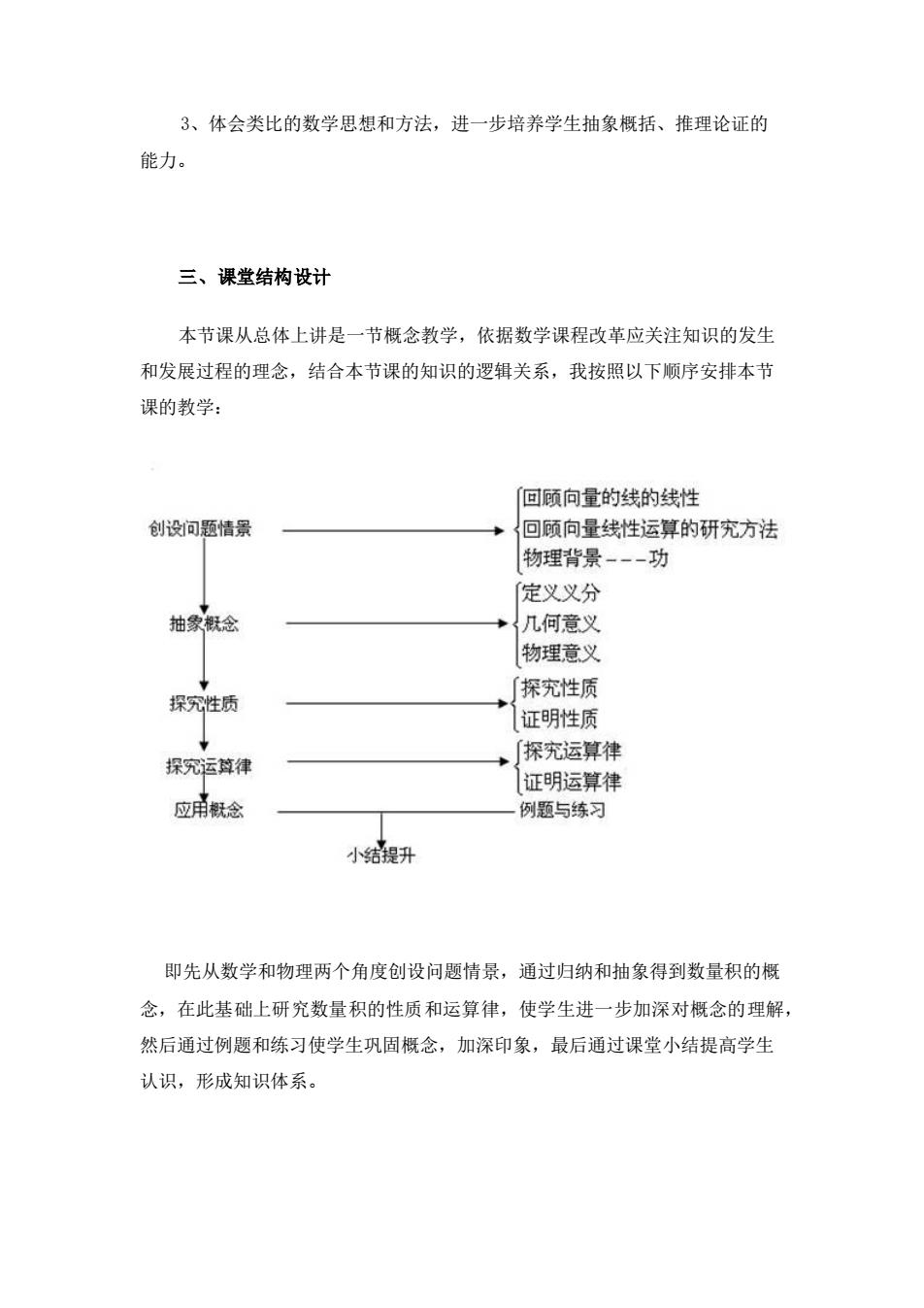
3、体会类比的数学思想和方法,进一步培养学生抽象概括、推理论证的 能力。 三、课堂结构设计 本节课从总体上讲是一节概念教学,依据数学课程改革应关注知识的发生 和发展过程的理念,结合本节课的知识的逻辑关系,我按照以下顺序安排本节 课的教学: 回顾向量的线的线性 创设问题情景 回顾向量线性运算的研究方法 物理背景-功 「定义义分 抽象概念 +几何意义 物理意义 ∫探究性质 探究性质 证明性质 探究运算律 ∫探究运算律 证明运算律 应角献念 例题与练习 小结提升 即先从数学和物理两个角度创设问题情景,通过归纳和抽象得到数量积的 念,在此基础上研究数量积的性质和运算律,使学生进一步加深对概念的理解, 然后通过例题和练习使学生巩固概念,加深印象,最后通过课堂小结提高学生 认识,形成知识体系
3、体会类比的数学思想和方法,进一步培养学生抽象概括、推理论证的 能力。 三、课堂结构设计 本节课从总体上讲是一节概念教学,依据数学课程改革应关注知识的发生 和发展过程的理念,结合本节课的知识的逻辑关系,我按照以下顺序安排本节 课的教学: 即先从数学和物理两个角度创设问题情景,通过归纳和抽象得到数量积的概 念,在此基础上研究数量积的性质和运算律,使学生进一步加深对概念的理解, 然后通过例题和练习使学生巩固概念,加深印象,最后通过课堂小结提高学生 认识,形成知识体系

四、教学媒体设计 和“大纲”教材相比,“课标”教材在本节课的内容安排上,虽然将向量 的夹角在“平面向量基本定理”一节提前做了介绍,但却将原来分两节课完成 的内容合并成一节,相比较而言本节课的教学任务加重了许多。为了保证教学 任务的完成,顺利实现本节课的教学目标,考虑到本节课的实际特点,在教学 媒体的使用上,我的设想主要有以下两点: 1、制作高效实用的电脑多媒体课件,主要作用是改变相关内容的呈现方式, 以此来节约课时,增加课堂容量。 2、设计科学合理的板书(见下),一方面使学生加深对主要知识的印象, 另一方面使学生清楚本节内容知识间的逻辑关系,形成知识网络。 平面向量数量积的物理背景及其含义 一、数量积的概念 二、数量积的性 质 四、应用与提高 1、概 : 例1: 2、概念强调(1)记 法 例2: (2)“规定” 三、数量积的运算 例3: 3、几何意义: 4、物理意义:
四、 教学媒体设计 和“大纲”教材相比,“课标”教材在本节课的内容安排上,虽然将向量 的夹角在“平面向量基本定理”一节提前做了介绍,但却将原来分两节课完成 的内容合并成一节,相比较而言本节课的教学任务加重了许多。为了保证教学 任务的完成,顺利实现本节课的教学目标,考虑到本节课的实际特点,在教学 媒体的使用上,我的设想主要有以下两点: 1、制作高效实用的电脑多媒体课件,主要作用是改变相关内容的呈现方式, 以此来节约课时,增加课堂容量。 2、设计科学合理的板书(见下),一方面使学生加深对主要知识的印象, 另一方面使学生清楚本节内容知识间的逻辑关系,形成知识网络。 平面向量数量积的物理背景及其含义 一、 数量积的概念 二、数量积的性 质 四、应用与提高 1、 概 念: 例 1: 2、 概念强调 (1)记 法 例 2: (2)“规定” 三、数量积的运算 律 例 3: 3、几何意义: 4、物理意义:

五、教学过程设计 课标指出:数学教学过程是教师引导学生进行学习活动的过程,是教师和 学生间互动的过程,是师生共同发展的过程。为有序、有效地进行教学,本节 课我主要安排以下六个活动: 活动一:创设问题情景,激发学习兴趣 正如教材主编寄语所言,数学是自然的,而不是强加于人的。平面向量的 数量积这一重要概念,和向量的线性运算一样,也有其数学背景和物理背景, 为了体现这一点,我设计以下几个问题: 问题1:我们已经研究了向量的哪些运算?这些运算的结果是什么? 问题2:我们是怎么引入向量的加法运算的?我们又是按照怎样的顺序研 究了这种运算的? 期望学生回答:物理模型→概念→性质→运算律→应用 问题3:如图所示,一物体在力F的作用下产生位移S
五、 教学过程设计 课标指出:数学教学过程是教师引导学生进行学习活动的过程,是教师和 学生间互动的过程,是师生共同发展的过程。为有序、有效地进行教学,本节 课我主要安排以下六个活动: 活动一:创设问题情景,激发学习兴趣 正如教材主编寄语所言,数学是自然的,而不是强加于人的。平面向量的 数量积这一重要概念,和向量的线性运算一样,也有其数学背景和物理背景, 为了体现这一点,我设计以下几个问题: 问题 1:我们已经研究了向量的哪些运算?这些运算的结果是什么? 问题 2:我们是怎么引入向量的加法运算的?我们又是按照怎样的顺序研 究了这种运算的? 期望学生回答:物理模型→概念→性质→运算律→应用 问题 3:如图所示,一物体在力 F 的作用下产生位移 S