
西北农林科技大学 emistne 生物在,司 动物科技学院生物化学课程组 第三节酶任反应动力学
生物 化学 动物科技学院生物化学课程组 西北农林科技大学 第三节 酶促反应动力学

生物 化学 第三节醉任反定动力学 酶反寇动力学 概述 主要研究酶催化的反应速度以及影响 底物浓度 反应速度的各种因素。 3 酶浓度 影响酶促化学反应的因素很多,主要 4 温度 有底物浓度、酶浓度、温度、pH、抑制 pH 剂、激活剂等。 6 抑制剂 在探讨各种因素对酶促反应速度的影 激活剂 响时,通常测定其初始速度来代表酶促 反应速度,即底物转化量<5%时的反应 速度
生物 化学 第三节 酶促反应动力学 酶反应动力学 主要研究酶催化的反应速度以及影响 反应速度的各种因素。 影响酶促化学反应的因素很多,主要 有底物浓度、酶浓度、温度、pH、抑制 剂、激活剂等。 在探讨各种因素对酶促反应速度的影 响时,通常测定其初始速度来代表酶促 反应速度,即底物转化量<5%时的反应 速度。 概 述 pH 抑制剂 温度 酶浓度 激活剂 底物浓度 1 3 5 7

第三节酵任反定动力学 概述 2底物浓度 Michaelis Menten 1913 动力学曲线 年拟合出了该双曲线的表达式, 即著名的米氏方程 2 米氏方程 Km的意义 Km与Vmax (3)zero order 3 酶浓度 V max/2 Vmax (2)mixe [S] 4 温度 Km+ [S1 5 pH ()1 st order m即为米氏常数, 6 抑制剂 0 max为最大反应速度 激活剂 J
生物 化学 第三节 酶促反应动力学 酶促反应动力学曲线 概 述 pH 抑制剂 温度 酶浓度 激活剂 Km与Vmax 动力学曲线 米氏方程 Km的意义 底物浓度 Michaelis & Menten 于1913 年拟合出了该双曲线的表达式, 即著名的米氏方程 V= Vmax [S] Km + [S] Km 即为米氏常数, Vmax为最大反应速度 1 3 5 7 (1) (2) (3) (4)
生物 化 VIS 概述 反应初速 底物浓县 VISI 若V=V/2 动力学虽 Km+[S] 米氏方 Km的 4 Km与Vm [ST 酶浓度 Km [S] m -S1 温度 ph Km+&]-=[S 6 抑制剂 激活剂 Km 米氏曲线
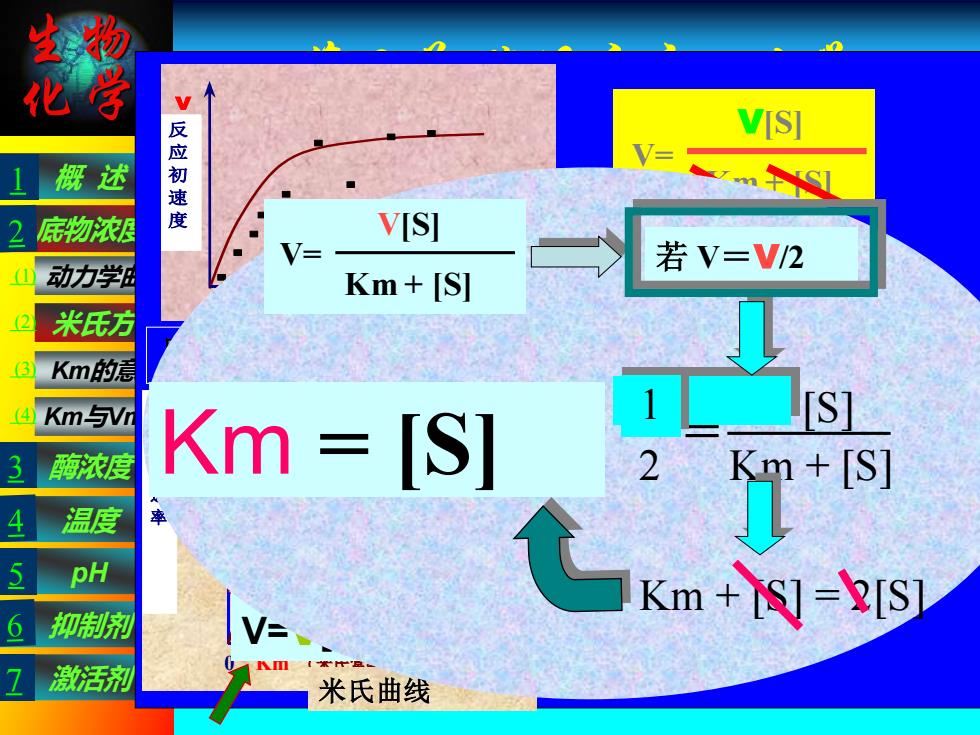
生物 化学 第三节 酶促反应动力学 米氏方程的推导 理论根据:“稳态平衡”假说(恒态假说) 该假说认为酶促反应分两步: 概 述 pH 抑制剂 温度 酶浓度 激活剂 Km与Vmax 动力学曲线 米氏方程 Km的意义 底物浓度 E+S ES E+P K1 K2 K3 K4 中 间 产物 产物 ① ② 第一步为可逆的快速反应,第二步为慢速反应,整个 反应速度取决于反应最慢的第二步;在反应中既有ES 的生成又有ES的分解;在反应的初始阶段,随着ES浓 度的升高ES的分解速度也随之增大,直到一个平衡点 使得ES的生成速度等于ES的分解速度,从而使ES的 浓度达到一个恒态。这是总反应的速度等于ES分解为 产物和游离酶的速度。 考虑ES的形成速度 因为E+P-→ ES 的速度极小,可忽略不计 ES的形成速度d[ES]/dt = K1([E0]-[ES])·[S] ③ [E0]-- 酶的总浓度 [ES]-- 酶与底物形成的中间产物的浓度 [E0]-- [ES]为游离状态的酶的浓度 [S]-- 底物的浓度 [S]>>[E0]时,被酶结合的S量,即[ES],与总 的底物浓度相比,可忽略不计 [S]-[ES] ≈ [S] E +S ES P+ E K1 K4 ES ES的分解速度 此两式速度之和为ES分解的总速度 -d[ES]/dt = K2[ES]+K3[ES] ④ 当酶反应体系处于动态平衡(恒态)时 ES的形成速度 = ES分解速度 [ES]保持动态的恒定 ⑶ = ⑷ 即:K1([E0]-[ES])·[S] = K2[ES]+K3[ES] ([E0]-[ES])·[S] / [ES] = (K2+K3) / K1 ⑤ ES E +S E + P K2 K3 ES 令:Km = (K2+K3) / K1 代入⑤ 则 ([E0]-[ES])·[S] / [ES] = Km ⑥ ∴动态平衡时的[ES]: [ES] = [E0][S] / (Km+[S]) ⑦ 由于酶的反应速度(v)与[ES]成正比 ∴ v = K3[ES] ⑧ 将⑦的[ES]代入⑧得: v = K3·[E0][S] / Km+[S] ⑨ 当底物浓度很高时,所有的酶都被底物所饱和, 而转变成ES复合物,即[E0] = [ES]时,酶促 反应达到最大速度 ∴ Vmax = K3[ES] = K3[E0] ⑩ ⑨除以⑩: v/Vmax = K3[E0][S] / (Km+[S]) / K3[E0] ∴ v = Vmax[S] / (Km+[S]) 米氏方程反映:已知Km、Vmax、v与底物 浓度之间的定量关系 Km--米氏常数 V 0 底 物 浓 度 [S] 反 应 初 速 度 反应初速度随底物浓度变化曲线 V V V/2 0 Km (米氏常数) [S] 最 大 反 应 速 率 米氏曲线 b.当[S]很大时 V=V[S]/[S]=V 0 级反应 混合级 a.当[S]很小时 V=V[S]/Km 一级反应 V= V[S] Km + [S] Km = [S] 若 V=V/2 V 2 = V [S] Km + [S] 1 Km + [S] = 2[S] V= V[S] Km + [S] 1 3 5 7 (1) (2) (3) (4)

第三节酵钱反寇动力学 概述 3.K是酵的特征性常款,可用来判断醉 2 底物浓度 的景造底物: 在一定条件下,某种酶的Km 动力学曲线 值是恒定的,因而可以通过测定不同酶(特 (2 米氏方程 别是一组同工酶)的K值,来判断是否为 Km的意叉 不同的酶。 Km与Vmax 当酶有几种不同的底物存在时,通过测 3 酶浓度 定酶在不同底物存在时的Km值,Km值最小 4 温度 者,即为该酶的最适底物。 5 pH Vmax可用于汁养膝的希换款:当酶的总 6 抑制剂 浓度和最大速度已知时,可计算出酶的转换 数,即单位时间内每个酶分子催化底物转变 激活剂 为产物的分子数
生物 化学 第三节 酶促反应动力学 Km和Vmax的意义 1.当ν=Vmax/2时,Km=[S]。因此,Km 等于酶促反应速度达最大值一半时的底 物浓度。 概 述 pH 抑制剂 温度 酶浓度 激活剂 Km与Vmax 动力学曲线 米氏方程 Km的意义 底物浓度 Km≈k2/k1 E + S ES P + E k1 k2 k3 Km越小,亲和力越强。底物浓度很 小时,反应速度就能达到很大,性能优,代谢中这 类酶更为重要。 当k2>>k3时(通常都是这样) 2. Km可以反映酶与底物亲和力的大小 Km= k2 + k3 k1 3. Km是酶的特征性常数,可用来判断酶 的最适底物:在一定条件下,某种酶的Km 值是恒定的,因而可以通过测定不同酶(特 别是一组同工酶)的Km值,来判断是否为 不同的酶。 当酶有几种不同的底物存在时,通过测 定酶在不同底物存在时的Km值,Km值最小 者,即为该酶的最适底物。 4.Vmax可用于计算酶的转换数:当酶的总 浓度和最大速度已知时,可计算出酶的转换 数,即单位时间内每个酶分子催化底物转变 为产物的分子数。 1 3 5 7 (1) (2) (3) (4)