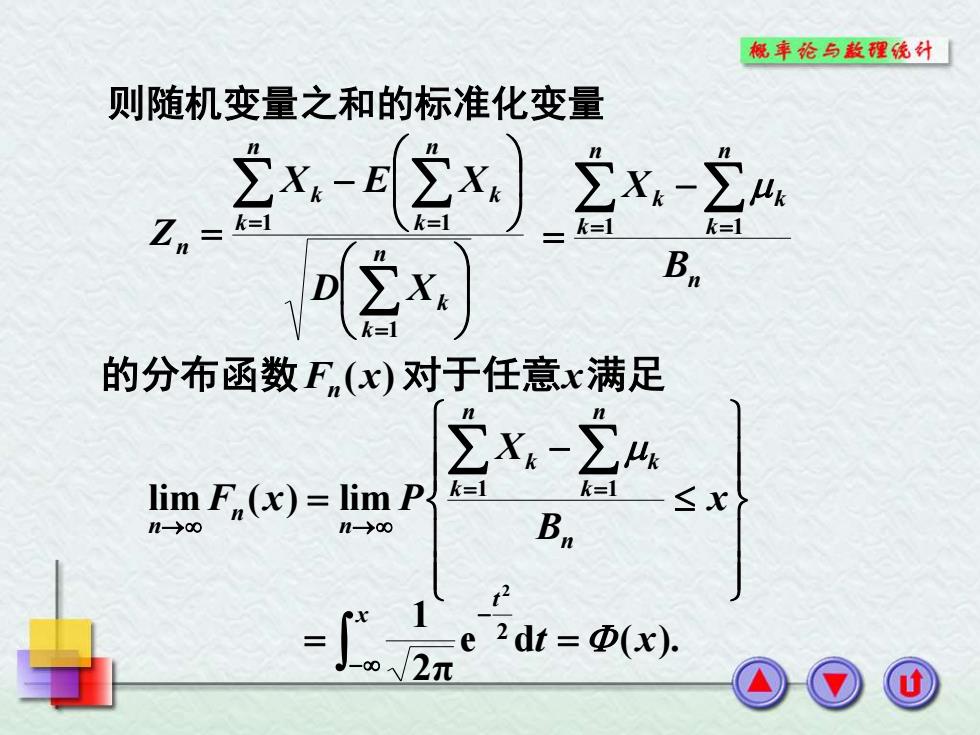
概率伦与款醒统外「 则随机变量之和的标准化变量 x-2x2x-24 k=1 2x B 的分布函数F(x)对于任意x满足 ∑x-∑4 lim F((x)=lim P每 k=1 ≤X〉
则随机变量之和的标准化变量 − = = = = n k k n k k n k k n D X X E X Z 1 1 1 n n k k n k k B X = = − = 1 1 的分布函数Fn (x)对于任意x满足 − = = = → → x B X F x P n n k k n k k n n n 1 1 lim ( ) lim − − = = x t e dt (x). 2π 1 2 2

概车纶与款理统外 定理五表明: 无论各个随机变量X1,X2,.,Xm,.服从什么 分布,只要满足定理的条件,那么它们的和∑X。 k=1 当n很大时,近似地服从正态分布. (如实例中射击偏差服从正态分布) 下面介绍的定理六是定理四的特殊情况
定理五表明: , . , , , , , , 1 1 2 当 很大时 近似地服从正态分布 分布 只要满足定理的条件 那么它们的和 无论各个随机变量 服从什么 n X X X X n k k n = (如实例中射击偏差服从正态分布) 下面介绍的定理六是定理四的特殊情况

概華论与款醒硫外 定理六(德莫佛一拉普拉斯定理) 德莫佛 拉普拉斯 设随机变量nn(n=1,2,)服从参数为n,p (0<p<1)的二项分布,则对于任意x,恒有 Ps小上2ar-ow 证明 根据第四章第二节例题可知,=∑X, k=1 其中X1,X2,.,Xn是相互独立的、服从同一 (0一1)分布的随机变量,分布律为 PXk=i}=p(1-p)-, i=0,1
− − → = = − − = x t n n n x t x np p np P p x n n p e d ( ). 2π 1 (1 ) lim (0 1) , , ( 1,2, ) , 2 2 的二项分布 则 对于任意 恒有 设随机变量 服从参数为 证明 根据第四章第二节例题可知 , 1 = = n k n Xk - 分布的随机变量 分布律为 其中 是相互独立的、服从同一 (0 1) , , , , X1 X2 Xn { } (1 ) , 0, 1. 1 = = − = − P X i p p i i i k 定理六(德莫佛-拉普拉斯定理) 德莫佛 拉普拉斯

概车纶与款理统外「 .E(Xk)=p,D(Xk)=p(1-p)(k=1,2,.,n), 根据定理四得 e 2dt =(x). 定理六表明: 正态分布是二项分布的极限分布,当n充分大 时,可以利用该定理来计算二项分布的概率
E(X ) p, k = D(X ) p(1 p) (k 1,2, ,n), k = − = 根据定理四得 = − − → x np p np P n n (1 ) lim − − = → x np p X np P n k k n (1 ) lim 1 − − = = x t e dt (x). 2π 1 2 2 定理六表明: 正态分布是二项分布的极限分布, 当n充分大 时, 可以利用该定理来计算二项分布的概率