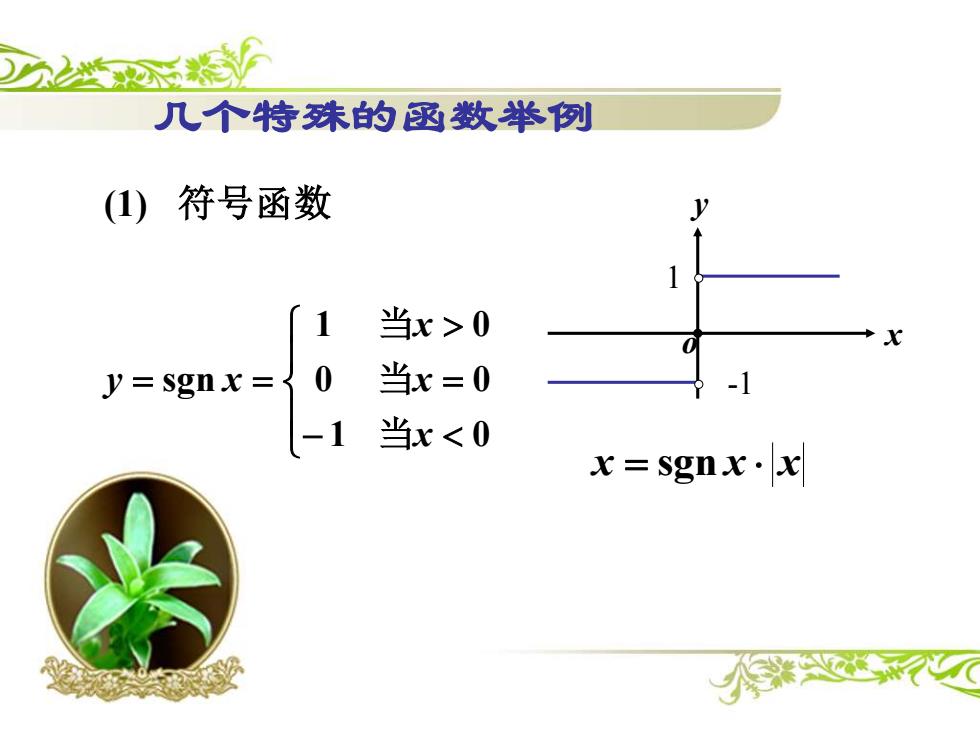
几个恃殊的函数举例 (1)符号函数 1 当x>0 y=sgnx= 当x=0 -1 当x<0 x=Sgnx·x
(1) 符号函数 − = = = 1 0 0 0 1 0 sgn x x x y x 当 当 当 几个特殊的函数举例 1 -1 x y o x = sgn x x

(2)取整函数y=x x表示不超过x的最大整数 d ●0 4-3-2-1.0112345x 23 .4 阶梯曲线
(2) 取整函数 y=[x] [x]表示不超过x 的最大整数 1 2 3 4 5 -2 -4 -4 -3 -2 -1 4 3 2 1 -1 -3 x y o 阶梯曲线
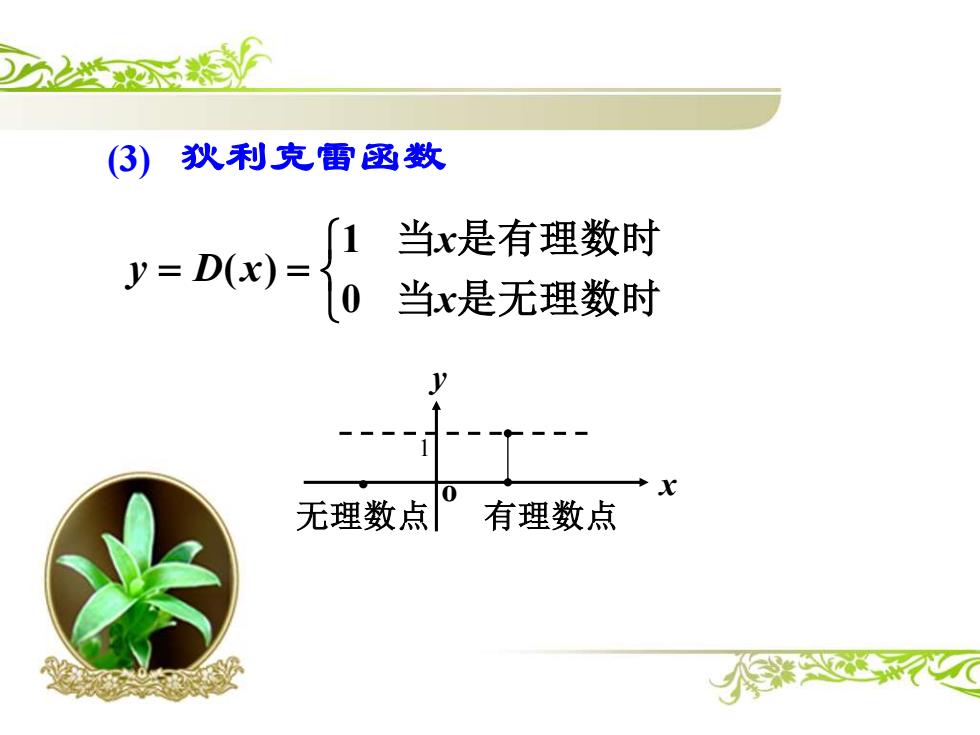
3) 狄利克雷函数 [1当x是有理数时 y=D(x)= 0 当x是无理数时 y 无理数点有理数点 米兴《
= = 当 是无理数时 当 是有理数时 x x y D x 0 1 ( ) 无理数点 有理数点 • 1 x y o (3) 狄利克雷函数
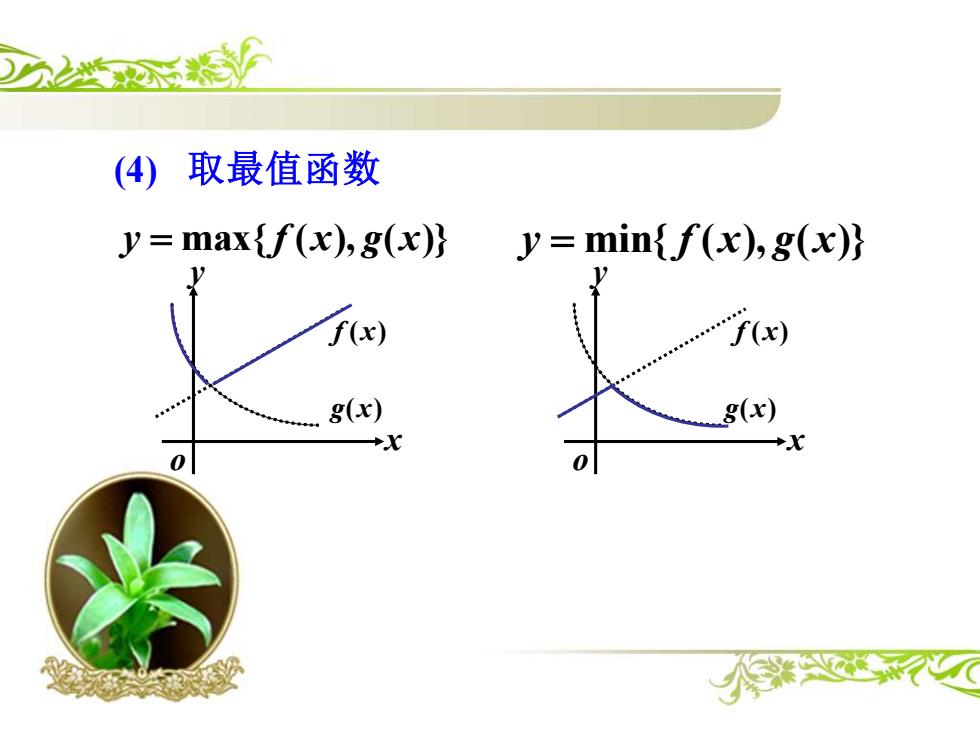
(4)取最值函数 y=maxif(x),g(x)} y=min{f(x),g(x) f(x) "f(x) g(x) 8(x) +0 0
(4) 取最值函数 y = max{f (x), g(x)} y = min{ f (x), g(x)} y x o f (x) g(x) y x o f (x) g(x)

在自变量的不同变化范围中,对应法则用不同的 式子来表示的函数,称为分段函数 2x-1,x>0 例如,f(x)= x2-1,x≤0 y=x2-1 y=2x-1
− − = 1, 0 2 1, 0 , ( ) 2 x x x x 例如 f x 1 y = 2x − 1 2 y = x − 在自变量的不同变化范围中,对应法则用不同的 式子来表示的函数,称为分段函数