
△E=R1( n 当n,=1,n2=o时,△E=2.179×10-18J, AE-the ionization energy of a hydrogen atom (氢原子的电离能) △E=hv v=3.289×105(日) 3.289×105=2.179×10-18 h It can be seen that the meaning of the constant is the quotient of ionization energy divided by the Planck constant
) 1 1 ( 2 2 2 1 H n n E = R − h 1 8 1 5 2.179 10 3.289 10 − = ) 1 1 1 3.289 10 ( 2 2 1 5 E = h = − E − the ionization energy of a hydrogen atom. 当n1 =1,n2 = 时,E = 2.17910−1 8 J, (氢原子的电离能 ) the quotient of ionization energy divided by the Planck constant。 It can be seen that the meaning of the constant is

The difference in energy (AE)between energy levels n and △E。=E。-E=hm=h×3289×105-1 2.179×1018 Eorbital energy of the n orbital for an electron Regulation(规定):(Ec=O) n一quantum number(量子数) En、 2.179×1018 Calculation of energy of specified orbits of the H atom E.g:the transfer energy between 4th orbital and 2ed orbital: =么-公=-2179x10"华是-408610J Hs V= △E4.086×1019 6.626×104=6.167×104 1==3.0x107 =486.5nm h 6.167×104
E E E hv n = − n = -1 2 2 1 5 s 1 1 3.289 10 = − n h En—— orbital energy of the orbital for an electron n— quantum number (量子数) E.g: the transfer energy between 4th orbital and 2ed orbital: 1 4 1 3 4 1 9 6.167 10 6.626 10 4.086 10 − − − = = = s h E v 486.5nm 6.167 10 3.0 10 14 17 = = = v c Hβ ◆The difference in energy (En ) between energy levels n and Regulation(规定):(E = 0) Calculation of energy of specified orbits of the H atom J 2.179 10 2 18 n − = E E E J 19 2 2 18 4 2 ) 4.086 10 2 1 4 1 - 2.179 10 ( − − = = − − = J 2.179 10 2 18 n En − =
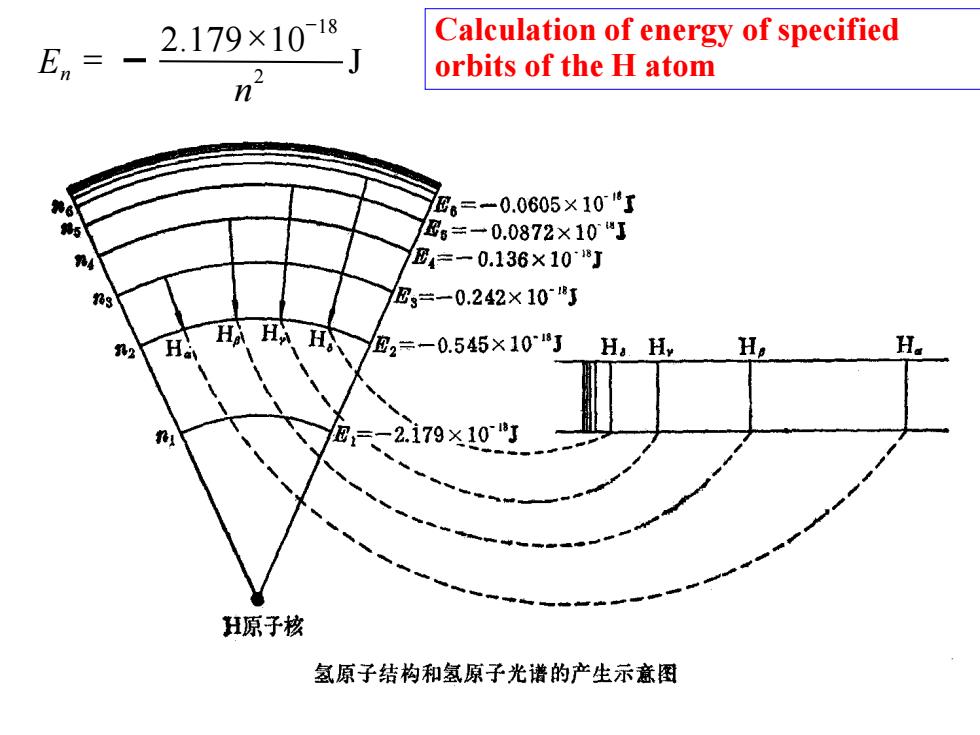
En- 2.179x10」 Calculation of energy of specified orbits of the H atom n E。=-0.0605×10了 ®6=-0.0872×10"J E4=一0.136×108J 9 E3÷一0.242×108J 、H武2=-0.55×10"J Ha H, -2.179×10 H原子核 氢原子结构和氢原子光谱的产生示意图
J 2 .179 10 2 18 n E n − = Calculation of energy of specified orbits of the H atom
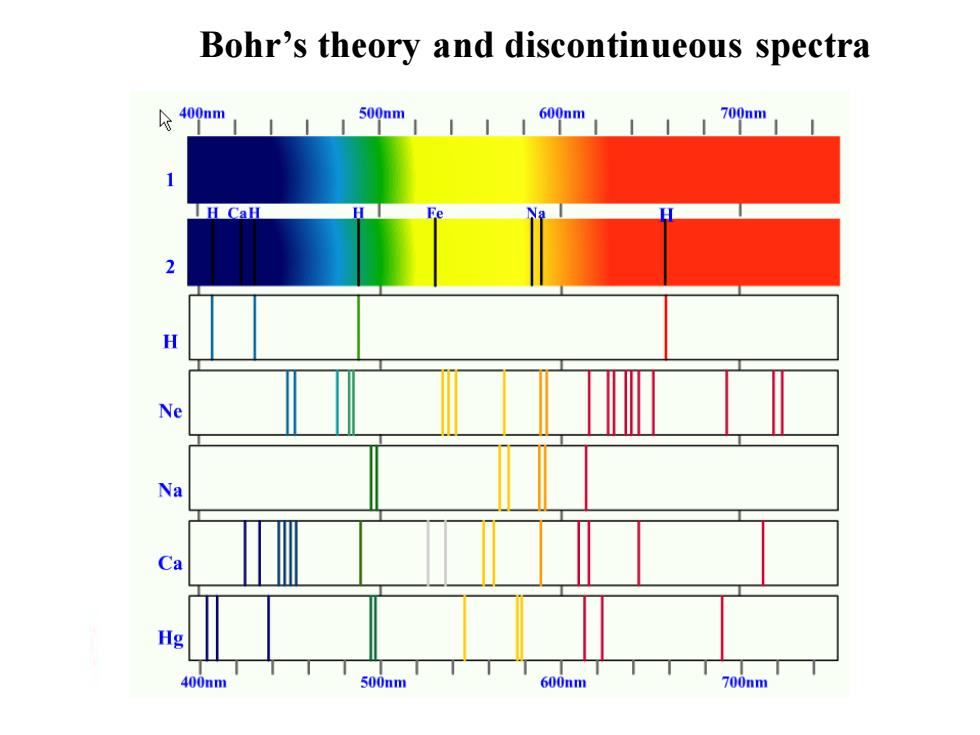
Bohr's theory and discontinueous spectra 令400nm 500nm 600nm 700nm 400nm 500nm 600nm 700nm
Bohr’s theory and discontinueous spectra

8.1.2 The dual nature of the electron In 1925,Louis de Broglie proposed that a free moving electron with mass m and velocity o should have an associated wavelength given by the equation E0mc=h=流=各 h=6.626X 10-34Js,p,Planck's constant In 1927,an electron diffraction experiment with Ni crystal did by Davissson and Germerdid confirms the wave character of electron
In 1925, Louis de Broglie proposed that a free moving electron with mass m and velocity υ should have an associated wavelength given by the equation : 8.1.2 The dual nature of the electron In 1927, an electron diffraction experiment with Ni crystal did by Davissson and Germerdid confirms the wave character of electron h=6.626×10-34J·s,p, Planck’s constant λ= = h mc h E = mc p 2 = h