
·12 绪论 是关于k的i次多项式.当N<1时,A=0.当N≥1时,mA=0不 成立.证毕. 推论m4心=0的一个充分条件是存在范数,使得4训<1. 证明川A川≤川A*-1川I川A|≤川A-2|A2≤.≤川A*.则 IA<1→川Ak→0→‖A‖一0 由范数的性质得 A=0 0.3.3矩阵的条件数 在解方程组时,我们总是假定系数矩阵A和常数项b是准确的,而在实际问题 中,系数矩阵A和常数项b往往是由前面的近似计算所得,元素的误差是不可避免 的.这些误差会对方程组Ax=b的解x有多大的影响?矩阵的条件数给出一种粗 略的衡量尺度 定义0.13若A非奇异,称Cond(A)=IA,A1‖。为A的条件数.其中 l。表示矩阵的某种范数。 Comd(A)≥1,当A为正交矩阵时Cond(A)=1. 注Cond(A)=A-H‖IA≥A-1A|=1Il=1. 用矩阵A及其逆矩阵A-】的范数的乘积表示矩阵的条件数,由于矩阵范数的 定义不同,因而其条件数也不同,但是由于矩阵范数的等价性,故在不同范数下的 条件数也是等价的 对于线性方程组Ax=b,若常数项b有小扰动,设A(z+6z)=b+,6z 受到的影响表示为 哥<cad〔 (0.8) 分析A·6z=66,6z=A-166,6x≤川A-1川I6b: 在=&闭a跳≥岗 所以 图<14a贤=-cm 若系数矩阵有小扰动6A,这时方程组的解也有扰动江,于是 (4+6A)(x+6z)=b

0.3矩阵和向量范数 .13. 6z受到6A的影响表示为 ≤ x 1-caa离 (0.9) 定理0.3设A∈Rn×n,b∈R”,Ax=b,A非奇异,6A和b是A和b的 扰动, A-16A1<1 则 骨(+) 6 (0.10) 矩阵条件数的大小是衡量矩阵“好”或“坏的标志.因此,称Cod(A)大的 矩阵为“坏矩阵”或“病态矩阵”,对于Cod(4)大的矩阵,小的误差可能会引起 解的失真.一般说来,若A的按模最大特征值与按模最小特征值之比值较大时,矩 阵就会呈病态. 例0.7方程组 1.0002x1+0.9998x2=2 0.9998x1+1.0002x2=2 的准确解为 x=(c1,2)T=(1,1)T 对常数项b引入小扰动6=(0.001,-0.001)T,则 1.00020.9998 2.001 0.99981.0002 x2/ 1.999 1250.25-1249.75 A-1= -1249.75 1250.25 故Cond(A)=2.2500=5000, 6xl=2.5, llloo 1=0.001,解的相对误差是右 b例。 端项相对误差的2500倍. 从几何上看,这两个方程是平面上的两条直线,求方程组的解是求两条直线的 交点,条件数大表明这两条直线接近平行,求解中对误差必然敏感

.14 绪论 对常数项b引入小扰动b=(0.0001,-0.0001)T,则 1.0020.998)()=(2001) (+6)=125 0.99981.0002/x2/ 1.9999 x2+62 0.75 对常数项b引入小扰动动=(0.00001,-0.00001)T,则 (a)()-() 1+x1 1.025 2+6x2 0.975 注本节矩阵范数内容可以放在第4章中讲授

第1章插值 什么是插值?简单地说,用给定的未知函数f(x)的若干点的函数值构造近似 函数p(x),称函数(x)为f(x)的插值函数. 在实际问题中f()作为未知函数,通过测量或经验只能得到函数f(x)的一些 离散点的值{(红,f(),i=0,1,·,n:或者函数f(x)的表达式过于复杂而不便 于运算.这时我们需要构造f(x)的近似函数(c).例如,在服装店订做风衣时,选 择好风衣的样式后,服装师量出并记下你的胸围、衣长和袖长等几个尺寸,这几个 尺寸就是风衣函数的插值点数值,在衣料上画出的裁剪线就是服装师构造的插值函 数(x),裁剪水平的差别就在于量准插值点和构造合乎身材的插值函数. 在数学上常用的函数通近的方法有插值和拟合.本章讨论用插值方法构造近似 函数.第2章讨论用拟合逼近函数 定义1.1f)为定义在区间a,上的函数,{o,1,.,n}为a,创上n+1 个互不相同的点,重为给定的某一函数类.若中上有函数(x),满足 p(x)=f(,i=0,1,.,n 则称p(x)为f(z)关于节点{ao,x1,·,xn}在重上的插值函数.称点{xo,d1,. xn}为插值节点:称{(,f(x),i=0,1,.,n}为插值型值点,简称型值点或插值 点,f(x)称为被插函数.在本章中我们约定a=0<c1<·<cm=b, 这样,对函数f(x)在区间[a,上的各种计算,就用对插值函数p(x)的计算 取而代之 构造插值函数需要关心下列问题: ◇插值函数是否存在? ◇插值函数是否唯一? ◇如何表示插值函数? ◇如何估计被值函数(x)与插值函数(x)的误差? 1.1拉格朗日(Lagrange)插值多项式 可对插值函数的类型作多种不同函数的选择,由于代数多项式具有简单和一些 良好的特性,例如,多项式是无穷光滑的,容易计算它的导数和积分.故常选用代数 多项式作为插值函数
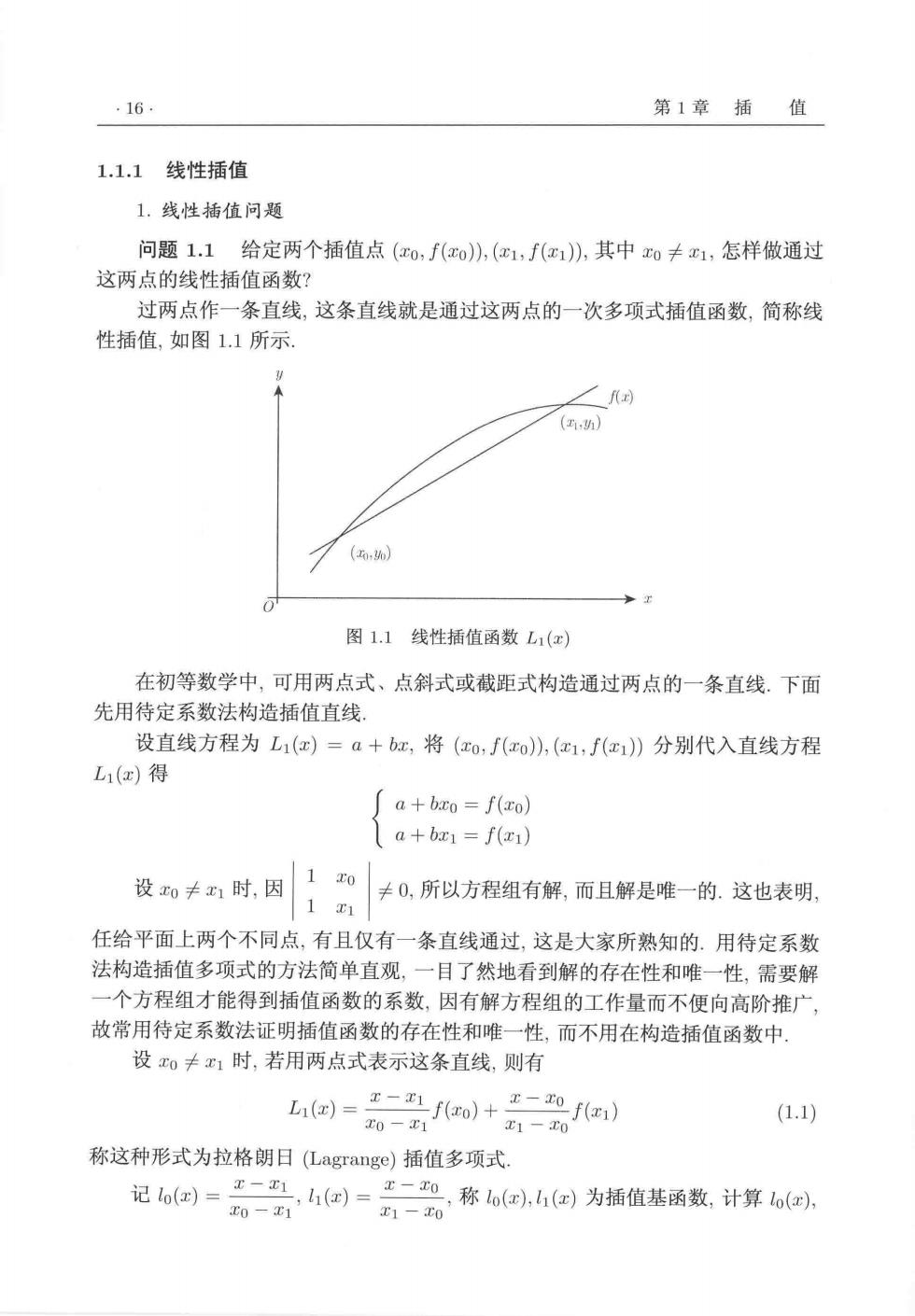
·16 第1章插值 1.1.1线性插值 1.线性插值问题 问题1.1给定两个插值点(co,f(o)》,(c1,f(),其中0≠1,怎样做通过 这两点的线性插值函数? 过两点作一条直线,这条直线就是通过这两点的一次多项式插值函数,简称线 性插值,如图11所示. (】 图1.1线性插值函数L1(x) 在初等数学中,可用两点式、点斜式或截距式构造通过两点的一条直线.下面 先用待定系数法构造插值直线 设直线方程为L1(c)=a+bc,将(xo:f(o),(c1,f(c1)》分别代入直线方程 L1(x)得 a+bxo=f(xo) a+bz1=f(F1) 设0≠时,因}0≠0,所以方程组有解,而且解是唯一的.这也表明, 11 任给平面上两个不同点,有且仅有一条直线通过,这是大家所熟知的.用待定系数 法构造插值多项式的方法简单直观,一目了然地看到解的存在性和唯一性,需要解 一个方程组才能得到插值函数的系数,因有解方程组的工作量而不便向高阶推广 故常用待定系数法证明插值函数的存在性和唯一性,而不用在构造插值函数中, 设0卡x1时,若用两点式表示这条直线,则有 回=二fo)+f 0-x1 (1.1) E1一T0 称这种形式为拉格朗日(Lagrange))插值多项式. 记6=。一4回=二会称4为插值基数计算e