
l.1拉格朗日(Lagrange)插值多项式 17. 41(x)的值,易见 =-{k (1.2) 在Le插值多项式中可将因看作两条直线会一 20-x1 的叠加,可以看到两个插值点的地位和作用都是平等的 拉格朗日插值多项式形式免除了解方程组的计算,易于向高次插值多项式形式 推广 2.线性插值误差 定理1.1记L1(回)为以{o,f(o》,(c1,f)》为插值点的插值函数,0 x1∈[a,0≠x1,设f(x)一阶连续可导,f"(x)在(a,b)上存在,则对任意给定的 x∈[a,至少存在一点∈a,使 R()=f(r)-L()=(r-mo)(t-m1).EF (1.3) 2! 证明令R(ar)=f(x)-L1(r).因R(xo)=R(r1)=0,xo,1是R(x)的根 可设 R(x)=k(x)(x-xo)(x-1) 对任何一个固定的点x,引进辅助函数(), p()=f)-L1()-k(x)t-xo)t-x) 则p()=0,i=0,1. 由定义可得p口)=0,这样p()至少有3个零点,不失一般性,假定0<x< x1,分别在[o,x和z,x]上应用Rolle定理,可知p()在每个区间至少存在一 个零点,不妨记为5和52,即(51)=0和p(52)=0,对()在[51,l上应用 Roe定理,得到p"()在[51,包上至少有一个零点6p"(S)=0. 对()求二次导数,其中”()=0,有 "(t)=f"(t)-2k(x) 代入,得"9)-2()=0,所以=但 2 国=9e-oe-.5eo,l 2 对于不同的x,£的值一般也不相同,即=(x). 定理1.1给出了线性插值的截断误差,插值函数的截断误差也称余项
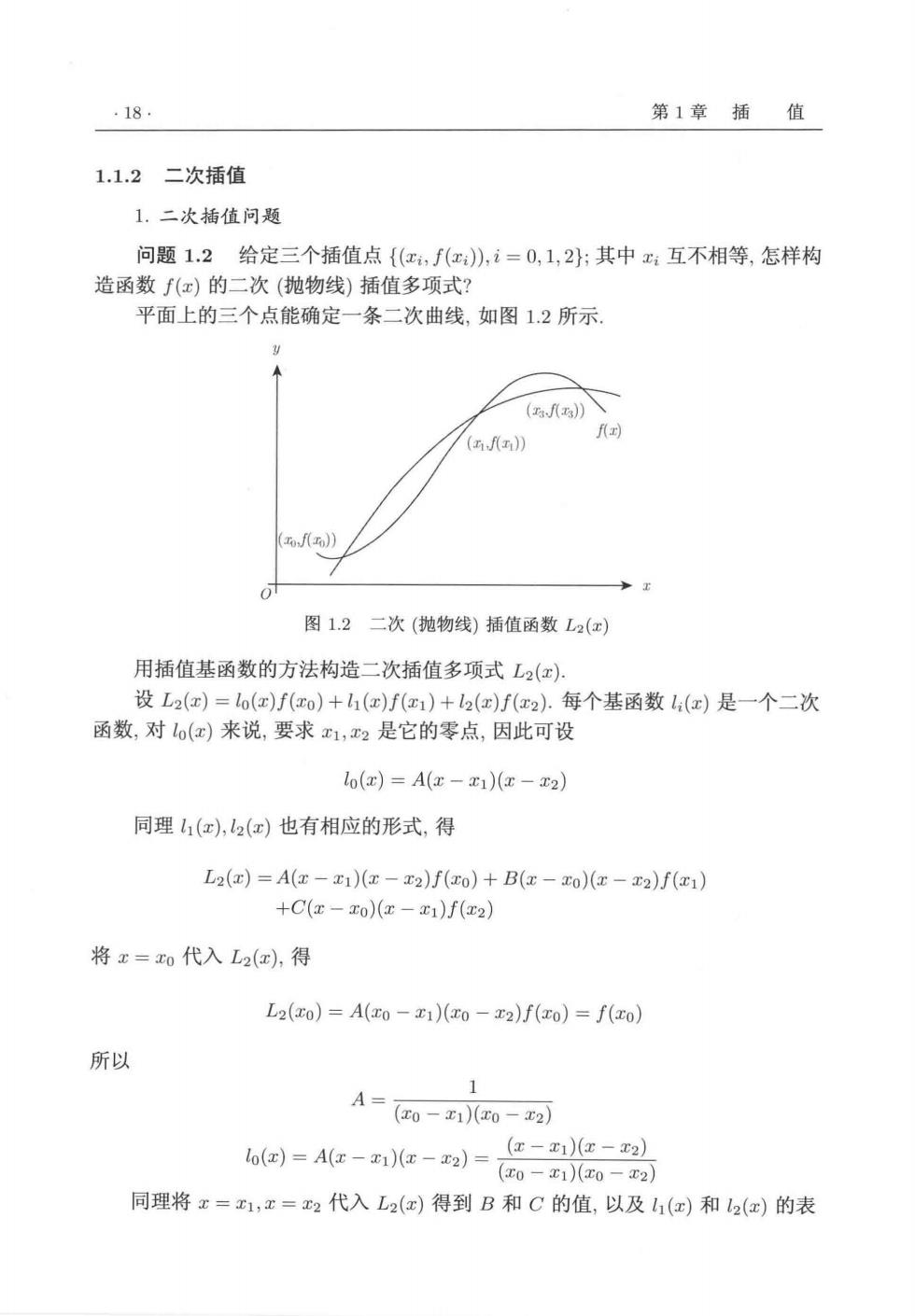
·18 第1章插值 1.1.2二次插值 1.二次插值问题 问题12给定三个插值点{(x,f(x),i=0,1,2:其中互不相等,怎样构 造函数f(x)的二次(抛物线)插值多项式? 平面上的三个点能确定一条二次曲线,如图1.2所示 (》 () 图1.2二次(抛物线)插值函数L2(x) 用插值基函数的方法构造二次插值多项式L2(x), 设L2(x)=lo(x)f(xo)+h(c)f(1)+l2(x)f(r2).每个基函数l:(c)是一个二次 函数,对lo()来说,要求1,2是它的零点,因此可设 l0(x)=A(x-E1)(x-E2) 同理1(x),2(x)也有相应的形式,得 L2(x)=A(z-1)(x-x2)f(xo)+B(z-20)(z-z2)f(z1) +C(x-0)(e-E1)f(x2) 将x=o代入L2(e),得 L2(xo)=A(co-1)(xo-x2)f(xo)=f(ro) 所以 1 A=0-10- =Ae-e-小-货-, 同理将x=1,x=2代入L2(x)得到B和C的值,以及1(e)和12(a)的表

l.1拉格朗日(亿agrange))插值多项式 .19 达式 1 1 B=m1-0j1-2 C=2-02- 多 (-x0)-2】 得到 (x-0)(x-x2) +岳,动园 (1.4) 容易验证插值基函数仍然满足 4=南-{位图 2.二次插值函数误差 l回=f9e-oe-e-2l. 31 (1.5) ξ∈min{zo,t1,x2,x,max{a0,x1,x2,x 上式证明完全类似于线性插值误差的证明,故从略。 插值作为函数逼近方法,常用于函数的近似计算.当计算点落在插值点区间之 内叫做内插,否则叫做外插。内插的效果一般优于外插 例1.1如图1.3所示,给定sin11°=0.190809,sin12°=0.207912,sin13°= 0.224951.构造二次插值函数并计算sin1130. 解 L2(x)= 品=801+品=品0am9e (x-11)(x-12) +03-1m3-12 .224951 L2(11.5)=0.199369,准确值sin1130=0.199368. 更一般地用弧度作为自变量构造插值函数,易估计误差, (11°,12°,13)=(0.191986,0.20944,0.226893)
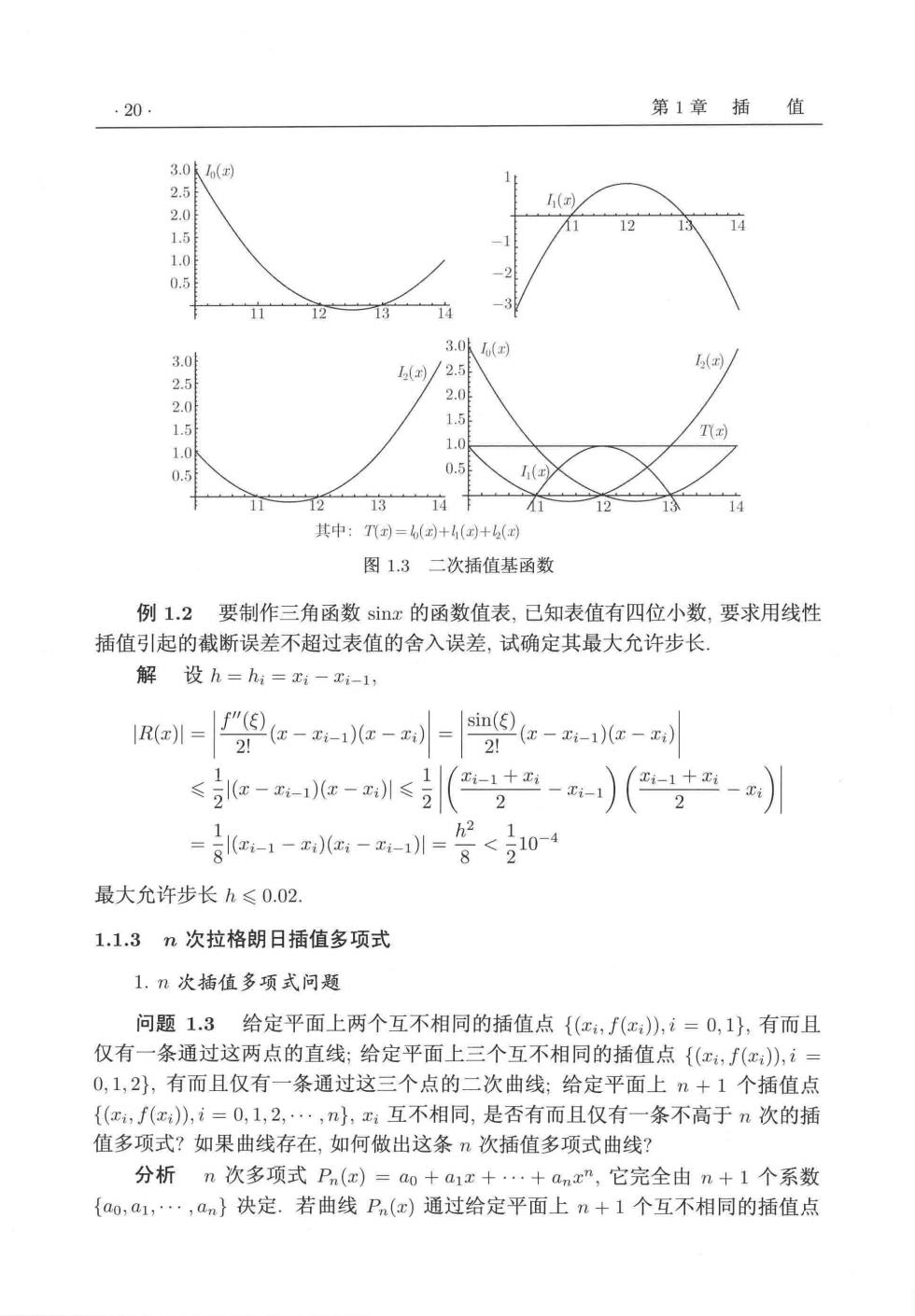
·20 第1章插值 3.0k 2.0 1 1.0 3 14 3.0 3.0(到 2.5 4/2.5 2.0 2.0 1.5 15 .0 0.5 I(z 11 3 12 1 14 其中:T)=+4(国+( 图1.3二次插值基函数 例1.2要制作三角函数six的函数值表,已知表值有四位小数,要求用线性 插值引起的截断误差不超过表值的舍入误差,试确定其最大允许步长 解设h=h=一x-l, 2 2 h2 =e-16-训=<0 最大允许步长h≤0.02. 1.1.3n次拉格朗日插值多项式 1.n次插值多项式问题 问题1.3给定平面上两个互不相同的插值点{(,f(),i=0,1,有而且 仅有一条通过这两点的直线:给定平面上三个互不相同的插值点{(,f(x),i 0,1,2},有而且仅有一条通过这三个点的二次曲线:给定平面上n+1个插值点 {(,f(x),i=0,1,2,·,n},x互不相同,是否有而且仅有一条不高于n次的插 值多项式?如果曲线存在,如何做出这条n次插值多项式曲线? 分析n次多项式Pn()=ag+a1x十.+anxn,它完全由n+1个系数 {ao,a1,·,an}决定.若曲线Pn(x)通过给定平面上n+1个互不相同的插值点

1.1拉格朗日(Lagrange)插值多项式 21 {(e,f(x),i=0,1,.,n,则P(c)满足{P()=f),i=0,1,2,.,n小,事 实上一个插值点就是一个插值条件. 将{(c,f(x),i=0,1,2,.,n}依次代入P(x)中得到线性方程组 a0+a1x0+a2x哈+·+anx0=f(xo) ao+ar+a2x?+.+anti=f(r1) (1.6) a0+a1n+a2x品+.+anxh=f(xn) 方程组的系数行列式是范德蒙(Vandermonde)行列式 10x哈·哈 V(x0,x1,.,tn)= 11号. Π(-x) 0j<i 1xmx品.h 当互异时,Ⅱ(-)≠0,方程组(1.6)的解存在唯一.即问题1.3的 0≤j<6n 解存在而且唯一 通过求解(1.6)得到插值多项式P(x),因其计算量太大而不可取,下面用La grange基函数,构造n次Lagrange插值多项式. 对于n+1个互不相同的插值节点{(,fx)》,i=0,1,2,.,n小,由n次插 值多项式的唯一性,可对每个插值节点作出相应的n次插值基函数{几,(x),i 0,1,2,.,n},要求 e)=时={0,i≠j 了1,i=j {x0,1,.,-,+1,.,n}是(x)零点,因此可设 l(x)=a(x-xo)(e-x1).(e-x-1)(x-E+1).(x-xn) 由:()=1,将x=x,代入l(x)得到 li()=a(m-o)ei-x1)(m-1)(i-+1小.(mi-xn)=1 -会动几 (1.7) 作其组合 Ln()=∑4()fc) (1.8) =0