
二、平均值的置信区间 4→总体平均值 x→有限次测量均值 (I)由单次测量结果估计μ的置信区间 置信限 u=X士u·0 (2)由欢测重的样平均值估计μ的置信区间 ±- (3) 区间 u=x±t,f5x=x±ia/
二、平均值的置信区间 (1)由单次测量结果估计μ的置信区间 (2)由多次测量的样本平均值估计μ的置信区间 (3)由少量测定结果均值估计μ的置信区间 = x u n x u x u x = = n s x t s x t x f x f = = , , → 总体平均值 x → 有限次测量均值 u u x x t s 置信限

例 如何理解μ=47.50%±0.10%置信度P=95%) 解:理解为在47.50%±0.10%的区间内 包括总体均值在内的概率为95% P20表2-3 WHY? 结论:增加置信水平则相应增加置信区间
例 95% 47.50% 0.10% 包括总体均值 在内的概率为 理解为在 的区间内 解: 如何理解 = 47.50% 0.10%(置信度 P = 95% ) P20 表2-3 结论:增加置信水平则相应增加置信区间 WHY?
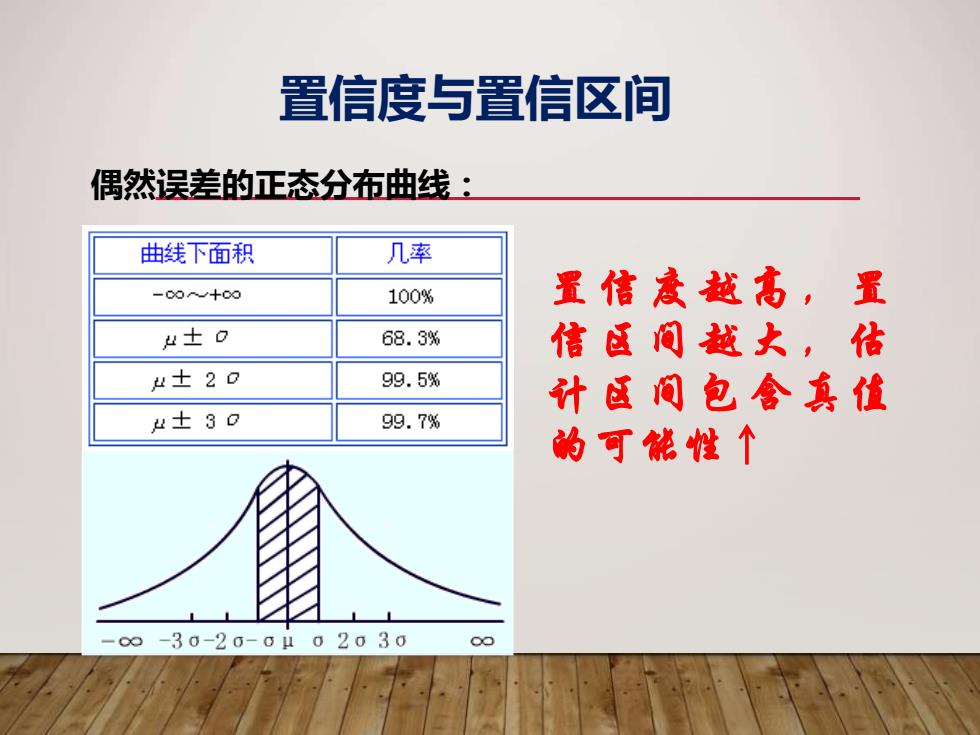
置信度与置信区间 偶然误差的正态分布曲线: 曲线下面积 几率 -00y+00 100% 置信度越高,置 以士O 68.3% 信区同越大,传 4±20 99.5% 计区间包含真值 4±30 99.7% 的可能性个 -∞-30-20-0102030 oo
置信度与置信区间 偶然误差的正态分布曲线: 置信度越高,置 信区间越大,估 计区间包含真值 的可能性↑
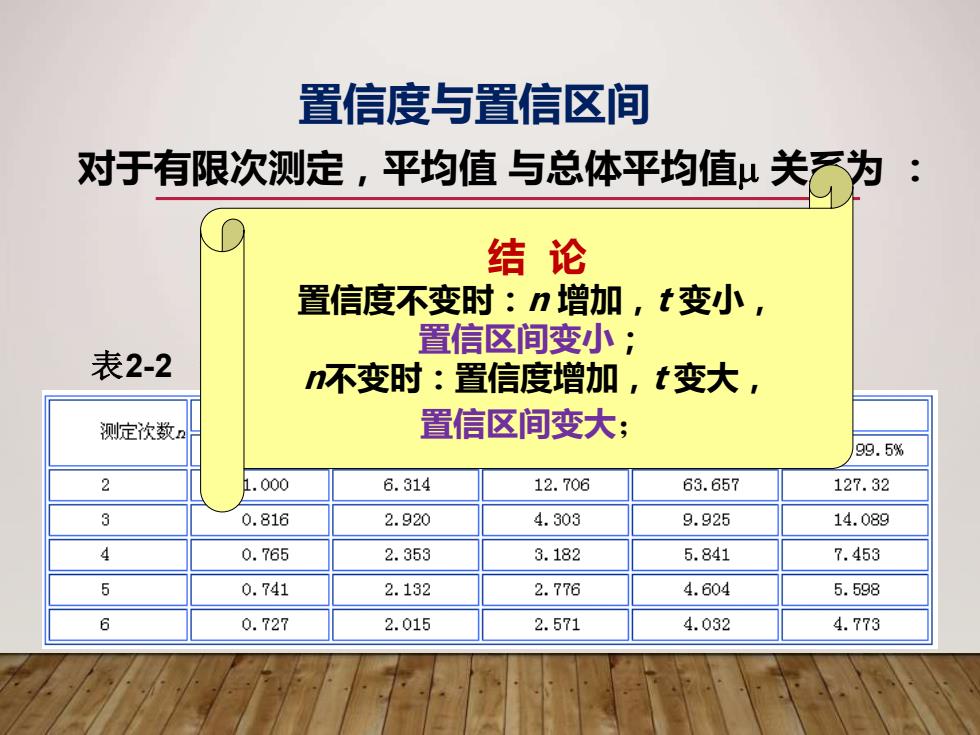
置信度与置信区间 对于有限次测定,平均值与总体平均值μ关为: 结论 置信度不变时:n增加,t变小, 置信区间变小; 表2-2 不变时:置信度增加,t变大, 测定次数。 置信区间变大; 99.5% 2 1.000 6.314 12.706 63.657 127.32 3 0.816 2.920 4.303 9.925 14.089 4 0.765 2.353 3.182 5.841 7.453 5 0.741 2.132 2.776 4.604 5.598 6 0.727 2.015 2.571 4.032 4.773
置信度与置信区间 s.有限次测定的标准偏 差; n.测定次数。 对于有限次测定,平均值 与总体平均值 关系为 : n s = X t 表2-2 t 值表 (注意t值的变化规律) 结 论 置信度不变时:n 增加,t 变小, 置信区间变小; n不变时:置信度增加,t 变大, 置信区间变大;

置信区间 少量测定结果均值估计μ的置信区间 =x±ta,fSx=xta, 其中 S. x+ta.s' 为置信区间的上限→XU Nn X-tas' 为置信区间的下限一→X n
n s x t s x t x f x f = = , , n s x t x f − , n s x t x f + , 少量测定结果均值估计μ的置信区间 其中 为置信区间的上限 为置信区间的下限 XU XL 置信区间