(里度本2*大身 第7章波动学基础 大号物理A教素 波动(2) 主要内容: ⊙波的能量声波
第7章 波动学基础 大学物理A教案 波动(2) 主要内容: 波的能量 声波

国廉本上黄大皇 第7章波动学基础 大学物理A放素 §7.3波的能量声波 1、波的能量 以纵波在棒中传播为例,推导波动传播时,媒质中任一 体元的能量。 6 x>△xk 设棒的截面为S,密度为p。在x处取体元,原长为△x, 体元的质量△m=p△V=pS△x 设棒中纵波的波动表达式为y=AcoS0(亿-) 则体元的振动速度为 0= y=-Awsin@(t-2)
第7章 波动学基础 大学物理A教案 §7 3 波的能量 声波 1、波的能量 §7.3 波的能量 声波 以纵波在棒中传播为例, 推导波动传播时, 媒质中任一 体元的能量。 x o x x 设棒的截面为S ,密度为 。在 x 处取体元, 原长为 , x 体元的质量 m V Sx cos ( ) x 设棒中纵波的波动表达式为 y A t 体元的质量 m V Sx ( ) u y 则体元的振动速度为 i ( ) x A t y sin ( ) u A t t y v
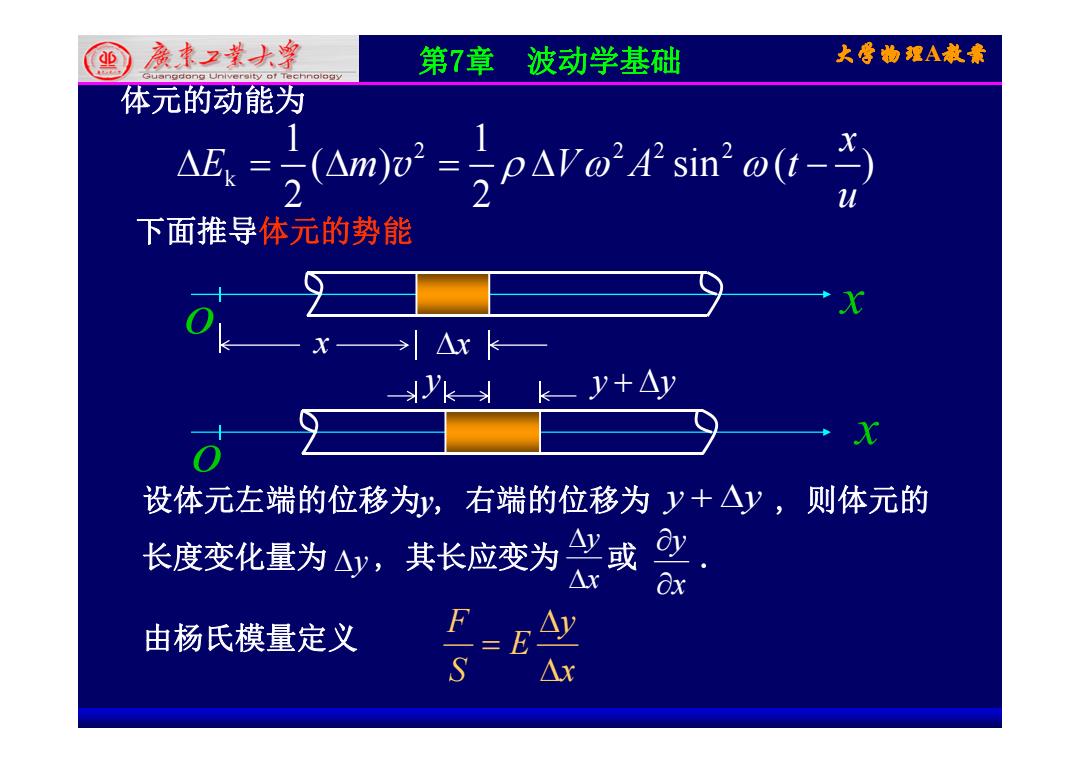
(亲本2素大等 第7章波动学基础 大雪物理A教章 体元的动能为 正.=2wmo-2paro4snou- 下面推导体元的势能 △x k ky+△ 设体元左端的位移为,右端的位移为y+△y,则体元的 长度变化量为△y,其长应变为巴或型 △x Ox 由杨氏模量定义 F-EAY △x
第7章 波动学基础 大学物理A教案 体元的动能为 2 22 2 k 1 1 ( ) sin ( ) 2 2 x E m VA t u v 下面推导体元的势能 x o x x y y y x o y y y o 设体元左端的位移为y, 右端的位移为 , 则体元的 长度变化量为 其长应变为 或 y y y y 长度变化量为 y , 其长应变为 或 . x xy 由杨氏模量定义 y E F S x
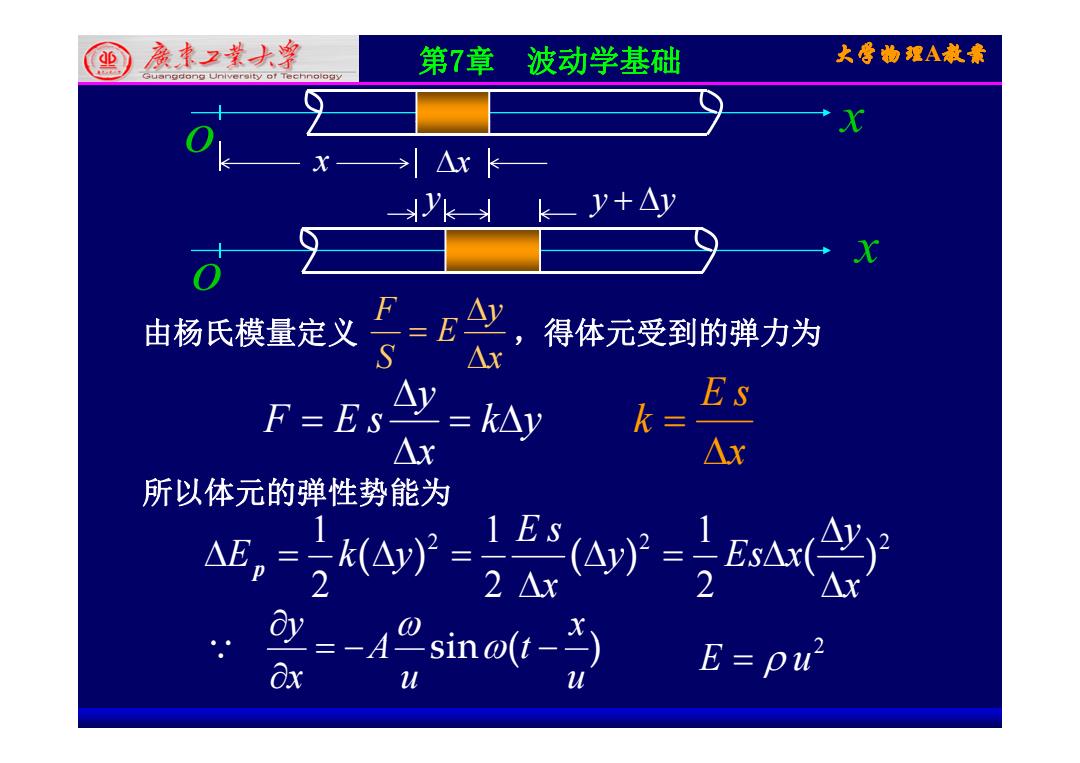
四)度本2菜大穿 第7章 波动学基础 大学物理A教素 >△x yk■ y+△y 由杨氏模量定义=E F ,得体元受到的弹力为 S△x F=EsAY=KAy Es k=兰 △x 所以体元的弹性势能为 () 2△x =-ARsino(t-*) 8x 2 2 E=pu
第7章 波动学基础 大学物理A教案 x o x x y y y x o y y y 由杨氏模量定义 ,得体元受到的弹力为 x y E S F E k y x y F E s x E s k 所以体元的弹性势能为 1 2 1 2 1 2 ( ) ( ) ( ) y y Es x E s E k y 2 2 2 ( ) ( ) ( ) x y Es x x E k y p in ( ) x A t y sin ( ) 2 u t u A x y 2 E u

国桑本2黄大皇 第7章 波动学基础 大学物理A表素 AE=(△m)p2=7p△o2Asin2o- △E,=2 PI AVA(gsin2o- 2PAVO'A'sin'(- 可见,任一时刻体元的动能和势能相等,且相位相同。 体元的总能 △E=△E+△E,=p△Vo2Asin2ot-) 即:体元的总机械能不守恒,随t周期性变化。说明波动中 每一质元都在不断地从前一质元中吸收能量,又不断把能量 传给后一质元。 媒质中所有质元的动能与势能之总和称为波的能量
第7章 波动学基础 大学物理A教案 ( ) ( ) 1 2 1 2 2 2 x 1 x ( ) sin ( ) u x E m V A t 2 2 2 2 21 21 v k 1 2 2 22 ( ) sin ( ) 2 p x E u VA t u u 1 x Ek 1 22 2 sin ( ) 2 x VA t u k 可见, 任 时刻体元的动能和势能相等 一时刻体元的动能和势能相等, 且相位相同。 体元的总能 22 2 i() x E E E VA p sin ( ) E E E VA k t u 即: 体元的总机械能不守恒 体元的总机械能不守恒, 随 t 周期性变化。说明波动中 周期性变化。说明波动中 每一质元都在不断地从前一质元中吸收能量, 又不断把能量 传给后一质元。 媒质中所有质元的动能与势能之总和称为波的能量