
(里度本2*大身 第6章振动学基础 大骨物理A煮兼 第三篇 振动和波动 第6章 振动学基础
第6章 振动学基础 大学物理A教案 第三篇 振动和波动 第6章 振动学基础

国桑水2美大皇 第6章振动学基础 大骨物理A款素 振动(1) 主要内容: 。简谐振动的运动学旋转矢量表示法 。简谐振动的动力学特征 。简谐振动的能量
第6章 振动学基础 大学物理A教案 振动(1) 主要内容: 简谐振动的运动学 旋转矢量表示法 简谐振动的动力学特征 简谐振动的能量

盟廉本2黄大学 第6章振动学基础 大学物理A教兼 §6.1简谐振动的运动学 旋转矢量表示法 振动(vibration) 一个物理量随时间t作周期性变化 5(t)=5(t+T) “周期性”是振动的典型特征 机械振动(mechanical vibration) 物体在一定位置附近作来回往复的运动 1、简谐振动(simple harmonic motion) 定义:一个物理量随时间按正弦或余弦函数的规律变化。 复杂的振动可看成若干简谐振动的合成
第6章 振动学基础 大学物理A教案 §6 1. 简谐振动的运动学 简谐振动的运动学 旋转矢量表示法 旋转矢量表示法 振 动 (vibration) 一个物理量随时间 t 作周期性变化 ( t ) ( t T ) “周期性”是振动的典型特征 机械振动(mechanical vibration) 物体在一定位置附近作来回往复的运动 1、简谐振动(simple harmonic motion) 一个物理量随时间按正弦或余弦函数的规律变化。 复杂的振动可看成若 简谐振动的合成 定义: 复杂的振动可看成若干简谐振动的合成
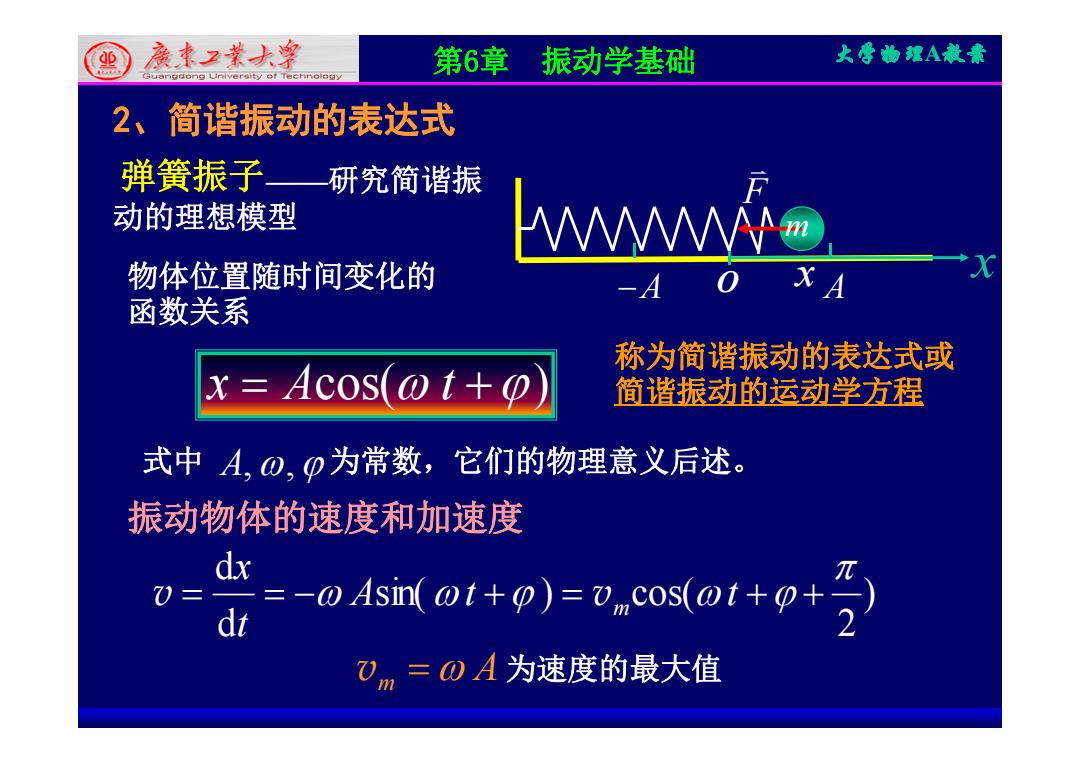
(但亲本2黄大穷 第6章 振动学基础 大骨物理A煮兼 2、简谐振动的表达式 弹簧振子—研究简谐振 动的理想模型 物体位置随时间变化的 函数关系 A 称为简谐振动的表达式或 x Acos(@t+o 简谐振动的运动学方程 式中A,0,0为常数,它们的物理意义后述。 振动物体的速度和加速度 dx 0= =-Asin(@t+o)=vcos(@t++ dt )m=OA为速度的最大值
第6章 振动学基础 大学物理A教案 2、简谐振动的表达式 弹簧振子——研究简谐振 动的理想模型 F 物体位置随时间变化的 O x x A A m x Acos( t ) 函数关系 称为简谐振动的表达式或 简谐振动的运动学方程 A A x Acos( t ) 简谐振动的运动学方程 式中 A,, 为常数,它们的物理意义后述。 振动物体的速度和加速度 d ) 2 sin( ) cos( dd A t t tx m v v vm A 为速度的最大值

第6章 振动学基础 M网 x Acos(@t+p) -A dv a= =-0Ac0s(0t+p)=amc0s(0t+p±π)=-0x dt 4m=0A为加速度的最大值 即:物体作谐振动时,它的位移,速度和加速度都随时间作周 期性变化。 3、简谐振动的特征量 (1)振幅 物体离开平衡位置的最大位移的绝对值。 位移振幅用A表示,速度振幅为Vm,加速度为am
第6章 振动学基础 大学物理A教案 F x Acos( t ) O x x A A m A t a t x t a m 2 2 cos( ) cos( ) dd v A A dt am A 为加速度的最大值 2 即:物体作谐振动时,它的位移,速度和加速度都随时间作周 期性变化。 (1)振幅 3、简谐振动的特征量 、简谐振动的特征量 (1)振幅 物体离开平衡位置的最大位移的绝对值。 位移振幅用 A 表示,速度振幅为 ,加速度为 vm am