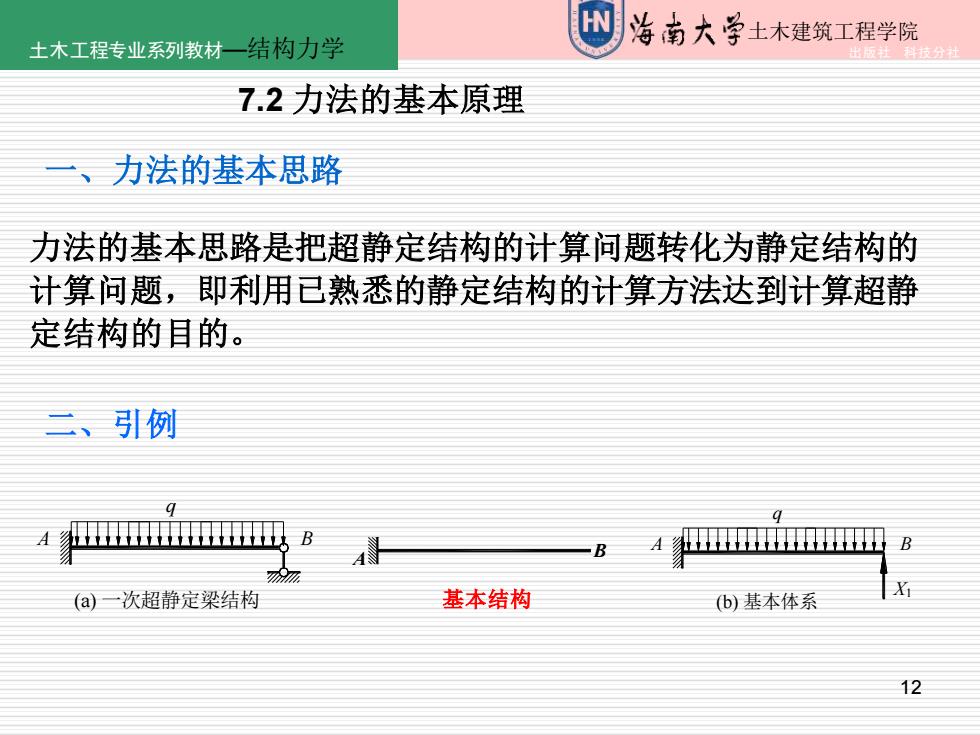
土木工程专业系列教材一结构力学 海南大学土木建筑工程学院 7.2力法的基本原理 、力法的基本思路 力法的基本思路是把超静定结构的计算问题转化为静定结构的 计算问题,即利用已熟悉的静定结构的计算方法达到计算超静 定结构的目的。 三、引例 q 9 A 围 B (a)一次超静定梁结构 基本结构 (b)基本体系 12
12 结构力学—第七章 力法 土木建筑工程学院 7.2 力法的基本原理 一、力法的基本思路 力法的基本思路是把超静定结构的计算问题转化为静定结构的 计算问题,即利用已熟悉的静定结构的计算方法达到计算超静 定结构的目的。 二、引例 q A B (a) 一次超静定梁结构 (b) 基本体系 A q B X1 A B 基本结构 q A B (a) 一次超静定梁结构 (b) 基本体系 A q B X1 土木工程专业系列教材—结构力学 出版社 科技分社

结构力学一第七章力法 治南大学土木建筑工程学院 三、力法的基本原理 力法是以超静定结构的多余约束力作为基本未知量,再根 据基本体系在多余约束处与原结构位移相同的条件,建立 变形协调方程以求解基本未知量,从而把超静定结构的求 解问题转化为静定结构的分析问题。这就是用力法分析超 静定结构的基本原理和计算方法。 四、力法的三个要素 力法的基本未知量计算超静定结构的关键 力法的基本体系一超静定结构转化为静定结构计算的桥梁 力法的基本方程一变形协调条件 13
13 结构力学—第七章 力法 土木建筑工程学院 力法是以超静定结构的多余约束力作为基本未知量,再根 据基本体系在多余约束处与原结构位移相同的条件,建立 变形协调方程以求解基本未知量,从而把超静定结构的求 解问题转化为静定结构的分析问题。这就是用力法分析超 静定结构的基本原理和计算方法。 三、力法的基本原理 四、力法的三个要素 力法的基本未知量─计算超静定结构的关键 力法的基本体系─超静定结构转化为静定结构计算的桥梁 力法的基本方程─变形协调条件
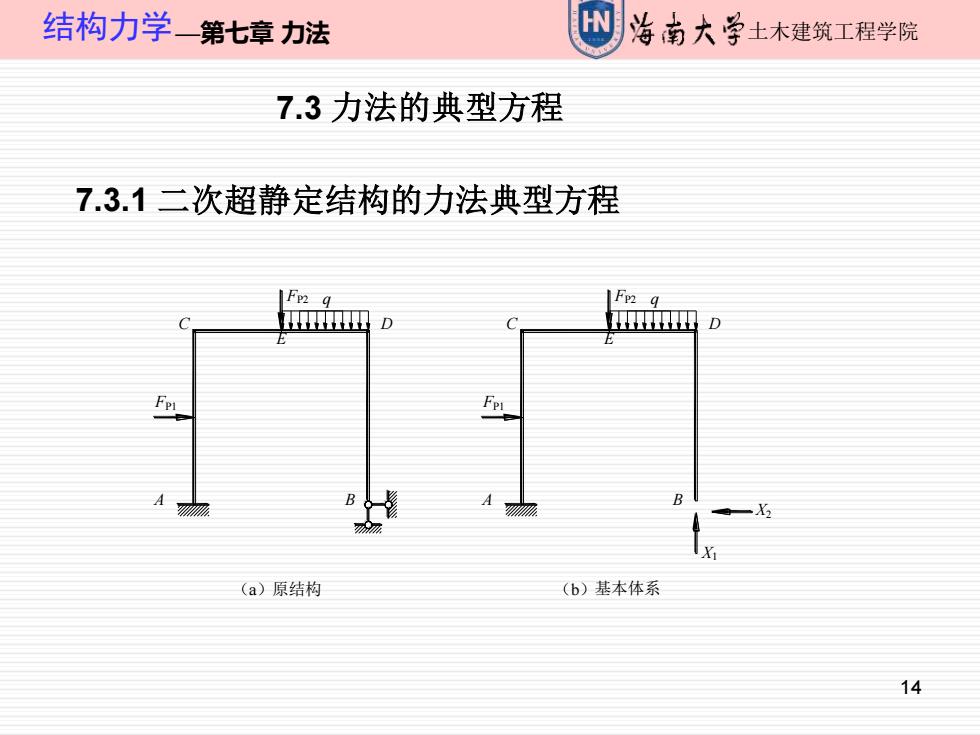
结构力学一第七章力法 W 海南大学土木建筑工程学院 7.3力法的典型方程 7.3.1二次超静定结构的力法典型方程 Fy g D 田D 一X X (a)原结构 (b)基本体系 14
14 结构力学—第七章 力法 土木建筑工程学院 7.3 力法的典型方程 7.3.1 二次超静定结构的力法典型方程 FP1 FP2 q A B C D E (a)原结构 (b)基本体系 A B FP1 C D E FP2 q X1 X2
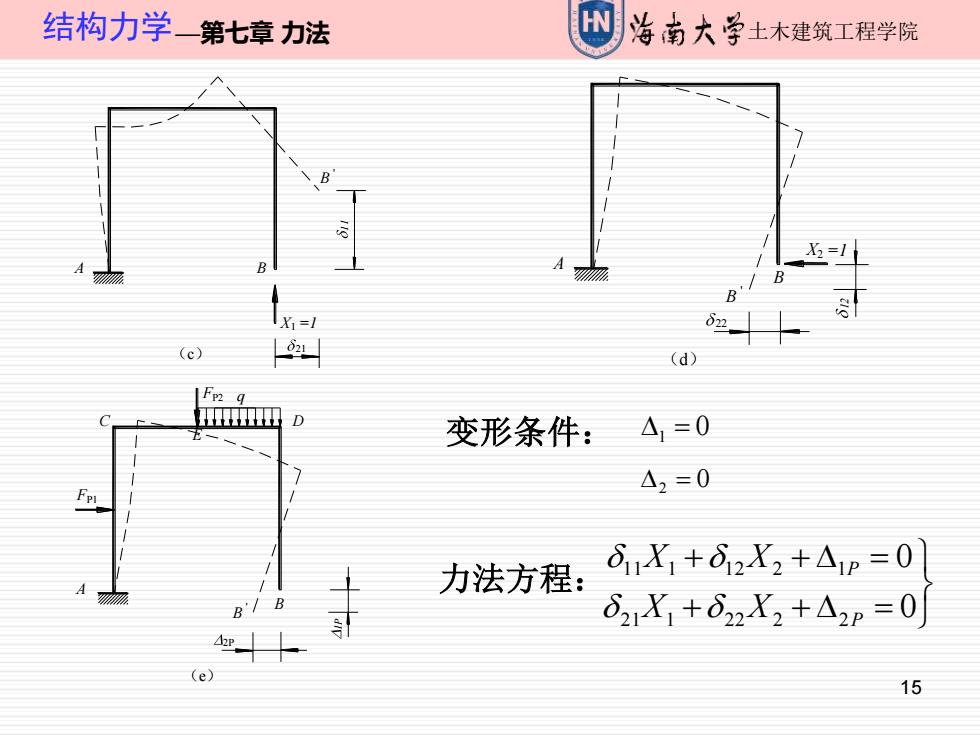
结构力学一第七章力法 治南大学土木建筑工程学院 X=1 B X1=1 (c) (d) 田 D 变形条件: △1=0 △2=0 力法方程: Ci1X1+d2X2+△p=0 B/B δ21X1+O22X2+△2p=0 42P (e) 15
15 结构力学—第七章 力法 土木建筑工程学院 A B X1 (c) 21 11 B ' =1 A B 22 12 X2 (d) B ' =1 FP2 q FP1 E C D A B 2P 1P (e) ' B 变形条件: 0 1 = 2 = 0 + + = + + = 0 0 21 1 22 2 2 11 1 12 2 1 P P X X X X 力法方程:

结构力学一第七章力法 海南大学土木建筑工程学院 7.3.2n次超静定结构的力法典型方程 、典型方程 对于一个n次超静定结构,相应地有n个多余未知力,而每 一个多余未知力处总有一个已知的位移条件相对应,故可按 已知位移条件建立一个含个未知量的代数方程组,从而可 解出个多余未知力。设基本体系上各多余未知力处的位移 为△,i=1,2,n),则此n个方程式为 △1=611X1+612X2+.+61nXn+△1P=0 △2=621X1+622X2+.+62nXm+△2p=0 △n=δnX1+On2X2+.+δmmXn+△nP=0 16
16 结构力学—第七章 力法 土木建筑工程学院 7.3.2 n次超静定结构的力法典型方程 = + + + + = = + + + + = = + + + + = 0 0 0 1 1 2 2 2 2 1 1 2 2 2 2 2 1 1 1 1 1 2 2 1 1 n n n n n n n P n n P n n P X X X X X X X X X 对于一个n次超静定结构,相应地有n个多余未知力,而每 一个多余未知力处总有一个已知的位移条件相对应,故可按 已知位移条件建立一个含n个未知量的代数方程组,从而可 解出n个多余未知力。设基本体系上各多余未知力处的位移 为 i (i =1,2, ,n) ,则此n个方程式为 一、典型方程