
(2)全加器 全加器则是实现两个二进制加数及一个米自低位进位的全加运算。以A、B表示两个 加数,C,表示米自低位的进位,以S和C分别表示全加和及向高位的进位,全加器的真值 表如表2-3所示,由真值表即可得到S和C的逻辑表达式,如(2-2)式和(2-3)式所示. 一位全加器的逻辑图及逻辑符号如图2-4所示。 S.=4B.Cn+4B.C+4.B.Cm+4.B.C =C(dB+AD)+C(4.B,) (2-2) =Cn4.⊕B)+Cn(An田B) =A⊕Bn⊕C C.=4.B.C+4.B.C-+4.B.C+4.B.C (2-3) =Cm-(An⊕Bn)+AnB 表2-3全加器真值表 An Ba Cn-1 Sn Cn Cn Cn Sn 0 0 0 0 0 0 0 0 0 0 FA 0 0 1 0 0 0 0 An Bn Cn-1 An Bn Cn】 1 1 (:)辽辑电路 (6)逐辑特号 3.串行进位并行加法器 图2-4全加器逻辑电路及遂细符号 如果要实现多位二进制数的加法运算,就必须将多个全加器级联。例如将两个全加 器相级联,即构成一个两位二进制加法器,同理一个四位的并行全加器可由上述的四个全加 器级联组成,如图25所示。 Bo Ao Co-u =— C3 S2 1 图2-5四位井行全加器 该电路可将两个加数A、B的各位同时送到相应的全加器的输入端,进位是串行送 数,最低位设置为0。相加数为N位时,应先知道一位全加器的延迟时间TY,那么N位全加 器相级联,征迟时间就是NTY。这种进制信息位加法的运算速度提高很多。使用时可详见 这方面的中规模串行进位、并行加法器的芯片,如T1283,其内部连接方式如图2-6所示
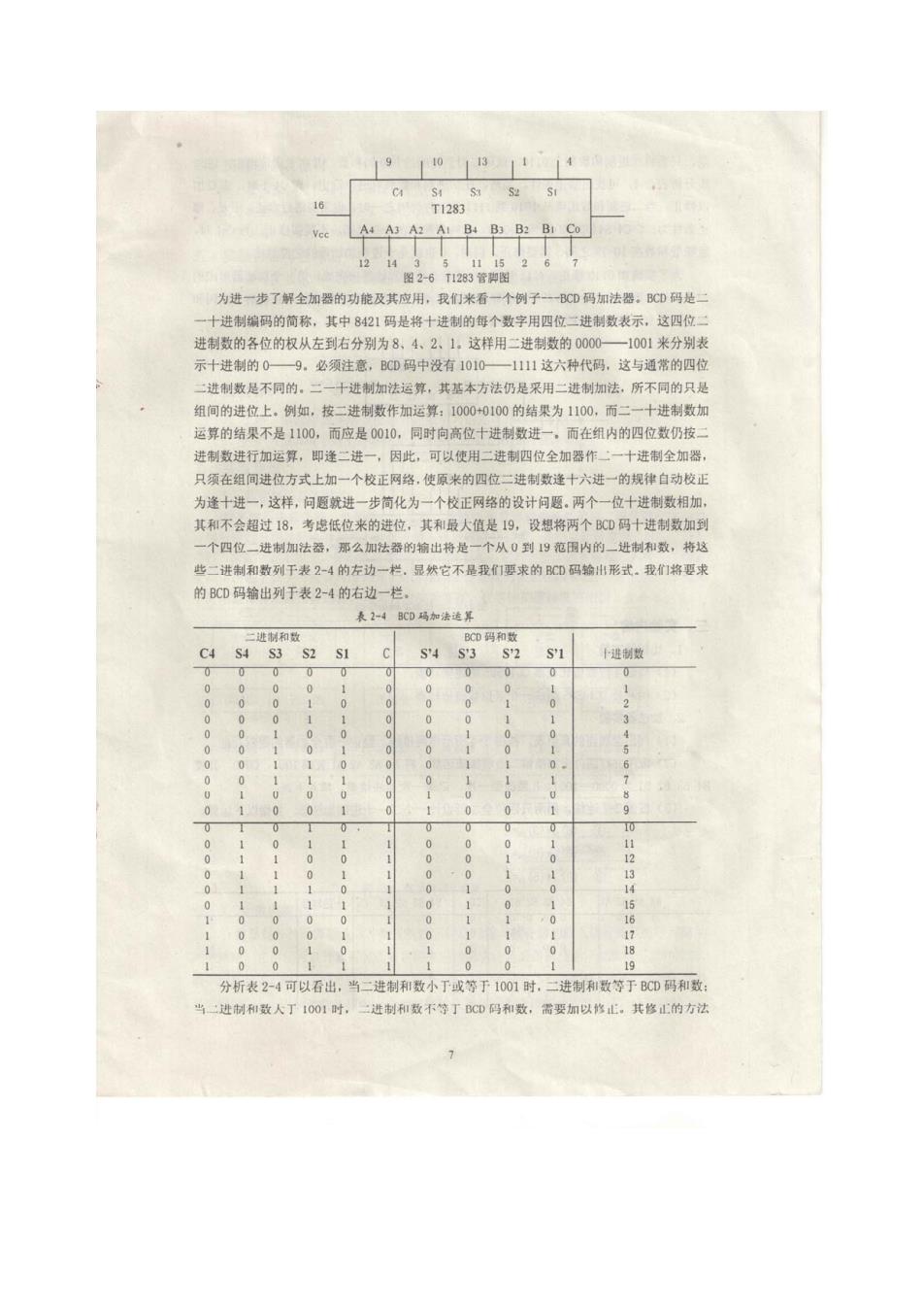
9101311214 S S:S2 SI 16 T1283 A4 A3 A2 A B4 B3 B2 BI Co 12 143 5111526 图2-6T1283管脚图 为进一步了解全加器的功能及其应用,我们米看一个例子一一BCD码加法器。BCD码是 一十进制编码的简称,其中8421码是将十进制的每个数字用四位二进制数表示,这四位 进制数的各位的权从左到右分别为8,4、2、1。这样用二进制数的0000一1001来分别表 示十进制的0一—9。必须注意,BCD码中没有1010一一1111这六种代码,这与通常的四位 二进制数是不同的。二一十进制加法运算,其基本方法仍是采用二进制加法,所不同的只是 组间的进位上,例如,按二进制数作加运算:1000+0100的结果为1100,而二一十进制数加 运算的结果不是1100,而应是0010,同时向高位十进制数进一,而在组内的四位数仍按 进制数进行加运算,即逢二进一,因此,可以使用二进制四位全加器作一一十进制全加器, 只须在组间进位方式上加一个校正网络,使原来的四位二进制数逢十六进一的规律自动校正 为逢十进一,这样,问题就进一步简化为一个校正网络的设计问题,两个一位十进制数相加, 其和不会超过18,考虑低位来的进位,其和最大值是19,设想将两个BCD码十进制数加到 一个四位二进制加法番,那么加法器的输出将是一个从0到19范围内的一进制和数,将这 些二进制和数列干表2-4的左边一栏,显然它不是我1要求的CD码输形式。我们将要求 的BCD码输出列于表2-4的右边一栏. 表2-4CD码加法连算 二进制和数 BCD码和数 C4 S4 S3 S2 SI S4S'3 S2 S1 十进制数 0■ 0 0 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 9 0 0 0 0 0 0 1 0 11 0 0 0 12 0 0 0 14 0 6 0 0 16 0 0 0 0 18 0 0 1 分析表2-4可以看出,当二进制和数小于或等于1001时,二进制和数等于BCD码和数: 当二进制和数人丁1001时,二进制和数不等丁BCD码和数,需要加以修止,其修正的方法