
中国绅我术大空 University of Science and Technology of China 第一章数制和码制 本章目录 >1.1概述 >1.2几种常用的数制 >1.3不同数制间的转换 >1.4二进制算术运算 >1.5几种常用的编码 2017-8-4 第一章数制和码制 §1.1概述 一、数制 定义:多位数码中每一位的构成方法和从低位到高位的进位规则。 二、码制 定义:编制代码时所遵循的规则。 1编码 用文字、符号或者数字表示特定对象的过程。 2代码 具有特定含义的数码,用来表示不同的事物或事物的不同状态。 注:二进制代码的位数(),与需要编码的事物的个数N之间 应满足以下关系: 2"≥N 2017-8-4 第一章数制和码制
2017-8-4 第一章 数制和码制 1 第一章 数制和码制 第一章 数制和码制 本章目录 ¾1.1 概述 ¾1.2 几种常用的数制 ¾1.3 不同数制间的转换 ¾1.4 二进制算术运算 ¾1.5 几种常用的编码 2017-8-4 第一章 数制和码制 2 §1.1 概述 一、数制 定义:多位数码中每一位的构成方法和从低位到高位的进位规则。 2 代码 具有特定含义的数码,用来表示不同的事物或事物的不同状态。 二、码制 定义:编制代码时所遵循的规则。 注:二进制代码的位数(n),与需要编码的事物的个数(N)之间 应满足以下关系: 2n ≥ N 1 编码 用文字、符号或者数字表示特定对象的过程

§1.2几种常用的数制 © ●常用的数制 十进制,二进制,十六进制,八进制 ●数的表示方法 位置记数法、多项式法 2017-8-4 第一章数制和码制 §1.2几种常用的数制 一、十进制 每一位的构成:0,1,2,3,4,5,6,7,8,9 进位规则:逢十进一 任意一个n位整数、m位小数的十进制数可表示为 (D)1o=kn-kn-2…kk1…km =kn-1×10m-+…+k×10°+k1×10-1+…+km×10-m -0 i=-m 推广:任意进制(N进制)数可表示为:(D)w=∑k,N k:第位的系数;N:计数的基数;N:第位的权 2017-8-4 第一章数制和码制
2017-8-4 第一章 数制和码制 3 §1.2 几种常用的数制 z常用的数制 十进制,二进制,十六进制,八进制 z数的表示方法 位置记数法、多项式法 2017-8-4 第一章 数制和码制 4 §1.2 几种常用的数制 一、十进制 每一位的构成:0,1,2,3,4,5,6,7,8,9 进位规则:逢十进一 任意一个n位整数、m位小数的十进制数可表示为 i n i m i m m n n n n m k k k k k D k k k k k 10 10 10 10 10 ( ) . 1 1 1 0 0 1 1 10 1 2 0 1 = × = × + + × + × + + × = ∑ − =− − − − − − − − − − − L L L L k:第i位的系数;N:计数的基数;N :第i位的权 i i 推广:任意进制(N进制)数可表示为: i (D)N = ∑kiN
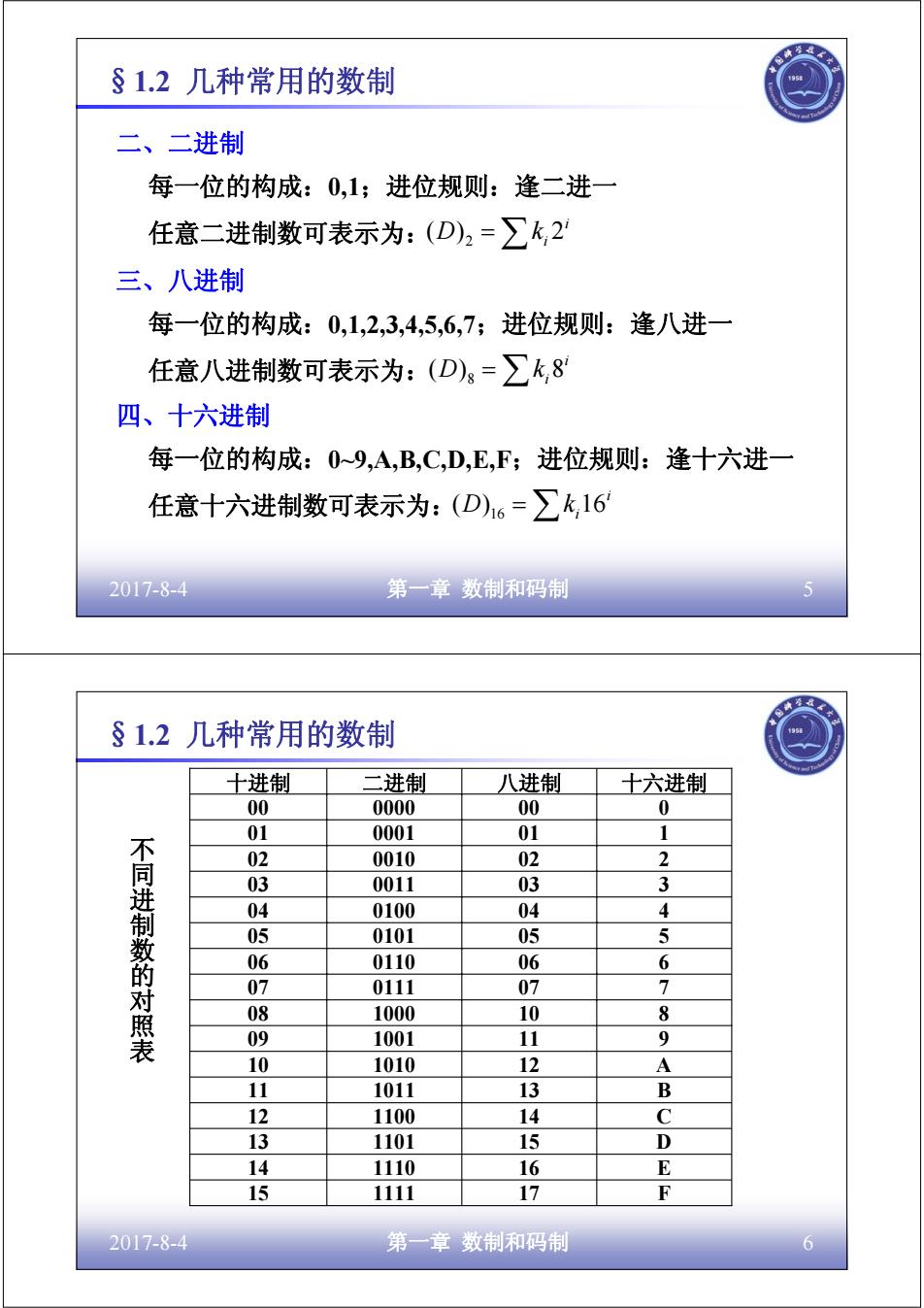
§1.2几种常用的数制 二、二进制 每一位的构成:0,1;进位规则:逢二进一 任意二进制数可表示为:(D)2=∑k,2 三、八进制 每一位的构成:0,1,2,3,4,5,6,7;进位规则:逢八进一 任意八进制数可表示为:(D)g=∑k,8 四、十六进制 每一位的构成:0~9,A,B,C,D,E,F;进位规则:逢十六进一 任意十六进制数可表示为:(D)16=∑k,16 2017-8-4 第一章数制和码制 5 §1.2几种常用的数制 十进制 二进制 八进制 十六进制 00 0000 00 0 01 0001 01 1 02 0010 02 2 不同进制数的对照表 03 0011 03 3 04 0100 04 4 05 0101 05 5 06 0110 06 6 07 0111 07 7 08 1000 10 8 09 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 2017-8-4 第一章数制和码制 6
2017-8-4 第一章 数制和码制 5 §1.2 几种常用的数制 二、二进制 每一位的构成:0,1;进位规则:逢二进一 任意二进制数可表示为: i i (D) k 2 2 = ∑ 三、八进制 每一位的构成:0,1,2,3,4,5,6,7;进位规则:逢八进一 任意八进制数可表示为: i i (D) k 8 8 = ∑ 四、十六进制 每一位的构成:0~9,A,B,C,D,E,F;进位规则:逢十六进一 任意十六进制数可表示为: i i (D) k 16 16 = ∑ 2017-8-4 第一章 数制和码制 6 14 1110 16 E 11 1011 13 B 10 1010 12 A 12 1100 14 C 09 1001 11 9 13 1101 15 D 15 1111 17 F 8 7 6 5 4 3 2 1 0 十六进制 00 0000 00 01 0001 01 03 0011 03 08 1000 10 02 0010 02 07 0111 07 06 0110 06 05 0101 05 04 0100 04 十进制 二进制 八进制 不同进制数的对照表 §1.2 几种常用的数制

§1.3不同数制间的转换 一、任意进制数转换为十进制数 利用公式:(D)N=∑k,N 例:将下面给出的二进制、八进制和十六进制数转换为等值的 十进制数。 (1011.01)2=1×23+0×22+1×2+1×2°+0×21+1×22 =(11.25)10 (32.56)g=3×8+2×8°+5×81+6×8-2 =(26.71875)10 (2A.7F)16=2×16+10×16°+7×16-1+15×16-2 =(42.49609375)10 2017-8-4 第一章数制和码制 §1.3不同数制间的转换 二、十进制数转换为二进制数 一—基数乘除法 整数部分——基数除法 (S)1o=(kkn-1k-2kk)2 (S)0=k,2”+kn-2m+kn-22-2+k2+k20 =2(k2+kn12-2+…+k)+k。 kn2-+kn-12-2+…+k=2(kn2-2+kn-2"-3+…+k2)+k 2017-8-4 第一章数制和码制 8
2017-8-4 第一章 数制和码制 7 = ∑ i (D)N kiN §1.3 不同数制间的转换 2 (1011.01) 8 (32.56) 10 1 0 1 2 (42.49609375) 2 16 10 16 7 16 15 16 = = × + × + × + × − − 一、任意进制数转换为十进制数 例:将下面给出的二进制、八进制和十六进制数转换为等值的 十进制数。 10 3 2 1 0 1 2 (11.25) 1 2 0 2 1 2 1 2 0 2 1 2 = = × + × + × + × + × + × − − 10 1 0 1 2 (26.71875) 3 8 2 8 5 8 6 8 = = × + × + × + × − − 16 (2A.7F) 利用公式: 2017-8-4 第一章 数制和码制 8 0 0 1 1 2 2 1 (S)10 k 2 k 1 2 k 2 k 2 k 2 n n n n n = n + + + + − − − − L 二、十进制数转换为二进制数 2 1 3 1 2 1 2 1 1 k 2 k 2 k 2(k 2 k 2 k ) k n n n n n n n n + + + = + + + + − − − − − − L L ——基数乘除法 整数部分——基数除法 1 0 2 1 1 2(k 2 k 2 k ) k n n n = n + + + + − − − L §1.3 不同数制间的转换 10 1 2 1 0 2 (S) (k k k k k ) = n n− n− L LL

§1.3不同数制间的转换 © 例:(173)10=( )2 2173…余数1(k) 286... 余数0(k) 243 ··。· 余数1(k2) 221…余数1(k) 210 ·…·余数0(k4) 2 5 余数1(k) 2 2 …·余数0(k6) 1 余数1(k) 0 .(173)10=(10101101)2 2017-8-4 第一章数制和码制 §1.3不同数制间的转换 二、十进制数转换为二进制数 ——基数乘除法 小数部分——基数乘法 (S)10=(0.kk2…km)2 (S)10=k121+k222+…+km2m 2(S)h0=k1+(k221+k32-2+…+km2-m+1) 2(k22+k,2-2+…+km2m)=k2+(k32-++km2m+2) 2017-8-4 第一章数制和码制 10
2017-8-4 第一章 数制和码制 9 例: LL LLLLLLLLLLLLLL ( ) 0 k ( )1 k ( ) 2 k ( ) 3 k ( ) 4 k ( ) 5 k ( ) 6 k ( ) 7 k 余数 余数 余数 余数 余数 余数 余数 余数 10 2 (173) = ( ) 10 2 ∴(173) = (10101101) §1.3 不同数制间的转换 2017-8-4 第一章 数制和码制 10 二、十进制数转换为二进制数 ——基数乘除法 小数部分——基数乘法 m m S k k k − − − − − ( ) = − 2 + 2 + + 2 2 2 1 10 1 L 2( ) ( 2 2 2 ) 2 1 3 1 10 1 2 − + − − − − = − + − + + + m m S k k k L k 2( 2 2 2 ) ( 2 2 ) 1 2 2 3 2 1 3 1 2 − + − − − − − + − − − − − + + + = + + + m m m m k k L k k k L k §1.3 不同数制间的转换 10 1 2 2 ( ) (0. ) m S k k k = − − L − LL