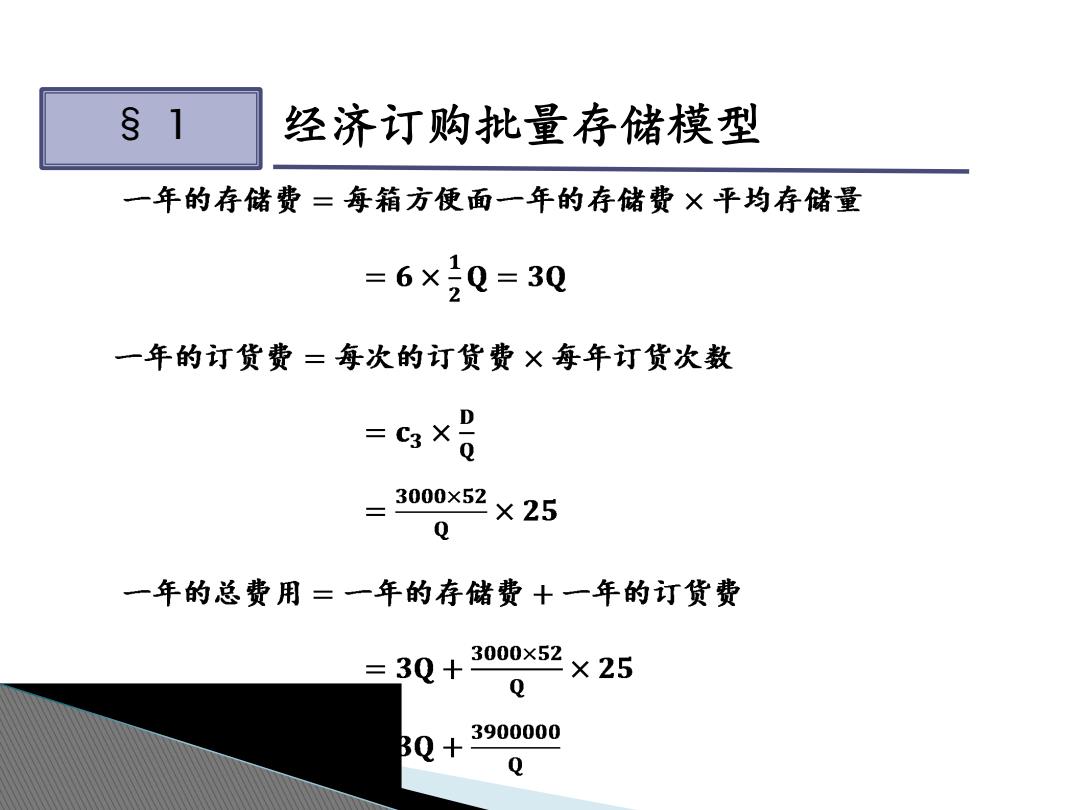
§1 经济订购批量存储模型 一年的存储费=每箱方便面一年的存储费×平均存储量 =6×号Q=3Q 2 一年的订货费=每次的订货费×每年订货次数 -cs D 3000×52 ×25 Q 一年的总费用=一年的存储费十一年的订货费 =3Q+ 3000×52 ×25 3900000 3Q+ Q
§ 1 经济订购批量存储模型

§1 经济订购批量存储模型 最优订货量Q*= 2DC3 2×(3000×52)×25 ≈1140.18 C1 6 365 订货周期T0=3000×52)/1140.18 =2.67(天) 一年的总费用 390000 3900000 TC=3Q*+ Q' 0=3×1140.18+1140.18 =6841.05(元)
§ 1 经济订购批量存储模型

§1 经济订购批量存储模型 灵敏度分析: 最优存储策略是在每次订货费为25元,存储率为20%下 求得的,但是一旦每次订货费或存储率预测值有误差,该存 储策略会有多大变化呢? 管理运筹学软件计算了当存储率和订货费发生变动时,最 优订货量及其最小的一年总费用以及取定订货量为1140.18 箱时一年的总费用
§ 1 经济订购批量存储模型 灵敏度分析: 最优存储策略是在每次订货费为 25 元,存储率为20%下 求得的,但是一旦每次订货费或存储率预测值有误差,该存 储策略会有多大变化呢? 管理运筹学软件计算了当存储率和订货费发生变动时,最 优订货量及其最小的一年总费用以及取定订货量为1140.18 箱时一年的总费用
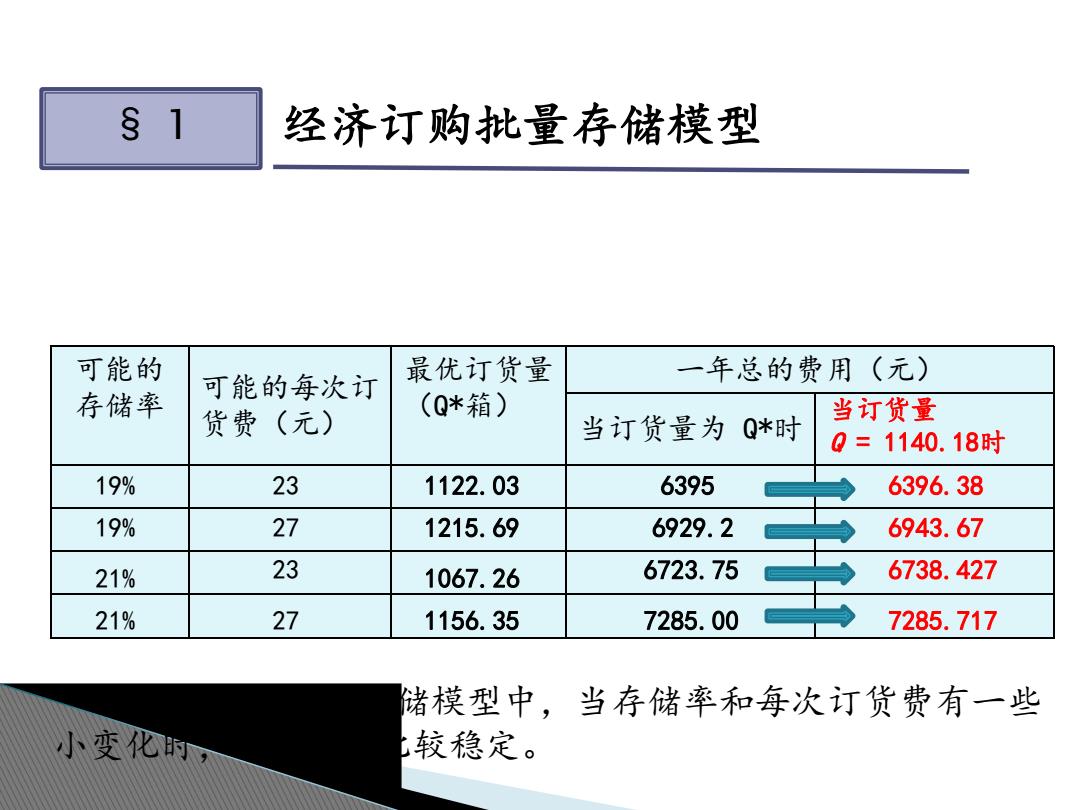
§1 经济订购批量存储模型 可能的 可能的每次订 最优订货量 一年总的费用(元) 存储率 货费(元) (Q*箱) 当订货量为Q*时 当订货量 0=1140.18时 19% 23 1122.03 6395 6396.38 19% 27 1215.69 6929.2 6943.67 21% 23 1067.26 6723.75 6738.427 21% 27 1156.35 7285.00 7285.717 储模型中,当存储率和每次订货费有一些 小变化的, 较稳定
§ 1 经济订购批量存储模型 可能的 存储率 可能的每次订 货费(元) 最优订货量 (Q*箱) 一年总的费用(元) 当订货量为 Q*时 19% 19% 23 27 1122.03 1215.69 21% 21% 23 27 1067.26 1156.35 6395 6396.38 6929.2 6943.67 6723.75 6738.427 7285.00 7285.717 当订货量 Q = 1140.18时 在经济订购批量存储模型中,当存储率和每次订货费有一些 小变化时,最优方案比较稳定

§1 经济订购批量存储模型 在最优方案后,批发部根据具体情况进行了一些修改。 (1)订货周期2.67天不符合工作习惯,把订货周期改为3天, 则订货量为:3×3000×52/365=1282箱。 (2)为防止每周需求超过3000箱,每天多存储200箱, 则第一次订货量为1282+200=1482箱,每隔3天补充1282 箱。 (3)提前一天订货时,订货点为427箱。如果需要提前两天 订货,则再订货点为427×2=854箱
§ 1 经济订购批量存储模型 在最优方案后,批发部根据具体情况进行了一些修改。 (1)订货周期2.67天不符合工作习惯,把订货周期改为3天, 则订货量为:3×3000×52/365=1282 箱。 (2)为防止每周需求超过 3000 箱,每天多存储 200 箱, 则第一次订货量为 1282+200=1482 箱,每隔 3 天补充 1282 箱。 (3)提前一天订货时,订货点为427箱。如果需要提前两天 订货,则再订货点为427×2=854 箱