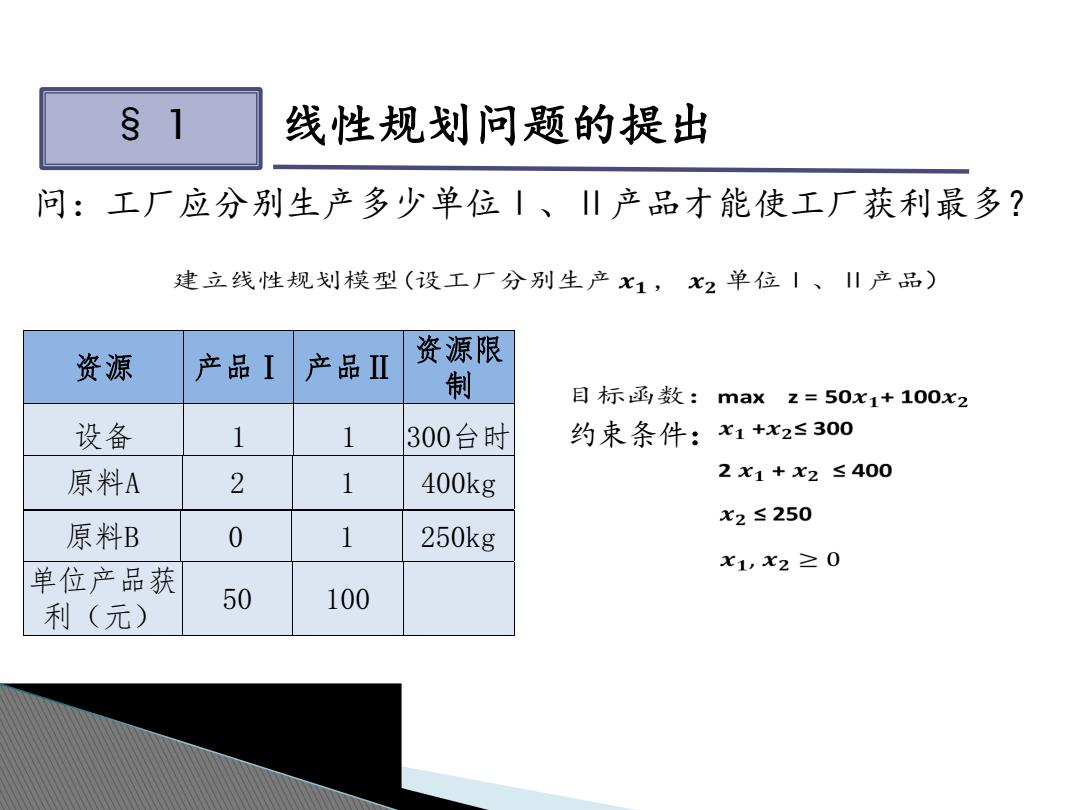
§1 线性规划问题的提出 问:工厂应分别生产多少单位1、川产品才能使工厂获利最多? 建立线性规划模型(设工厂分别生产x1,x2单位丨、川产品) 资源 产品I 产品Ⅱ 资源限 制 目标函数:maxz=50x1+100x2 设备 1 1 300台时 约束条件:x1+x2≤300 原料A 2 1 400kg 2x1+x2≤400 x2≤250 原料B 0 1 250kg x1,x2≥0 单位产品获 利(元) 50 100
§ 1 线性规划问题的提出 问:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多? 约束条件: 资源 产品Ⅰ 产品Ⅱ 资源限 制 设备 1 1 300台时 原料A 2 1 400kg 原料B 0 1 250kg 单位产品获 利(元) 50 100
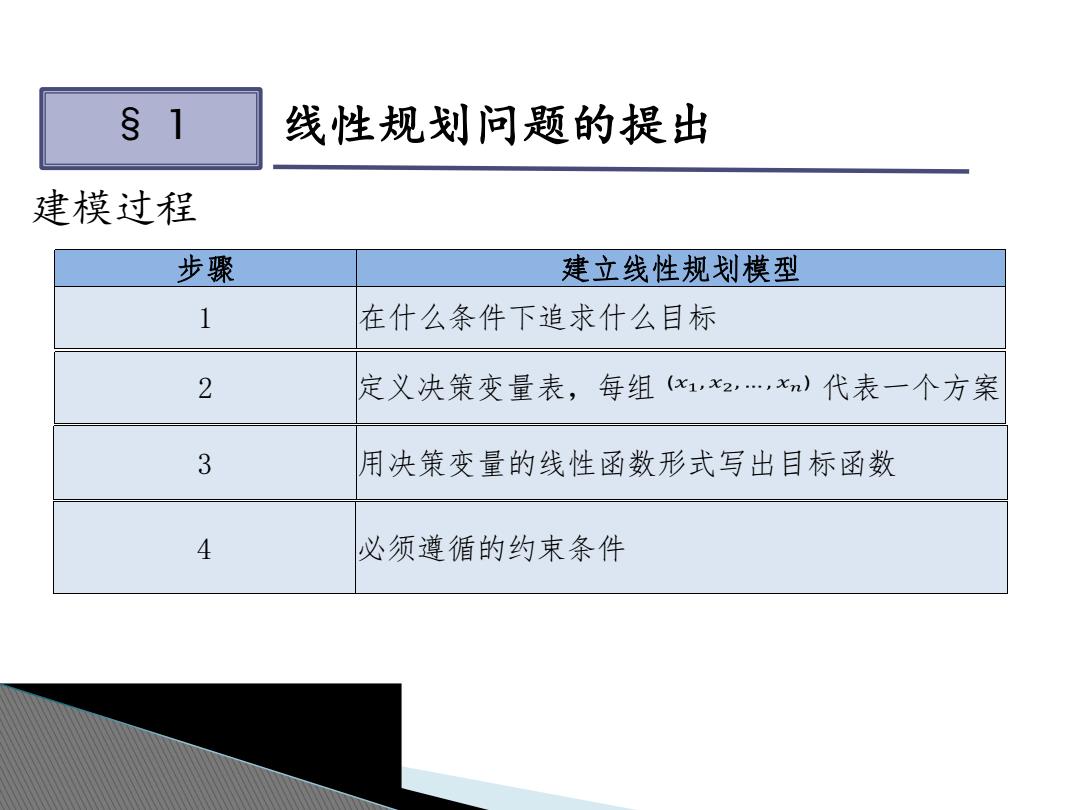
§1 线性规划问题的提出 建模过程 步骤 建立线性规划模型 1 在什么条件下追求什么目标 2 定义决策变量表,每组(x1,x2,xn)代表一个方案 3 用决策变量的线性函数形式写出目标函数 4 必须遵循的约束条件
§ 1 线性规划问题的提出 建模过程 步骤 建立线性规划模型 1 在什么条件下追求什么目标 2 定义决策变量表,每组 代表一个方案 3 用决策变量的线性函数形式写出目标函数 4 必须遵循的约束条件

§1 线性规划问题的提出 模型一般形式 目标函数:max(min)z=c1x1+c2x2+.+cnxn 约束条件: a11x1+a12x2+..+a1nxn≤(=,≥)b1 a21x1+a22x2+..+a2nxn≤(=,≥)b2 ””…”… am1x1+am2x2+..+amn Xn≤(=,≥)bm x1,2,…,xn≥0
§ 1 线性规划问题的提出

本章内容 问题的提出 图解法 图解法的灵敏度分析
问题的提出 图解法 图解法的灵敏度分析 本章内容 1 2 3

§2 图解法 两个决策变量的线性问题,可以用图解法求解。 例1 目标函数: maxz=50x1+100x2 约束条件:X1+X2≤300 2X1+X2 ≤400 x2≤250 X1,X2≥0
§ 2 图解法 两个决策变量的线性问题,可以用图解法求解