
山东理工大客不确定在宏观领域中不显示作用:SHANDONGUNIVERSITYOFTECHNOLOGY举例:一质量为0.001的足够小的粒子,以1m.s-1的速度作直线运动,若速度的不确定度为百万分之一(10-6),则坐标的不确定度:6.6×10-34hh-6 ~ 6.6×10-22 mAx~mA10~×1×10-6AP强宏观物体其动量和位置可同时确定对于电子,在上述相同情况下:6.6 ×10-34Ax =9.1x10-31x1x10-~ 730 m远远超过原子中电子离核的距离,微观粒子其动量和位置不能同时确定。即微观粒子没有确定的运动轨迹
12 不确定在宏观领域中不显示作用: 举例:一质量为0.001g的足够小的粒子,以1m•s -1的速度作直线运动, 若速度的不确定度为百万分之一(10-6),则坐标的不确定度: 34 22 6 6 6.6 10 6.6 10 10 1 10 x h h x m P m − − − − = = 对于电子,在上述相同情况下: 34 31 6 6.6 10 730 9.1 10 1 10 x m − − − = 宏观物体其动量和位置可同时确定 远远超过原子中电子离核的距离,微观粒子其动量和位置 不能同时确定。即微观粒子没有确定的运动轨迹
山东理工大客$8.1量子力学基本假设SHANDONGUNIVERSITYOFTECHNOLOGY1.粒子运动的经典力学描述运动方程的积分:mdcFp = Ft + P.mdtFPot2+t+&.α三2mm运动方程:结论:(1)做一维运动的粒子d"cFm二其运动状态由其坐标和动量dt?完全确定。c, Pr
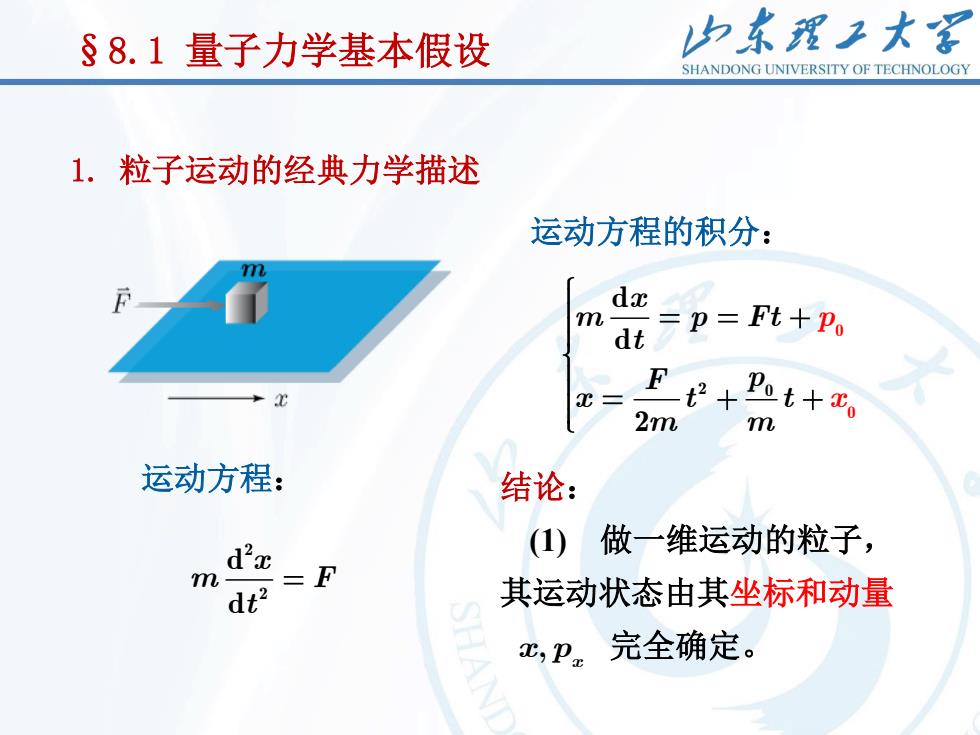
13 §8.1 量子力学基本假设 运动方程: 2 2 d d x m F t 运动方程的积分: 2 0 0 0 d d 2 x m p Ft t F p x t t m p x m 结论: (1) 做一维运动的粒子, 其运动状态由其坐标和动量 x p, x 完全确定。 1. 粒子运动的经典力学描述

山东理工大客SHANDONGUNIVERSITYOFTECHNOLOGY推广至含有N个粒子的系统,系统状态的确定需要指定每个粒子的坐标α,,y,,z及动量Pia,Piu,Piz,即由 N个宏观粒子组成的系统的状态需要2×3N个变量确定。(2)系统的状态随时间的变化由牛顿第二定律确定。(3)系统的物理量表示为粒子的坐标和动量的函数。例如,处于重力场或电磁场中运动的粒子的能量:E = V(c,y,z) + 1m217,221= V(c,y,z) +p+p+p2m式中,V(α,y,z)为粒子在重力场或电磁场中的势能
14 (2) 系统的状态随时间的变化由牛顿第二定律确定。 推广至含有 个粒子的系统,系统状态的确定需要指定 每个粒子的坐标 及动量 ,即由 个 宏观粒子组成的系统的状态需要 个变量确定。 , , i i i x y z , , , , , i x i y i z p p p 2 3N N N (3) 系统的物理量表示为粒子的坐标和动量的函数。 例如,处于重力场或电磁场中运动的粒子的能量: 2 2 2 2 2 2 1 ( , , ) 2 1 ( , , ) 2 x y z x y z E V x y z m v v v V x y z p p p m 式中,V x y z ( , , )为粒子在重力场或电磁场中的势能
山东理工大客SHANDONGUNIVERSITYOFTECHNOLOGY再如,绕定点运动粒子的角动量L:L=πxP1L=rxp= (yp-zp,) +(zp acp) +(cpyp,)k式中,i,和分别为 ,和 方向上的单位矢量
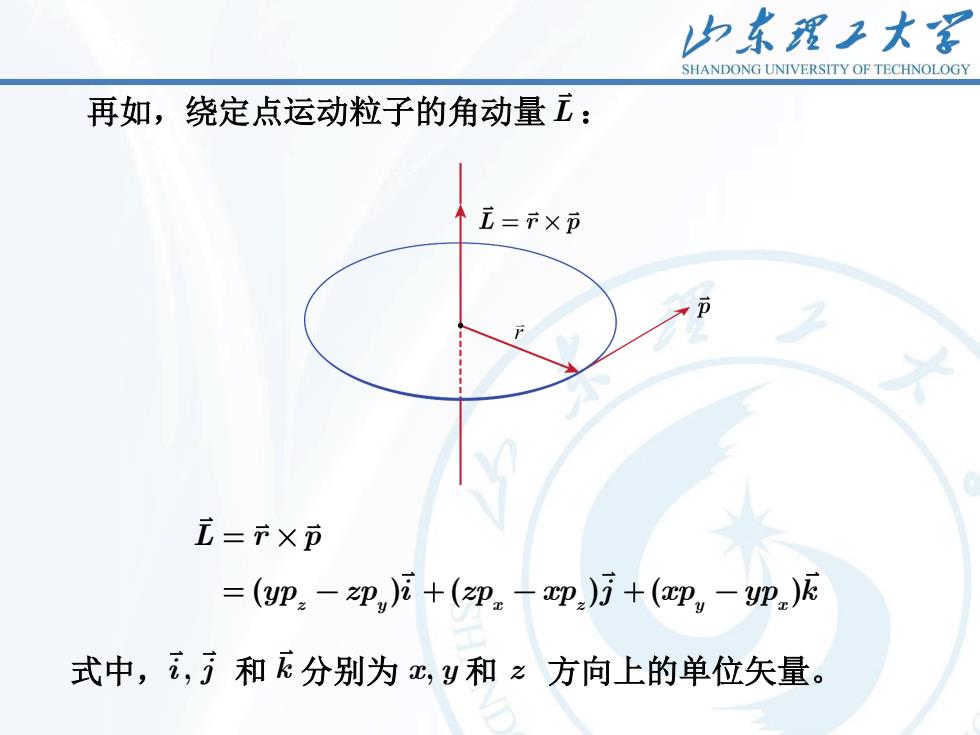
15 再如,绕定点运动粒子的角动量 L : ( ) ( ) ( ) z y x z y x L r p yp zp i zp xp j xp yp k 式中,i j , 和 k 分别为 x y, 和 z 方向上的单位矢量

山东理工大客2.微观粒子系统SHANDONGUNIVERSITYOFTECHNOLOGY对微观粒子系统,由于粒子的坐标和与之对应的动量不能同时精确测量,因此不能像宏观系统一样通过指定每个粒子的坐标和动量来确定系统的状态,故做以下假定。招7假定一:由 N个粒子组成的微观系统,其状态可由这N个粒子的坐标的函数亚(t,q,qz,…)[或动量的函数亚(t,P,P,,…)]描述亚(t,q,,,,)称为波函数*为了叙述上的方便,常将坐标写做9,如对于一个单粒子系统,其坐标为 α,y,z,写做q,q2,q
16 2. 微观粒子系统 对微观粒子系统,由于粒子的坐标和与之对应的动量不 能同时精确测量,因此不能像宏观系统一样通过指定每个 粒子的坐标和动量来确定系统的状态,故做以下假定。 假定一 : 由 个粒子组成的微观系统,其状态可由这 个粒 子的坐标的函数 [或动量的函数 ] 描述 称为波函数。 1 2 ( , , , ) t q q 1 2 ( , , , ) t p p 1 2 ( , , , ) t q q N N *为了叙述上的方便,常将坐标写做 q,如对于一个单粒 子系统,其坐标为 x y z , , ,写做 q q q 1 2 3 , ,