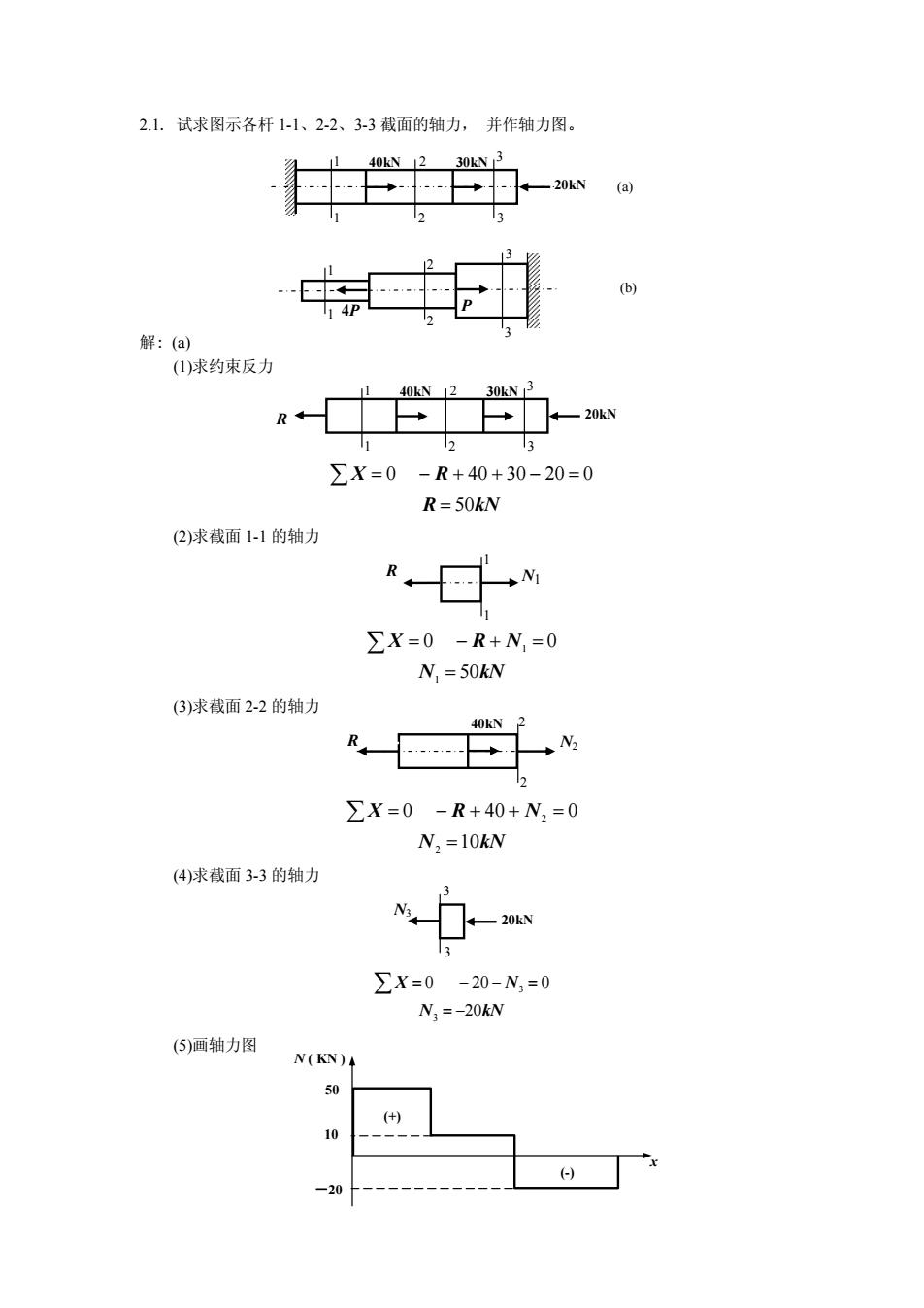
2.1.试求图示各杆1-1、2-2、3-3截面的轴力,并作轴力图。-.-.解: (a)(1)求约束反力OKNKNIZX=0-R+40+3020=0R=50kN(2)求截面 1-1 的轴力ZX=0 -R+N,=0N,=50kN(3)求截面2-2的轴力OkNZX=0-R+40+N,=0N, =10kN(4)求截面 3-3的轴力Zx=0N,=-20KN(5)画轴力图N(KN)50
2.1. 试求图示各杆 1-1、2-2、3-3 截面的轴力, 并作轴力图。 3 1 1 3 2 40kN 2 20kN 30kN (a) 1 1 2 2 3 3 4P P (b) 解: (a) (1)求约束反力 3 1 1 3 2 40kN 2 20kN 30kN R R kN RX 50 0203040 0 = ∑ = − + + − = (2)求截面 1-1 的轴力 N1 1 1 R kNN NRX 50 0 0 1 1 = ∑ = − + = (3)求截面 2-2 的轴力 40kN 2 2 R N2 kNN NRX 10 040 0 2 2 = ∑ = − + + = (4)求截面 3-3 的轴力 3 3 20kN N3 3 3 0 20 0 20 X N N kN = −− = = − ∑ (5)画轴力图 x -20 10 50 N ( KN ) (+) (-)
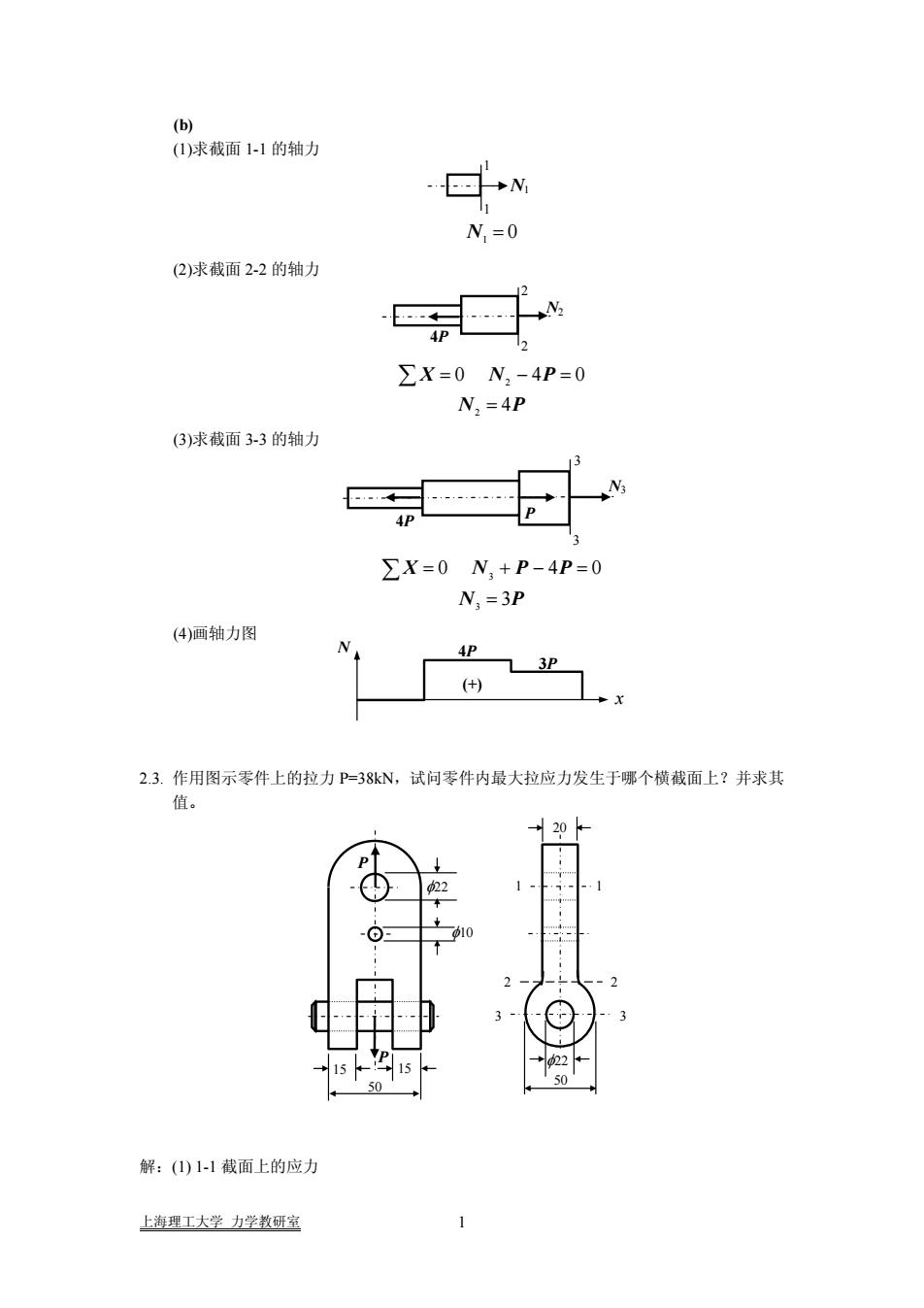
(b) (1)求截面 1-1 的轴力V(2)求截面 2-2 的轴力ZX=0 N,-4P=0N, =4P(3)求截面 3-3 的轴力ZX=0 N,+P-4P=0N, =3P(4)画轴力图(+)2.3.作用图示零件上的拉力P=38kN,试问零件内最大拉应力发生于哪个横截面上?并求其值。解:(1)1-1截面上的应力上海理工大学力学教研室
(b) (1)求截面 1-1 的轴力 1 1 N1 0 N1 = (2)求截面 2-2 的轴力 2 2 N2 4P PN PNX 4 04 0 2 2 = ∑ = − = (3)求截面 3-3 的轴力 N3 3 3 P 4P PN PPNX 3 0 04 3 3 = ∑ = + − = (4)画轴力图 x N (+) 4P 3P 2.3. 作用图示零件上的拉力 P=38kN,试问零件内最大拉应力发生于哪个横截面上?并求其 值。 P P 50 15 15 φ22 φ10 50 φ22 20 2 2 3 3 1 1 解:(1) 1-1 截面上的应力 上海理工大学 力学教研室 1

38×10367.86MPaA(50-22)×20×10-(2)2-2截面上的应力38x103=63.33MPa42×15×20×10-6(3)3-3截面上的应力P38×103=45.24MPa.A(50-22)×15×2×10-(4)最大拉应力在1-1截面上0 mx =0,=67.86MPa2.4.设图示结构的1和2两部分皆为刚体,钢拉杆BC的横截面直径为10mm,试求拉杆内的应力。解:(1)以刚体CAEZm =0 N, ×4.5+N.×1.5-P×3=0(2)以刚体 BDE为研究对象Zm,=0N,x1.5-N,×0.75=0上海理工大学力学教研室
1 6 1 3 38 10 67.86 (50 22) 20 10 P MPa A σ − × = = = − ×× (2) 2-2 截面上的应力 3 2 6 2 38 10 63.33 2 15 20 10 P MPa A σ − × = = = ×× × (3) 3-3 截面上的应力 3 3 6 3 38 10 45.24 (50 22) 15 2 10 P MPa A σ − × = = = − × ×× (4) 最大拉应力在 1-1 截面上 86.67 MPa max =σσ 1 = 2.4. 设图示结构的 1 和 2 两部分皆为刚体,钢拉杆 BC 的横截面直径为 10mm,试求拉杆内 的应力。 D C B A P=7.5kN G E 3m 0.75m 1.5m 1.5m 1.5m 1 2 解:(1) 以刚体 CAE 为研究对象 NC NE’ G E C A 3m 1.5m P=7.5kN 1.5m ∑ = × + × − × = 035.15.4 0 ' A Nm E C PN (2) 以刚体 BDE 为研究对象 ∑ = × − × = 075.05.1 0 D E NNm B NE D B E 0.75m NB 1.5m 上海理工大学 力学教研室 2
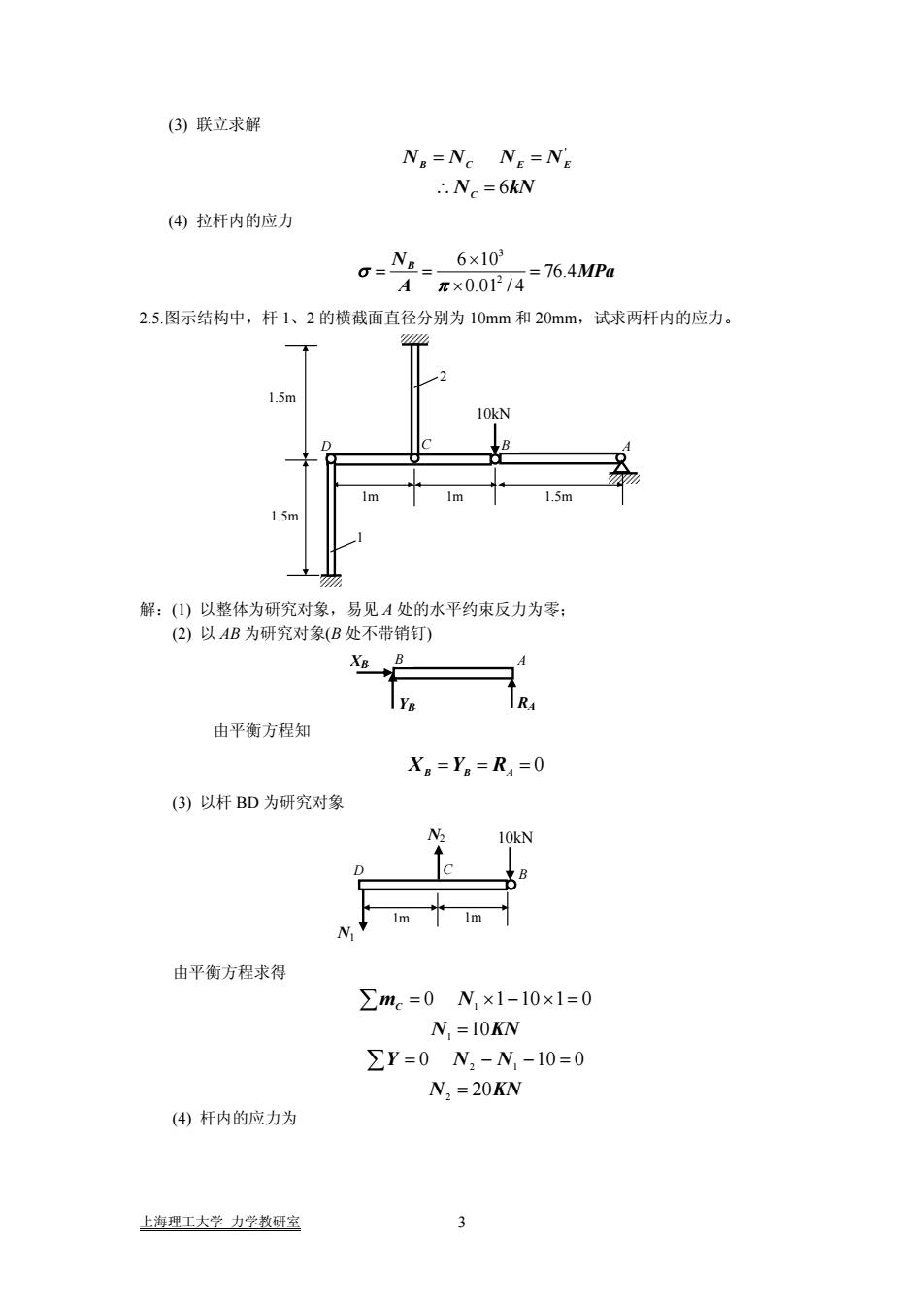
(3)联立求解N.=N. N,=Ne.N=6kN(4)拉杆内的应力6×103NR76.4MPa元×0.01/4A2.5.图示结构中,杆1、2的横截面直径分别为10mm和20mm,试求两杆内的应力。解:(1)以整体为研究对象,易见A处的水平约束反力为零;(2)以AB为研究对象(B处不带销钉)专IYe由平衡方程知X,=Y,=R, =0(3)以杆 BD 为研究对象OkM由平衡方程求得Zmc=0N,×1-10×1=0N, =10KNZY=0 N,-N,-10-0N, =20KN(4)杆内的应力为上海理工大学力学教研室
(3) 联立求解 kNN NNNN C B C E E 6 ' =∴ = = (4) 拉杆内的应力 3 2 6 10 76.4 0.01 / 4 NB MPa A σ π × == = × 2.5.图示结构中,杆 1、2 的横截面直径分别为 10mm 和 20mm,试求两杆内的应力。 解:(1) 以整体为研究对象,易见 A 处的水平约束反力为零; (2) 以 AB 为研究对象(B 处不带销钉) 由平衡方程知 = = = 0 RYX ABB (3) 以杆 BD 为研究对象 由平衡方程求得 KNN NNY KNN C Nm 20 0 010 10 01101 0 2 12 1 1 = =−−= = = × − × = ∑ ∑ (4) 杆内的应力为 B N2 N1 1m 1m D C 10kN XBB B A YBB RA 2 1 B A 1m 1m D C 10kN 1.5m 1.5m 1.5m 上海理工大学 力学教研室 3
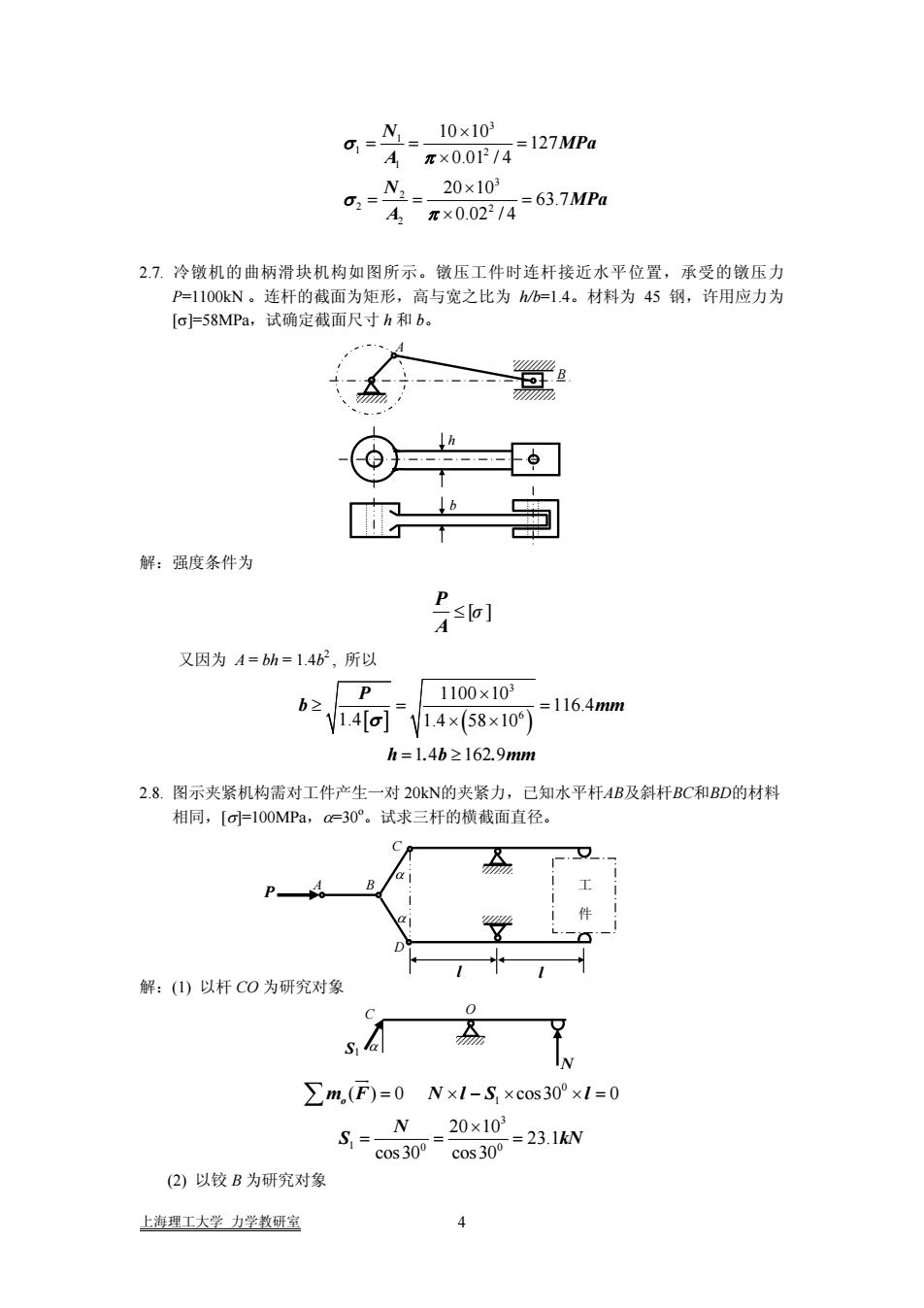
10×10127MPa元×0.01/4A-N_20x10=63.7MPa6元×0.022/42.7.冷镦机的曲柄滑块机构如图所示。镦压工件时连杆接近水平位置,承受的镦压力P=1100kN。连杆的截面为矩形,高与宽之比为h/b=1.4。材料为45钢,许用应力为[o]=58MPa,试确定截面尺寸h和b0解:强度条件为Ss0l又因为A=bh=1.4b,所以b2P1100×103116.4mm1.4[0]1.4×(58×10]h=1.4b≥162.9mm2.8.图示夹紧机构需对工件产生一对20kN的夹紧力,已知水平杆AB及斜杆BC和BD的材料相同,[o]=100MPa,α=30°。试求三杆的横截面直径。解:(1)以杆CO为研究对象S,Zm,(F)=0 N×1-S,×cos30°xl=020×103= 23.1kNS.cOs30°COS300(2)以铰B为研究对象4上海理工大学力学教研室
3 1 1 2 1 3 2 2 2 2 10 10 127 0.01 / 4 20 10 63.7 0.02 / 4 N MPa A N MPa A σ π σ π × == = × × == = × 2.7. 冷镦机的曲柄滑块机构如图所示。镦压工件时连杆接近水平位置,承受的镦压力 P=1100kN 。连杆的截面为矩形,高与宽之比为 h/b=1.4。材料为 45 钢,许用应力为 [σ]=58MPa,试确定截面尺寸 h 和 b。 :强度条件为 A B b h 解 ≤ σ ][ A P 又因为 A = bh = 1.4b2 , 所以 [ ] ( ) 3 6 1100 10 116.4 1.4 1.4 58 10 1 4 162 9 P b m h . b . mm σ × ≥= = × × = ≥ m 2.8. 图示夹 20kN的夹紧力,已知水平杆AB及斜杆BC和BD的材料 相同,[σ]=100MPa,α=30o 。试求三杆的横截面直径。 :(1) 以杆 CO 紧机构需对工件产生一对 解 为研究对象 A B P C l l α 工 D 件 α O 0 1 3 1 0 0 ( ) 0 cos30 0 20 10 23.1 cos30 cos30 mF N l S l o N S kN = ×− × ×= × == = ∑ JJG (2) 以铰 B 为研究对象 S1 C N α 上海理工大学 力学教研室 4