13.1.两根圆截面杆材料相同,尺寸如图所示,一根为等截面杆,一根为变截面杆,试比较两杆的变形能。TT[2]31/8IPLP(a)解:方法1:两杆的变形PL4PLP(3L/8),P(L/4) 7PLNlo"EA"ErN(b) =2x*En(2d)/4End’/4"4Ed?外力的功2P°L7P?LWoa- plo-SEaWo--Plo,- Erl功能原理2PL7P2LUea=Wo-ErtUe,=Won=sErt方法2:两杆的内力N(a) =P N(b)=P变形能_N?L_PL_ 2P2LUa=2EA-2E元d/4E元dp2(3L/8)P (L/4)_7P°LU(b) =22E元(2d)/42End/48End13.2.图示杆架各杆的材料相同截面面积相等,在P力作用下,试求桁架的变形能YT解:(I)求约束力
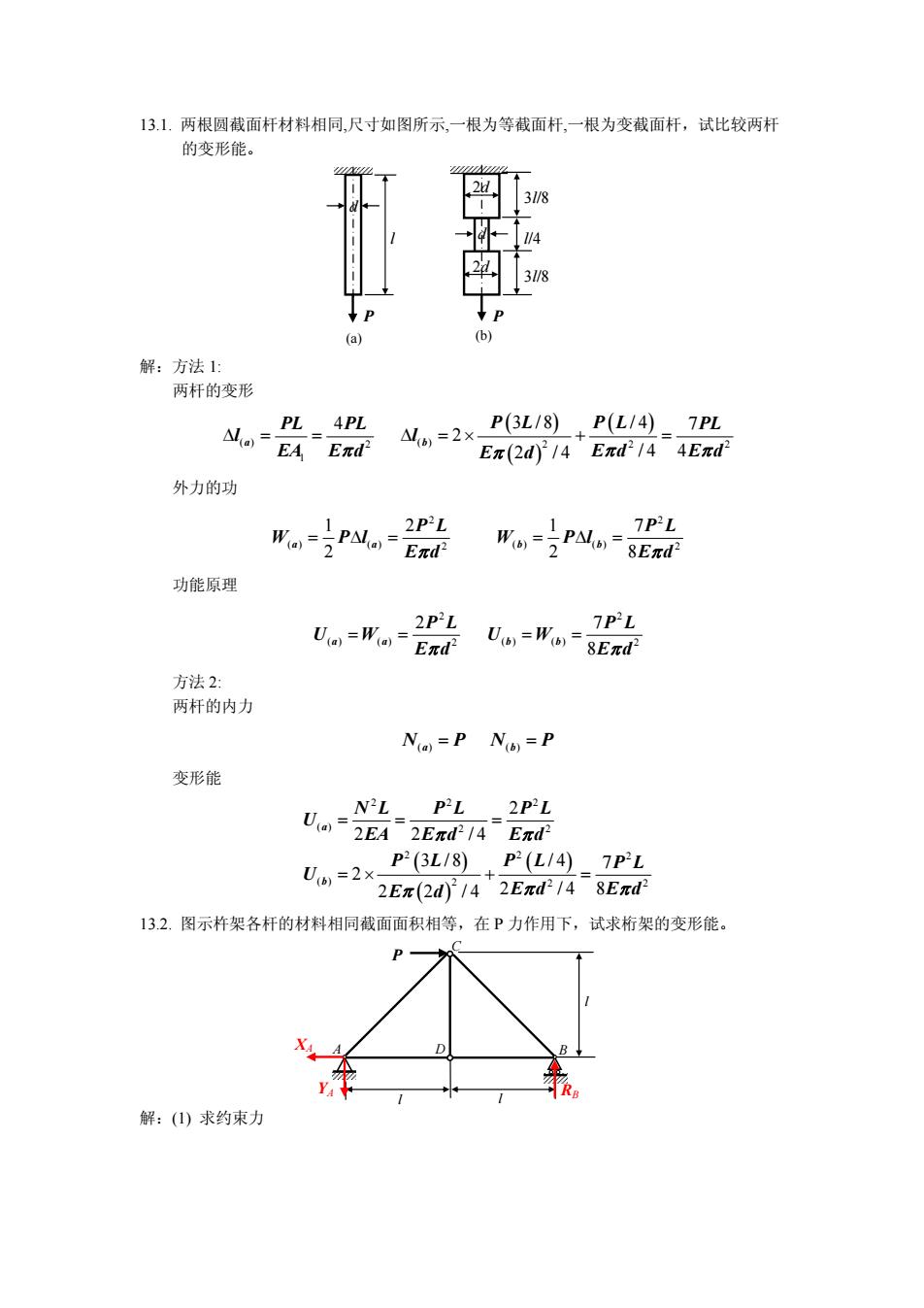
13.1. 两根圆截面杆材料相同,尺寸如图所示,一根为等截面杆,一根为变截面杆,试比较两杆 的变形能。 l 3l/8 d 3l/8 d 2d 2d l/4 P P (a) (b) 解:方法 1: 两杆的变形 ( ) ( ) ( ) ( ) 2 2 ( ) 2 1 4 7 3 /8 /4 2 2 /4 /4 4 a b PL PL P L PL PL l l 2 EA Ed π E d π Ed Ed π π Δ = = Δ =× + = 外力的功 2 2 ( ) ( ) 2 2 ( ) ( ) 12 1 7 2 2 a a b b P L P L W Pl W Pl Eπd E8 πd = Δ= = Δ= 功能原理 2 2 () () 2 2 () () 2 7 8 a a b b P L P L UW UW Eπd Eπd == == 方法 2: 两杆的内力 ( ) ( ) N PN P a b = = 变形能 ( ) ( ) ( ) 22 2 ( ) 2 2 2 2 2 ( ) 2 2 2 2 2 2 /4 3 /8 /4 7 2 2 2 /4 2 /4 8 a b NL PL PL U EA E d E d P L PL P L U E d E d E π π π π πd == = = × + = 13.2. 图示杵架各杆的材料相同截面面积相等,在 P 力作用下,试求桁架的变形能。 RB A D B l l YA XA P C l 解:(1) 求约束力

ZX=0 P-X,=0 X,=PZM^=0 R×21-Pxl=0 Rs=PZY=0 Re-Y=0 Y,=P(2)分析铰BRCNBD +V21Nc=N2R,=NRD=R(3)分析铰DANDNDANNDA=NDe=ND-NDc=0(4)分析铰 CAAV2PNe=Nc =NBc (5)桁架的变形能UZ-ilNlNN)))(((1+)-0.957号=2EAEA2213.3.计算图示各杆的变形能MY21/3(c)解: (b)上海理工大学力学教研室
0 0 0 2 0 2 0 0 2 A A A B B BA A X PX X P P M R l Pl R P Y RY Y = −= = = × − ×= = = −= = ∑ ∑ ∑ (2) 分析铰 B NBC B NBC NBD RB 45o NBD RB 2 2 2 2 BD B BC B P P NR N R == = = (3) 分析铰 D D NDC NDA NDB 0 2 DA DB BD DC P NNN N = == = (4) 分析铰 C NCA P C NCA NCB NCB P 2 2 CA CB BC P NNN === (5) 桁架的变形能 ( ) ( ) 2 22 22 2 2 2 2 1 2 2 1 2 1 2 2 2 2 0.957 2 2 22 2 i i BC BC AC AC BD BD DA DA N l U N l N l N l N l EA EA P P Pl l l P l EA EA = = +++ ⎡ ⎤ ⎛ ⎞ ⎛⎞ ⎛ ⎞ = × × +× × = + = ⎢ ⎥ ⎜ ⎟ ⎜⎟ ⎜ ⎟ ⎝⎠ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ∑ EA 13.3. 计算图示各杆的变形能。 θ ds dθ EI R (c) P B A O A M (b) B EI C l/3 2l/3 解:(b) 上海理工大学 力学教研室 1
方法1:(1)查表得C截面的转角MTe= EN--9E(2)由功能原理M"lU=W=Me =-18EI方法2(1)列出梁的弯矩方程M8LELMI[M(x)=- x,Mx,+MM(x2)=-(2) 求弯曲变形能M’18M1Ml- a+ 2EI162EI162EI18EI(e)(1)列出梁的弯矩方程N(O)M(0)=-PRsino(2) 求弯曲变形能-I s-Irn ro2EI-元P"R8EI13.4.传动轴受力情况如图所示,轴直径为40mm,E=210GPa,G=80GPa。试计算轴的变形能。2上海理工大学力学教研室
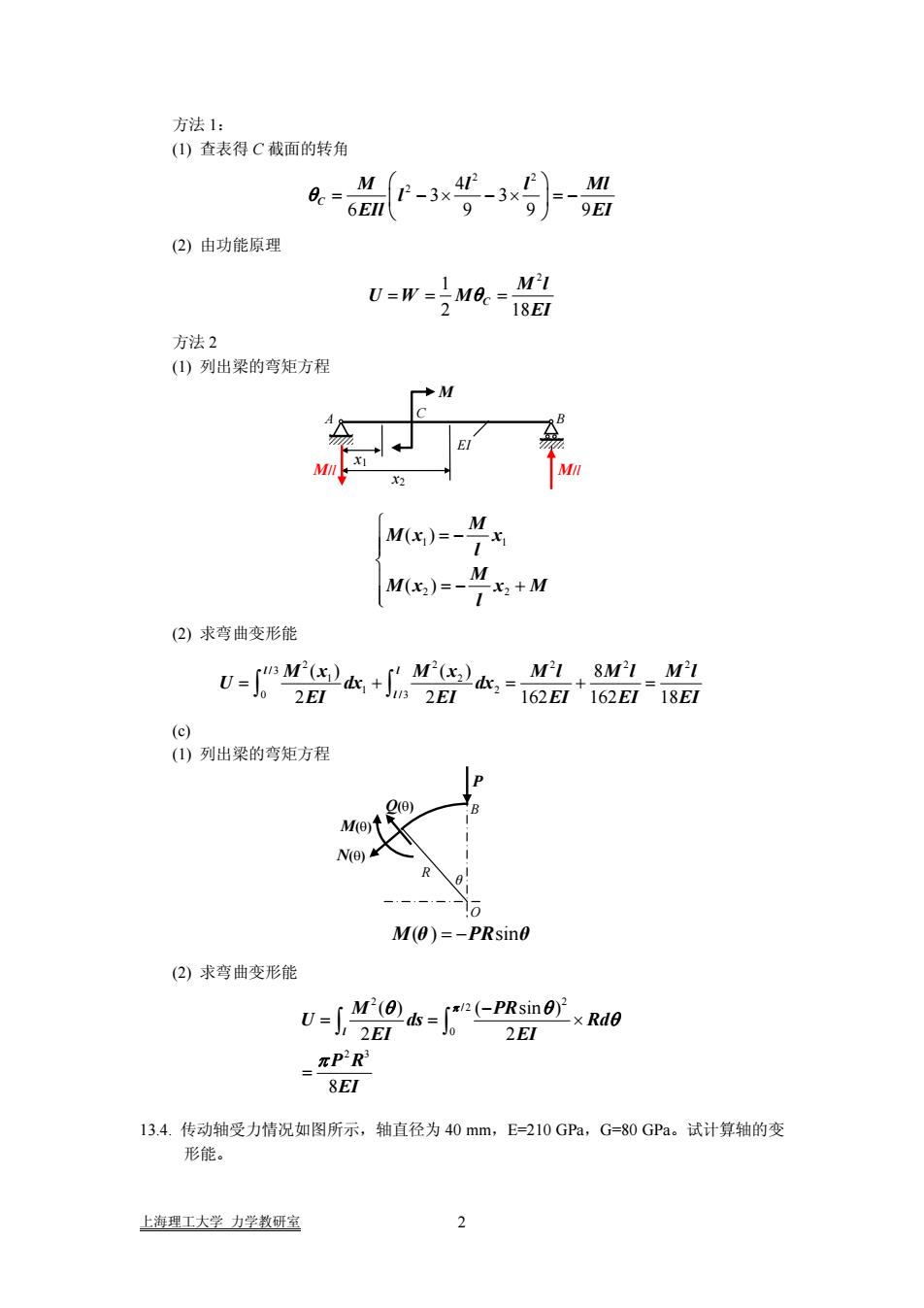
方法 1: (1) 查表得 C 截面的转角 2 2 2 4 3 3 6 99 C M ll l 9 Ml EIl EI θ ⎛ ⎞ = − × − × =− ⎜ ⎟ ⎝ ⎠ (2) 由功能原理 2 1 2 18 C M l UW M EI == = θ 方法 2 (1) 列出梁的弯矩方程 x1 A M B EI C M/l M/l x2 1 1 2 2 ( ) ( ) M Mx x l M Mx x M l ⎧ = − ⎪⎪ ⎨ ⎪ = − + ⎪⎩ (2) 求弯曲变形能 2 22 2 /3 1 2 1 2 0 /3 () () 8 2 2 162 162 18 l l l M x M x Ml Ml Ml U dx dx 2 EI EI EI EI = + =+ ∫ ∫ EI = (c) (1) 列出梁的弯矩方程 M θ )( = −PRsinθ (2) 求弯曲变形能 2 2 / 2 0 2 3 ( ) ( sin ) 2 2 8 l M PR U ds EI EI P R Rd EI θ θ π θ π − == × = ∫ ∫ 13.4. 传动轴受力情况如图所示,轴直径为 40 mm,E=210 GPa,G=80 GPa。试计算轴的变 形能。 θ R P B O Q(θ) M(θ) N(θ) 上海理工大学 力学教研室 2

解:(1)传动轴受力Z.=Z=0.5 kNY, = Yg =0.18 kN(2)弯矩方程和扭矩方程M,(x)=Zgx=500xM,(x)=Y,x=180xT(x)=80(3) 变形能U =2].2J。2GI,2EI(0)+(8))2GIp[500 +180 2)210×10×元×0.04*/643(80) ×0.2+2×80×10×元×0.04*/32=0.0604 J(4)使用功能原理求解本题U=W=↓PS,+PJ+↓ToP3PP1TxTx1/2-T1=1×P,×48E1*2×P×48EI,2a1 e(++ )+,0.4380°×0.41 021010 04 (-0 100)4 0 010 0 -32=0.0604 J13.7.试用互等定理求跨度中点C的挠度,设EI=常量。[P上海理工大学力学教研室
A B 200 C 200 0.08kN.m 0.36kN 1kN 解:(1) 传动轴受力 0.5 0.18 Z Z kN Y Y kN A B = = == A B (2) 弯矩方程和扭矩方程 M x Zx x M x Yx x T x y A zA ( ) = = == = 500 ( ) 180 80 ( ) (3) 变形能 ( ) ( ) ( ) ( ) () () ( ) ( ) 2 2 0.2 0.2 0.2 0 00 2 0.2 0.2 2 2 0 0 3 3 2 2 9 4 2 9 4 500 180 80 2 2 2 22 1 80 0.2 500 180 2 1 0.2 500 180 210 10 0.04 / 64 3 3 80 0.2 2 80 10 0.04 / 32 0.0604 y z P x x U dx dx EI EI GI x dx x dx EI GI J π π =++ × = ++ ⎛ ⎞ = × ⎜ ⎟ × ×× ⎝ ⎠ × + × × ×× = ∫ ∫∫ ∫ ∫ 2 0.2 P dx + × (4) 使用功能原理求解本题 ( ) ( ) 3 3 3 2 2 2 3 2 2 2 9 4 9 4 1 11 2 22 1 1 1/ 2 2 48 2 48 2 96 4 0.4 80 0.4 360 1000 96 210 10 0.04 / 64 4 80 10 0.04 / 32 0.0604 yy zz y z y z y z z yP U W Pf Pf T P l P l Tl l T l P P T PP E P I EI GI EI J φ π π == + + × =× × +× × + × = + + × = + + × × ×× × × ×× = GI 13.7. 试用互等定理求跨度中点 C 的挠度,设 EI=常量。 A B (a) C D a l/2 l/2 P l/2 l/2 P B A C (b) A B YA C 0.36kN 1kN 0.08kN. 0.08kN.m m ZA ZB YB 上海理工大学 力学教研室 3

解:(a)(1)将P力移到C截面处,如下图(2)由位移互等定理PI?Pal?e =81 =8/2 =0g ×a:16E*"16EI方向向上(b) (1)将P力移到C截面处,如下图[P(2)由位移互等定理_P(/2)+[_P(1/2)5PIJe=8 =82= fe+0 ×13EI2EI248EI1方向向下13.8.车床主轴可简化成EI=常量的当量轴,如图所示,试求在载荷P作用下,截面C的挠度和前轴承B处的截面转角。IPYRB解:(1)约束反力Ra=lp Re-2(2) 弯矩方程M(x)=-Px M(x)=-=Px,(3)在C处作用单位集中力 截面C的挠度上海理工大学力学教研室
解:(a) (1) 将 P 力移到 C 截面处,如下图 2 A B C D P 1 (2) 由位移互等定理 2 2 21 12 16 16 C B Pl Pal f aa EI E = = = ×= ×= δδθ I 方向向上 (b) (1) 将 P 力移到 C 截面处,如下图 P B A C 2 1 (2) 由位移互等定理 ( ) ( ) 3 2 3 21 12 /2 /2 5 2 3 2 2 48 C C C l l Pl Pl f f Pl EI EI δδ θ ⎡ ⎤ = = = + × =− + − × =− ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ EI 方向向下 13.8. 车床主轴可简化成 EI=常量的当量轴,如图所示,试求在载荷 P 作用下,截面 C 的挠 度和前轴承 B 处的截面转角。 A B C a P 4a x2 x1 RA RB 解:(1) 约束反力 1 5 4 4 R PR A B = = P (2) 弯矩方程 () ( ) 11 2 1 4 M x Px M x Px = − = − 2 (3) 在 C 处作用单位集中力 11 1 ( ) 2 ( 2 2 ) 1 4 Mx x Mx x = − = − 截面 C 的挠度 A B C 1 x2 x1 1/4 5/4 上海理工大学 力学教研室 4