
3-1.用截面法求图示各杆在截面1-1、2-2、3-3上的扭矩。并于截面上有矢量表示扭矩,指出扭矩的符号。作出各杆扭矩图,(b) 解:(a()用截面法求1-1截面上的扭矩2kN.m JC-2+T, =0Em,=0..T=2kN.m(2)用截面法求2-2截面上的扭矩Tm,=0-2-T,=0:.T, =-2 kN.m(3)画扭矩图2kN.mD(1)用截面法求1-1截面上的扭矩Zm,=0 -T-5+3-2=0.T, = -4 kN.m(2)用截面法求2-2截面上的扭矩T2
3-1. 用截面法求图示各杆在截面 1-1、2-2、3-3 上的扭矩。并于截面上有矢量表示扭矩,指 出扭矩的符号。作出各杆扭矩图。 (b) 5kN.m 3kN.m 2kN.m 1 1 2 2 3 3 2kN.m 1 (a) 4kN.m 2kN.m 1 2 2 解: (a) (1) 用截面法求 1-1 截面上的扭矩 2kN.m 1 1 T1 x 1 1 0 2 0 2 . m T x T kN m = −+ = ∴ = ∑ (2) 用截面法求 2-2 截面上的扭矩 2 2kN.m 2 T2 x 2 2 0 2 0 2 . m T x T kN m = −− = ∴ =− ∑ (3) 画扭矩图 T x 2kN.m 2kN.m (b) (1) 用截面法求 1-1 截面上的扭矩 5kN.m 3kN.m 2kN.m 1 1 T1 x 1 1 0 5 3 2 0 4 . m T x T kN m = − −+−= ∴ =− ∑ (2) 用截面法求 2-2 截面上的扭矩 2 3kN.m 2kN.m 2 T2 x

Zm =0 -T,+3-2=0..T, =1 kNm(3)用截面法求3-3截面上的扭矩Zm,=0-T,-2=0..T, =-2 kN.m(4)画扭矩图KN.2kN.m3.3.直径D=50mm的圆轴受扭矩T=2.15kN.m的作用。试求距轴心10mm处的切应力,并求横截面上的最大切应力。解:(1)圆轴的极惯性矩I-3200%=614×10 m3232点的切应力TP_2.15x10x0.01=35.0MPa6.14×10-71(2)圆轴的抗扭截面系数_614x10=2.456×10~ mW.-DT2~0.052截面上的最大切应力T2.15×103= 87.5 MPaTmaxw,2.456x10-5注:截面上的切应力成线性分布,所以也可以用比例关系求最大切应力。D/2-35.0 005/2=87.5 MPaTmax =t)0.013.4.发电量为1500kW的水轮机主轴如图示。D=550mm,d-300mm,正常转速n=250r/min。材料的许用剪应力[t]=500MPa。试校核水轮机主轴的强度上海理工大学力学教研室
2 2 0 3 2 0 1 . m T x T kN m = − +−= ∴ = ∑ (3) 用截面法求 3-3 截面上的扭矩 3 3 0 2 0 2 . m T x T kN m = − −= ∴ =− ∑ 3 2kN.m 3 T3 x (4) 画扭矩图 T x 1kN.m 2kN.m 4kN.m 3.3. 直径 D=50 mm 的圆轴受扭矩 T=2.15 kN.m 的作用。试求距轴心 10 mm 处的切应力,并 求横截面上的最大切应力。 解: (1) 圆轴的极惯性矩 4 4 32 0.05 7 4 6.14 10 32 32 P D I m π × − = = =× 点的切应力 3 7 2.15 10 0.01 35.0 6.14 10 p T MPa I ρ τ − × × = = = × (2) 圆轴的抗扭截面系数 7 6.14 10 5 3 2.456 10 / 2 0.05/ 2 p t I W m D − × − == =× 截面上的最大切应力 3 max 5 2.15 10 87.5 2.456 10 t T MPa W τ − × == = × 注:截面上的切应力成线性分布,所以也可以用比例关系求最大切应力。 max / 2 0.05/ 2 35.0 87.5 0.01 D τ τ MPa ρ =× = × = 3.4. 发电量为 1500 kW 的水轮机主轴如图示。D=550 mm,d=300 mm,正常转速 n=250 r/min。 材料的许用剪应力[τ]=500 MPa。试校核水轮机主轴的强度。 上海理工大学 力学教研室 1
t轮利解:(1)计算外力偶矩1500 = 57.29 kN.mm=9549_=9549x250(2)计算扭矩T = m= 57.29 kN.m(3)计算抗扭截面系数(Dt- d*)=29.8x10-3 mW =161(4)强度校核T57.29×103=19.2MPa <[α]T=W=29.8x10强度足够。注:强度校核类问题,最后必需给出结论。3-5.图示轴AB的转速i=120T/min,从B轮输入功率P=4.1kW,功率的一半通过锥形齿轮传送给轴C,另一半由水平轴H输出。已知D-60 cm,D=-24cm,dl=10 cm,d=8cm,d=6cm,[tl-20MPa。试对各轴进行强度校核。akI解:(1)计算外力偶矩x44.1 =3509 N.mP=9549m= 9549.120Im=1755 N.mmu=44.1R=9549-= 701.9 N.mmc= 9549D8 120DixnD上海理工大学力学教研室
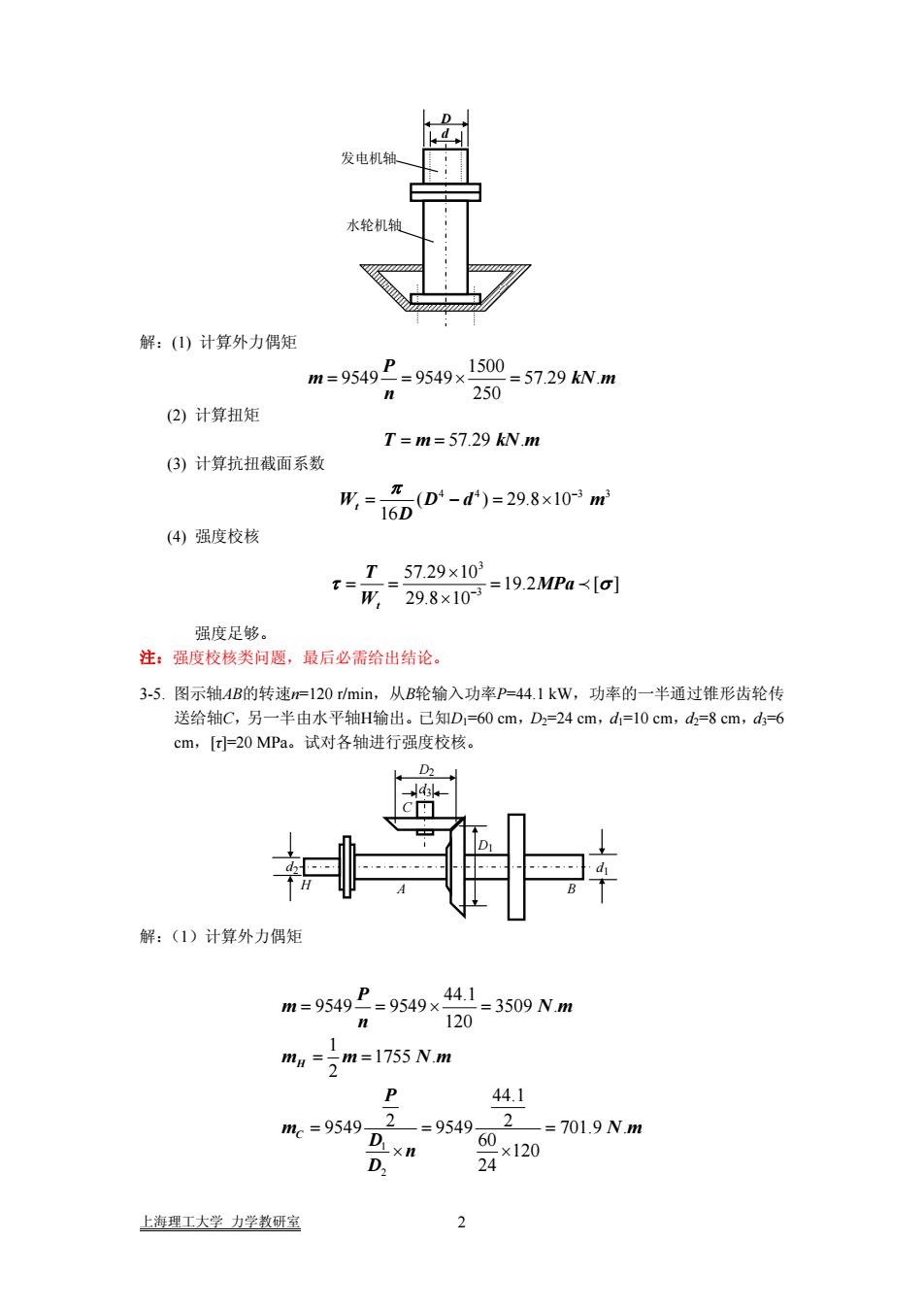
d D 发电机轴 水轮机轴 解:(1) 计算外力偶矩 1500 9549 9549 57.29 . 250 P m k n = =×= N m (2) 计算扭矩 T m kN m = = 57.29 . (3) 计算抗扭截面系数 4 4 3 ( ) 29.8 10 16 W Dd t D 3 m π − = −= × (4) 强度校核 3 3 57.29 10 19.2 [ ] 29.8 10 t T MPa W τ σ − × == = × ≺ 强度足够。 注:强度校核类问题,最后必需给出结论。 3-5. 图示轴AB的转速n=120 r/min,从B轮输入功率P=44.1 kW,功率的一半通过锥形齿轮传 送给轴C,另一半由水平轴H输出。已知D1=60 cm,D2=24 cm,d1=10 cm,d2=8 cm,d3=6 cm,[τ]=20 MPa。试对各轴进行强度校核。 d2 d1 d3 D1 D2 H A B C 解:(1)计算外力偶矩 1 2 44.1 9549 9549 3509 . 120 1 1755 . 2 44.1 2 2 9549 9549 701.9 . 60 120 24 H C P m N n m m Nm P m N D n D = =×= = = == = × × m m 上海理工大学 力学教研室 2

(2)计算内力扭矩Tas=m=3509N.mTh=mz=1755NmT = mc = 701.9N.m(3)计算抗扭截面系数Wun==×0. P=196×10~ mWa=4×0.08=10010~mWc--×0.06=42.4x10-m(4)强度校核3509T=17.9MPa<[t]TABmWuB"196x10-1755IL=17.55MPa[]HmayW.100×10-6A701.9= 16.55 MPa [1]tcmaxWic42.4×10%c强度足够。3-6.图示阶梯形圆轴直径分别为d=40mm,d=70mm,轴上装有三个带轮。已知由轮3输入的功率为P;=30kW,轮1输出的功率为P,=13kW,轴作匀速转动,转速n=200r/min材料的许用剪应力[t}-60 MPa,G=80 GPa,许用扭转角[9]-2%m。试校核轴的强度和冈度。C.dco0.5m 10.3ml解:(1)计算外力偶矩m =9549号-9549×20013=620.7Nmm =9549 =9549× 30=1432.4Nm200(2)计算扭矩T, =-m =-620.7 N.m=-m=-1432.4N.mTIkN.n620.7N.m432.47上海理工大学力学教研室
(2)计算内力扭矩 3509 . 1755 701.9 . AB H H C C T m Nm T m N T m Nm = = = = = = m (3)计算抗扭截面系数 33 6 1 3 36 2 3 3 3 0.1 196 10 16 16 0.08 100 10 16 16 0.06 42.4 10 16 16 tAB tH tC W d m W d W d 3 3 6 3 m m π π π π π π − − − = =× = × = =× = × = =× = × (4)强度校核 max 6 max 6 max 6 3509 17.9 [ ] 196 10 1755 17.55 [ ] 100 10 701.9 16.55 [ ] 42.4 10 AB AB tAB H H tH C C tC tC T MPa W T MPa W T MPa W τ τ τ τ τ τ − − − == = × == = × == = × ≺ ≺ ≺ 强度足够。 3-6. 图示阶梯形圆轴直径分别为d1=40 mm,d2=70 mm,轴上装有三个带轮。已知由轮 3 输 入的功率为P3=30 kW,轮 1 输出的功率为P1=13 kW,轴作匀速转动,转速n=200 r/min, 材料的许用剪应力[τ]=60 MPa,G=80 GPa,许用扭转角[θ]=2 o /m。试校核轴的强度和刚 度。 m2 m3 解:(1) 计算外力偶矩 1 1 3 3 13 9549 9549 620.7 200 30 9549 9549 1432.4 200 P m N n P m N n = = ×= = = ×= m m (2) 计算扭矩 12 1 23 3 T m Nm T m Nm =− =−620.7 . =− =−1432.4 . m1 A 1 C B 2 3 0.5m 1m D d2 d1 0.3m T x 1kN.m 1432.4N.m 620.7N.m 上海理工大学 力学教研室 3

(3)计算抗扭截面系数元×0.043=12.56×10-mWa=d=Wa-"d,--元×0.073=67.31×10~m(4)强度校核620.7112 1. 5010-4.42MPa[] Tmax1 =1432.4T23 =21.28MPa≤[] Tmax2 =w,z67.31x10-6强度足够。5)计算截面极惯性矩 =12.56×10~×0.04Ipr=W,x4= 25.12×10-8 m=67.31×1023.56×107mIn=W,x2(6)刚度校核T2180°620.7180° =1.77° / m [0]Omaxl= Gl,80×10°×25.12×10-8元元1432.4T2s180°x180° =0.435 m [0]0max2=元80×10°×23.56×10-7×GIp2刚度足够。注:本题中扭矩的符号为负,而在强度和刚度计算中,扭矩用其数值代入。3.9,实心轴和空心轴由牙嵌式离合器连接在一起,如图所示。已知轴的转速为n=100r/min传递的功率P=7.5kW,材料的许用剪应力[t]=40MPa。试选择实心轴直径d;和内外径比值为1/2的空心轴外径D2。--解:(1)计算外力偶矩x75=716.2N.mm=9549=9549x100(2)计算内力-扭矩T = m= 716.2N.m(3)计算抗扭截面系数上海理工大学力学教研室
(3) 计算抗扭截面系数 3 3 1 1 3 3 2 2 0.04 12.56 10 16 16 0.07 67.31 10 16 16 t t W d W d 6 3 6 3 m m π π π π − − = =× = × = =× = × (4) 强度校核 [ ] [ ] 12 max1 6 1 23 max 2 6 2 620.7 49.42 12.56 10 1432.4 21.28 67.31 10 t t T MPa W T MPa W τ τ τ τ − − == = ≤ × == = ≤ × 强度足够。 (5) 计算截面极惯性矩 1 6 8 1 1 2 6 7 2 2 0.04 12.56 10 25.12 10 2 2 0.07 67.31 10 23.56 10 2 2 p t p t d 4 3 I W m d I W m − − − − = ×= × × = × = ×= × × = × (6) 刚度校核 12 max1 9 8 1 23 max 2 9 7 2 180 620.7 180 1.77 / [ ] 80 10 25.12 10 180 1432.4 180 0.435 / [ ] 80 10 23.56 10 o o o p o o o p T m GI T m GI θ θ π π θ θ π π − − =×= × = ×× × =×= × = ×× × ≺ ≺ 刚度足够。 注:本题中扭矩的符号为负,而在强度和刚度计算中,扭矩用其数值代入。 3.9. 实心轴和空心轴由牙嵌式离合器连接在一起,如图所示。已知轴的转速为n=100 r/min, 传递的功率P=7.5 kW,材料的许用剪应力[τ]=40 MPa。试选择实心轴直径d1和内外径 比值为 1/2 的空心轴外径D2。 D2 d2 d1 解:(1) 计算外力偶矩 7.5 9549 9549 716.2 . 100 P m N n = = ×= m (2) 计算内力-扭矩 T m Nm = = 716.2 . (3) 计算抗扭截面系数 上海理工大学 力学教研室 4