
6.1.矩形截面悬臂梁如图所示,已知F=4m,b/h=2/3,9-10kN/m,[]=10MPa,试确定此梁横截面的尺寸。口解:(1)画梁的弯矩图MTt'12由弯矩图知:qMmar(2)计算抗弯截面系数br号nW-69(3)强度计算ql9gt,M2[]h:h29g19×10×10×42=416mm2[02×10x10%b≥277mm6.2.20a工字钢梁的支承和受力情况如图所示,若[o]=160MPa,试求许可载荷IP-I:aNo20aP解:(1)画梁的弯矩图由弯矩图知:
6.1. 矩形截面悬臂梁如图所示,已知 l=4 m, b / h =2/3,q=10 kN/m,[σ]=10 MPa,试确 定此梁横截面的尺寸。 q l b h 解:(1) 画梁的弯矩图 M ql2 /2 (-) x 由弯矩图知: 2 max 2 ql M = (2) 计算抗弯截面系数 3 2 3 2 3 6 6 h bh h W == = 9 (3) 强度计算 2 2 max max 3 3 2 3 2 3 3 6 9 1 2 [ ] 2 9 9 9 10 10 4 416 2[ ] 2 10 10 277 ql M ql W h h ql h m b mm σ σ σ = = = ⋅≤ ×× × ∴≥ = = × × ≥ m 6.2. 20a 工字钢梁的支承和受力情况如图所示,若[σ]=160 MPa,试求许可载荷。 A P P C D B 2m 2m 2m No20a 解:(1) 画梁的弯矩图 M 2P/3 2P/3 x (+) (-) 由弯矩图知:

2PMma(2)查表得抗弯截面系数W=237x10-°m(3)强度计算2PMmax-2-P≤[0]-3Omax3W p /al_ 23x10 1010 - 68取许可载荷[P]=57kN6.3.图示圆轴的外伸部分系空心轴。试作轴弯矩图,并求轴内最大正应力。解:(1)画梁的弯矩图由弯矩图知:可能危险截面是C和B截面(2)计算危险截面上的最大正应力值C截面:32x1.34x10mMcM.=63.2MPaOcmax元×0.063Wcnd32B截面0.9×103M.1x006α 045=62.1MPaOBmWB320.064Dt(3)轴内的最大正应力值0 mx =0 cmx =63.2MPa上海理工大学力学教研室
max 2 3 P M = (2) 查表得抗弯截面系数 6 3 W m 237 10− = × (3) 强度计算 max max 6 6 2 3 2 [ ] 3 3 [ ] 3 237 10 160 10 56.88 2 2 P M P W WW W P k σ σ σ − = = = ⋅≤ × × ×× ∴≤ = = N N 取许可载荷 [ ] 57 P k = 6.3. 图示圆轴的外伸部分系空心轴。试作轴弯矩图,并求轴内最大正应力。 400 800 200 300 5kN 3kN 3kN φ60 φ45 A C D B E 解:(1) 画梁的弯矩图 M 1.34kNm x (+) (-) 0.9kNm 由弯矩图知:可能危险截面是 C 和 B 截面 (2) 计算危险截面上的最大正应力值 C 截面: 3 max 3 3 32 1.34 10 63.2 0.06 32 C C C C C M M MPa W d σ π π × × == = = × B 截面: 3 max 34 3 4 4 4 0.9 10 62.1 0.06 0.045 (1 ) (1 ) 32 32 0.06 B B B B B B B M M MPa W D d D σ π π × == = = × − − (3) 轴内的最大正应力值 MPa C 2.63 max =σσ max = 上海理工大学 力学教研室 1

6.5.把直径d-1m的钢丝绕在直径为2m的卷筒上,设E=200GPa,试计算钢丝中产生的最大正应力解:(1)由钢丝的曲率半径知1_M.E-MP"EL0(2)钢丝中产生的最大正应力_ MR_ ER_ 200×10×0.5×10-=100 MPagmax1p6.8.压板的尺寸和载荷如图所示。材料为45钢,o=380MPa,取安全系数n=1.5。试校核压板的强度。解:(1)画梁的弯矩图由弯矩图知:危险截面是A截面,截面弯矩是M,=308Nm(2)计算抗弯截面系数_bH"(--h)0.03×0.022(12)=1.568×10-mW:H620(3)强度计算许用应力[01-0- 0- 23MPa1.5强度校核M308=196MPa ^[α]gmax1.568×10W压板强度足够。上海理工大学力学教研室
6.5. 把直径 d=1 m 的钢丝绕在直径为 2 m 的卷筒上,设 E=200 GPa,试计算钢丝中产生的 最大正应力。 解:(1) 由钢丝的曲率半径知 1 M E M ρ ρ EI I = ∴= (2) 钢丝中产生的最大正应力 9 3 max 200 10 0.5 10 100 1 MR ER MPa I σ ρ − ××× = == = 6.8. 压板的尺寸和载荷如图所示。材料为 45 钢,σs=380 MPa,取安全系数n=1.5。试校核压 板的强度。 20 38 A A φ12 20 30 P1=15.4kN A-A 解:(1) 画梁的弯矩图 M 308Nm x (+) 由弯矩图知:危险截面是 A 截面,截面弯矩是 308 M N A = m (2) 计算抗弯截面系数 2 3 2 3 6 3 3 3 0.03 0.02 12 (1 ) (1 ) 1.568 10 6 620 bH h W m H × − = −= −= × (3) 强度计算 许用应力 380 [ ] 253 1.5 S MPa n σ σ == = 强度校核 max 6 308 196 [ ] 1.568 10 MA MPa W σ σ − == = × ≺ 压板强度足够。 上海理工大学 力学教研室 2
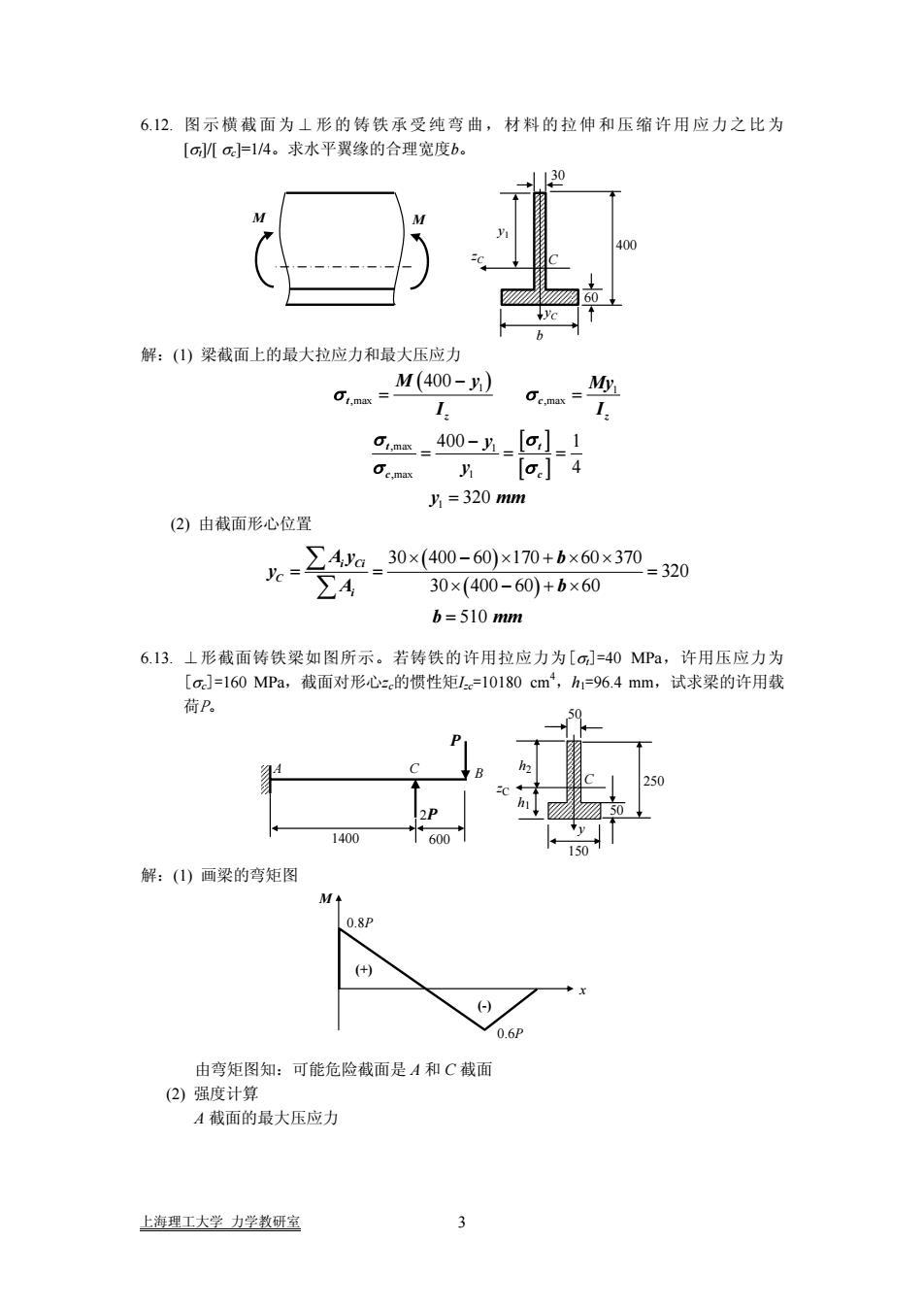
6.12.图示横截面为工形的铸铁承受纯弯曲,材料的拉伸和压缩许用应力之比为[o][o.]-1/4。求水平翼缘的合理宽度b。解:(1)梁截面上的最大拉应力和最大压应力M(400 -)Jt.momI.mm_ 400-y_[o,]_ ][.] 4Oc.maxJf=320 mm(2)由截面形心位置ZAya_ 30×(40060)×170+b×60×370 = 320c30×(400-60)+b×60Z4b=510mm6.13.形截面铸铁梁如图所示。若铸铁的许用拉应力为[o]=40MPa,许用压应力为[]=160MPa,截面对形心=。的惯性矩Ic=10180cm,hi=96.4mm,试求梁的许用载荷P。T42P600解:(1)画梁的弯矩图06由弯矩图知:可能危险截面是A和C截面(2)强度计算A截面的最大压应力上海理工大学力学教研室3
6.12. 图示横截面为⊥形的铸铁承受纯弯曲,材料的拉伸和压缩许用应力之比为 [σt]/[ σc]=1/4。求水平翼缘的合理宽度b。 400 30 60 zC yC b C M M y1 解:(1) 梁截面上的最大拉应力和最大压应力 ( ) [ ] [ ] 1 1 ,max ,max ,max 1 ,max 1 1 400 400 1 4 320 t c z z t t c c M y My I I y y y mm σ σ σ σ σ σ − = = − = == = (2) 由截面形心位置 ( ) ( ) 30 400 60 170 60 370 320 30 400 60 60 510 i Ci C i A y b y A b b mm × − × +× × = = = × − +× = ∑ ∑ 6.13. ⊥形截面铸铁梁如图所示。若铸铁的许用拉应力为[σt]=40 MPa,许用压应力为 [σc]=160 MPa,截面对形心zc的惯性矩Izc=10180 cm 4 ,h1=96.4 mm,试求梁的许用载 荷P。 P 50 1400 600 2P A C B 250 150 50 h1 h2 zC y C 解:(1) 画梁的弯矩图 M 0.8P x (+) (-) 0.6P 由弯矩图知:可能危险截面是 A 和 C 截面 (2) 强度计算 A 截面的最大压应力 上海理工大学 力学教研室 3

Mh _08Ph ≤[0]acmaIicI.c. sglal-1018010*x10x10-1326kN0.8(250-96.4)×100.8hA截面的最大拉应力_0.8Ph ≤[0,]M.hfmaxI.I.c0.8h0.8×96.4×10-3C截面的最大拉应力_0.6Ph ≤[0,]M.h,T1.clo]_10180×10×40×10%06(250-964)-442NP0.6h取许用载荷值[P]= 44.2kN6.14.铸铁梁的载荷及截面尺寸如图所示。许用拉应力[o]=40MPa,许用压应力[a]=160MPa。试按正应力强度条件校核梁的强度。若载荷不变,但将T形截面倒置成为工形,是否合理?何故?200P=20kN解:(1)画梁的弯矩图由弯矩图知:可能危险截面是B和C截面(2)计算截面几何性质形心位置和形心惯性矩4m_30×20×21±20030×100=1575 mc30×200+200×30Z4I c=J,jdA= [17s ×30×dy+J,y×200×dy=60.125x10~m上海理工大学力学教研室4
( ) 2 2 max 8 6 3 2 0.8 [ ] [ ] 10180 10 160 10 132.6 0.8 0.8 250 96.4 10 A C C zC zC zC C M h Ph I I I P kN h σ σ σ − − == ≤ × ×× ∴≤ = = − × A 截面的最大拉应力 1 1 max 8 6 3 1 0.8 [ ] [ ] 10180 10 40 10 52.8 0.8 0.8 96.4 10 A t t zC zC zC t M h Ph I I I P kN h σ σ σ − − == ≤ × ×× ∴≤ = = × × C 截面的最大拉应力 ( ) 2 2 max 8 6 3 2 0.6 [ ] [ ] 10180 10 40 10 44.2 0.6 0.6 250 96.4 10 C t t zC zC zC t M h Ph I I I P k h σ σ σ − − == ≤ × ×× ∴≤ = = − × N N 取许用载荷值 [ ] 44.2 P k = 6.14. 铸铁梁的载荷及截面尺寸如图所示。许用拉应力[σl]=40 MPa,许用压应力[σc]=160 MPa。试按正应力强度条件校核梁的强度。若载荷不变,但将T形截面倒置成为⊥形, 是否合理?何故? 解:(1) 画梁的弯矩图 A P=20kN B C D 2m 3m 1m q=10kN/m 200 200 30 30 zC y yC C M 20kNm x (+) (-) 10kNm 由弯矩图知:可能危险截面是 B 和 C 截面 (2) 计算截面几何性质 形心位置和形心惯性矩 42.5 72.5 22 2 157.5 42.5 30 200 215 200 30 100 157.5 30 200 200 30 30 200 60.125 10 i Ci C i zC A A y y m A 6 4 m I y dA y dy y dy m− − × × + ×× = = = ×+× = = ××+ × ×= × ∑ ∑ ∫∫ ∫ 上海理工大学 力学教研室 4