
7.2.用积分法求图示各梁的挠曲线方程、自由端的截面转角,跨度中点的挠度和最大挠度。设EI=常量解: (b)(1)列弯矩方程[M(x)=-PxX, E[0,a][M(s)=-Px, -P(x, -a) x E[a,2a)(2)曲线近似微分方程[EIv} = M,(x) = -Px,[EIv, = M,(x2) =-Px, - P(x -0)(3)直接积分两次Elv =+C(x -a)° +C,Elv,EIy:-x +Cx, + D,(x, -a) +C,x, +D,Elv,(4)确定积分常数边界条件:x=2a: V=0, =0光滑连续条件:X=x,=a? =v2, =v求解得积分常数a" D,=D,=-PaC,=C,=号Pa梁的挑曲线方程和转角方程是
7.2. 用积分法求图示各梁的挠曲线方程、自由端的截面转角,跨度中点的挠度和最大挠度。 设 EI=常量。 P a a P A B C (b) q l/2 l/2 A B C (c) 解:(b) (1) 列弯矩方程 P P A B x1 C x2 11 1 1 22 2 2 2 ( ) [0, ] ( ) ( ) [ ,2 ) M x Px x a M x Px P x a x a a ⎧ =− ∈ ⎨ ⎩ =− − − ∈ (2) 挠曲线近似微分方程 " 1 11 1 " 2 22 2 2 ( ) () ( ) EIv M x Px EIv M x Px P x a ⎧⎪ = =− ⎨ ⎪⎩ = =− − − (3) 直接积分两次 ' 2 1 11 '2 2 2 22 2 ( ) 2 2 P EIv x C P P E 2 Iv x x a C ⎧ =− + ⎪⎪ ⎨ ⎪ =− − − + ⎪⎩ 3 1 1 11 1 3 3 2 2 2 22 6 ( ) 6 6 P EIv x C x D P P E 2 Iv x x a C x D ⎧ =− + + ⎪⎪ ⎨ ⎪ =− − − + + ⎪⎩ (4) 确定积分常数 边界条件: ' 2 22 x av v = 2 : 0, 0 = = 光滑连续条件: ' ' 1 2 12 12 xxa vv vv = = == : , 求解得积分常数 3 21 2 21 2 7 2 5 == −== PaDDPaCC 梁的挠曲线方程和转角方程是

[Ei=-x+pa?Ev,--x-(,-a)+Pa[Ey =-x+Pax--Pa[En---a-) pix-p(5)自由端的转角、跨度中点的揽度和最大挠度x=0:Jns=) =-7Pd,0,=m=SPa2EI2EI令x=a:-注:挠度方向向下,转角为逆时针转向。c)(1)求约束反力并列出弯矩方程“AR-- M-M(x)=-3+号xe(0)[M(a)-- eg,(2)挠曲线近似微分方程[E = M(a)--3++x[Eng =M(s)=-(--)(3)直接积分两次上海理工大学力学教研室
' 22 1 1 '2 2 2 22 5 2 2 5 ( ) 22 2 P EIv x Pa P P 2 EIv x x a Pa ⎧ =− + ⎪⎪ ⎨ ⎪ =− − − + ⎪⎩ 32 3 11 1 3 32 2 22 2 5 7 62 2 5 7 ( ) 66 2 2 P EIv x Pa x Pa P P 3 EIv x x a Pa x Pa ⎧ =− + − ⎪⎪ ⎨ ⎪ =− − − + − ⎪⎩ (5) 自由端的转角、跨度中点的挠度和最大挠度 令x1=0: 3 2 ' max 1 1 7 5 , 2 2 A Pa P f v v a EI E = =− = = θ I 令x1=a: 3 1 7 6 C Pa f v EI = =− 注:挠度方向向下,转角为逆时针转向。 (c) (1) 求约束反力并列出弯矩方程 x1 x2 q A B C RA MA 2 3 2 8 A A ql ql R M = = ( ) 2 1 1 1 1 2 2 2 2 2 3 ( ) (0, ] 82 2 ( ) [ , ] 2 2 ql ql l M x x x ql x l M x x l ⎧ ⎪ =− + ∈ ⎪ ⎨ ⎪ − = − ∈ ⎪⎩ (2) 挠曲线近似微分方程 ( ) 2 " 1 11 2 " 2 2 22 3 ( ) 8 2 ( ) 2 ql ql E 1 Iv M x x ql x EIv M x ⎧ = =− + ⎪ ⎪ ⎨ ⎪ − = =− ⎪⎩ (3) 直接积分两次 上海理工大学 力学教研室 1

[EW=-x+x+,[Eng = (l-x)+C[EW=--x++Cx+D[Em-+ + 24(4)确定积分常数边界条件:x=0: =0, =0光滑连续条件:X=x, =1=v2, =y求解得积分常数D, = 15glG=D,=0 C,=-7q38448梁的挠曲线方程和转角方程是[Em =--3 x+x[Em - (-- 7[Em--x+2448(5)自由端的转角、跨度中点的挠度和最大挠度令x;=l:41q0,=y;=- 7glJmax = V, =-384EI48EI令x=1/2:7ql4fc=y :192EI7.4.求图示等截面悬臂梁的挠曲线方程,自由端的挠度和转角。求解时应注意到梁在CB段内无载荷,故CB仍为直线。上海理工大学力学教研室
( ) 2 ' 2 1 11 3 ' 2 2 2 3 8 4 6 ql ql E 1 Iv x x C ql x EIv C ⎧ = − ++ ⎪ ⎪ ⎨ ⎪ − = + ⎪⎩ ( ) 2 2 3 1 1 11 1 4 2 2 2 2 3 16 12 24 ql ql 1 2 EIv x x C x D ql x EIv C x D ⎧ = − + ++ ⎪ ⎪ ⎨ ⎪ − =− + + ⎪⎩ (4) 确定积分常数 边界条件: ' 1 11 x vv = 0: 0, 0 = = 光滑连续条件: ' ' 1 2 12 1 : , 2 l xx vv vv = = = = 2 求解得积分常数 3 4 11 2 2 7 1 0 48 384 ql ql CD C D = = =− = 5 梁的挠曲线方程和转角方程是 ( ) 2 ' 2 1 1 3 3 ' 2 2 3 8 4 7 6 4 ql ql 1 8 EIv x x ql x ql EIv ⎧ =− + ⎪ ⎪ ⎨ ⎪ − = − ⎪⎩ ( ) 2 2 3 1 11 4 3 4 2 2 2 3 16 12 7 15 24 48 384 ql ql EIv x x ql x ql ql EIv x ⎧ =− + ⎪ ⎪ ⎨ ⎪ − =− − + ⎪⎩ (5) 自由端的转角、跨度中点的挠度和最大挠度 令x1=l: 4 3 ' max 2 2 41 7 , 384 48 B ql ql f v v EI E = =− = =− θ I 令x1=l/2: 4 1 7 192 C ql f v EI = =− 7.4. 求图示等截面悬臂梁的挠曲线方程,自由端的挠度和转角。求解时应注意到梁在 CB 段 内无载荷,故 CB 仍为直线。 上海理工大学 力学教研室 2

P解:(1)求约束反力R,=PMA= Pa(2)列AC段的弯矩方程M(x)=Px- Paxe(0,a)(3)曲线近似微分方程EIv"= M(x)= Px - Pa(4)直接积分两次EIv- Pax +CEly*?+Cx+D(5)确定积分常数边界条件:x=0: v=v=0得积分常数:C=D=0(6)AC段的挠曲线方程和转角方程Elv'-PaxEIV()C截面的挠度和转角令x-a:Pa?Pa30.fc=-2EI3EI(8)自由端的挠度和转角梁的变形:上海理工大学力学教研室n
a l P (a) 解:(1) 求约束反力 A B C P MA RPMP A A = = a (2) 列 AC 段的弯矩方程 M x Px Pa x a ( ) (0, ] = − ∈ (3) 挠曲线近似微分方程 EIv M x Px Pa '' ( ) = = − (4) 直接积分两次 2 3 2 ' 2 6 2 P EIv x Pax C P Pa EIv x x Cx D = −+ = − ++ (5) 确定积分常数 边界条件: x vv = 0: ' 0 = = 得积分常数: C D= = 0 (6) AC 段的挠曲线方程和转角方程 2 3 2 ' 2 6 2 P EIv x Pax P Pa EIv x x = − = − (7) C 截面的挠度和转角 令 x=a: 2 3 2 3 C C Pa P f a EI E θ =− =− I (8) 自由端的挠度和转角 梁的变形: RA x 上海理工大学 力学教研室 3
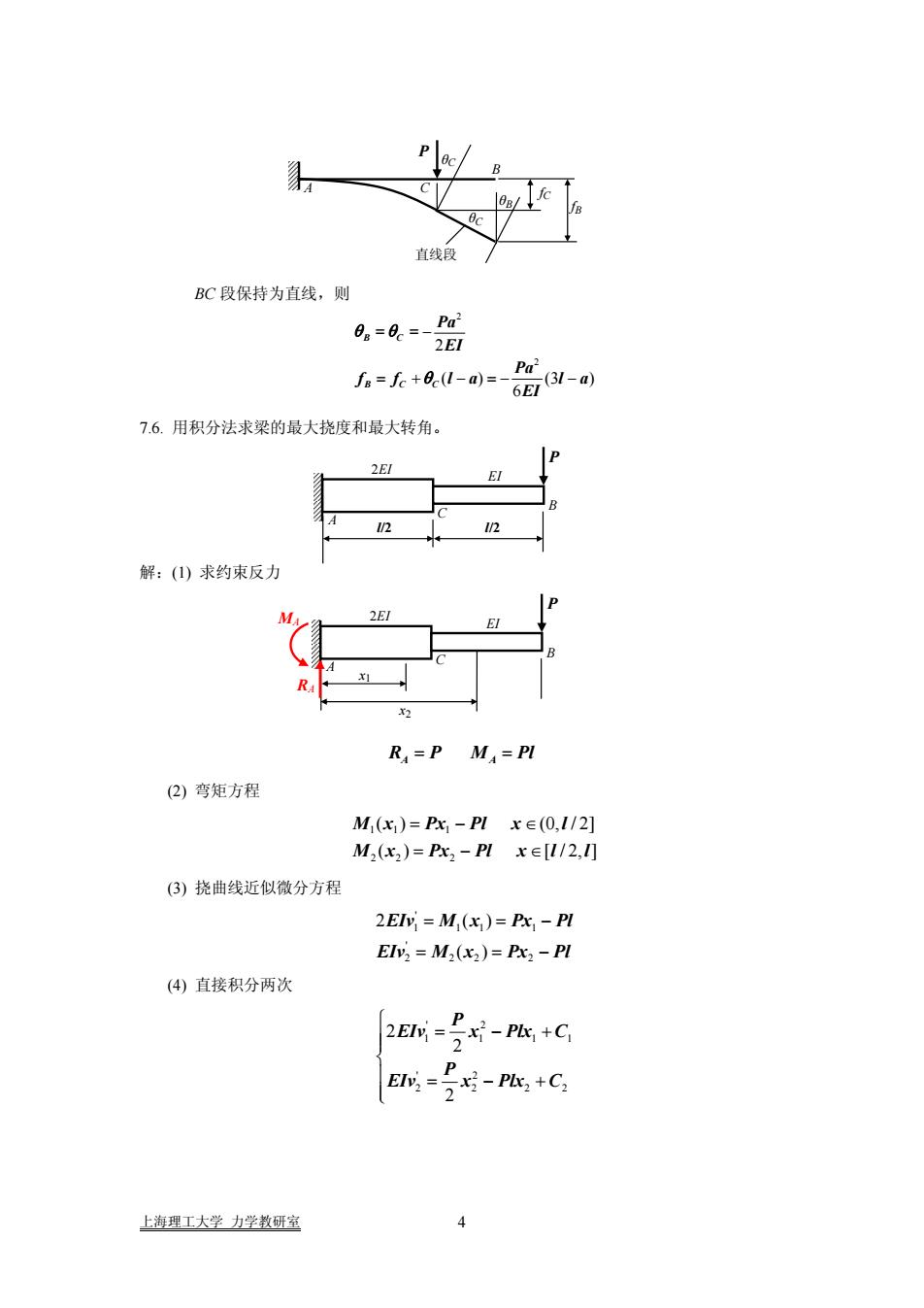
目线用BC段保持为直线,则0. - -_Pa(31 -a)Je= fe +0c(I-a)=-7.6.用积分法求梁的最大挠度和最大转角。解:(1)求约束反力R,=P M=Pl(2)弯矩方程M(x)= Px, - PIxe (0,1/2)M,(x,)=Px, -Pl xE[1/2,1](3)挠曲线近似微分方程2EIv = M,(x)= Px - PIElvz = M2(x2)= Px2 - PI(4)直接积分两次x - Plx; +C,EIv, =-Plx,+Cy上海理工大学力学教研室
BC 段保持为直线,则 2 2 2 ( ) (3 6 B C B CC Pa EI Pa f f la la EI θ θ θ = = − = + − =− − ) l 7.6. 用积分法求梁的最大挠度和最大转角。 l/2 P A B C l/2 EI 2EI P A B C fC θC θC θB fB 直线段 解:(1) 求约束反力 x2 RPMP A A = = (2) 弯矩方程 11 1 22 2 ( ) (0, / 2] ( ) [ / 2, ] M x Px Pl x l M x Px Pl x l l = − ∈ =− ∈ (3) 挠曲线近似微分方程 ' 1 11 1 ' 2 22 2 2 () ( ) EIv M x Px Pl EIv M x Px Pl = = − = =− (4) 直接积分两次 ' 2 111 ' 2 2 22 2 2 2 P 1 2 EIv x Plx C P EIv x Plx C ⎧ = − + ⎪⎪ ⎨ ⎪ = −+ ⎪⎩ RA MA x1 P A B C EI 2EI 上海理工大学 力学教研室 4