
第二章 拉伸、压缩与剪切第二章拉伸、压缩与剪切2.1求图示各杆指定截面的轴力,并作轴力图。(a)解:4 40kN 3 50kN 225kN 1_20kNHFOTFr=5kNF4. FN.F40kN 3FRENFN=Fr=5 kNFN,=FR+40=45 kN225kN20kNF20kMFNFN=-25+20-5 kNFN,=20kN45kN20kN5kN田田SLN
第二章 拉伸、压缩与剪切 3 第二章 拉伸、压缩与剪切 2.1 求图示各杆指定截面的轴力,并作轴力图。 FR 40kN 50kN 25kN 1 20kN 2 1 2 3 3 4 4 (a) 4 4 FR FN4 40kN 3 FR FN3 25kN 20kN 2 2 FN2 1 20kN 1 FN1 解: FR=5kN FN4=FR=5 kN FN3=FR+40=45 kN FN2=-25+20=-5 kN FN1=20kN 45kN 5kN 20kN 5kN
第二章 拉伸、压缩与剪切10kN26kN10kN6kN1-1截面;(b)FN,=10 kN10kN2—2截面;FN=10-10=010kN10kN3—3截面:Fn=6 kNFN6kN10kN6kN田田2.2图示一面积为100mm×200mm的矩形截面杆,受拉力F=20kN的作用,试求:(1)
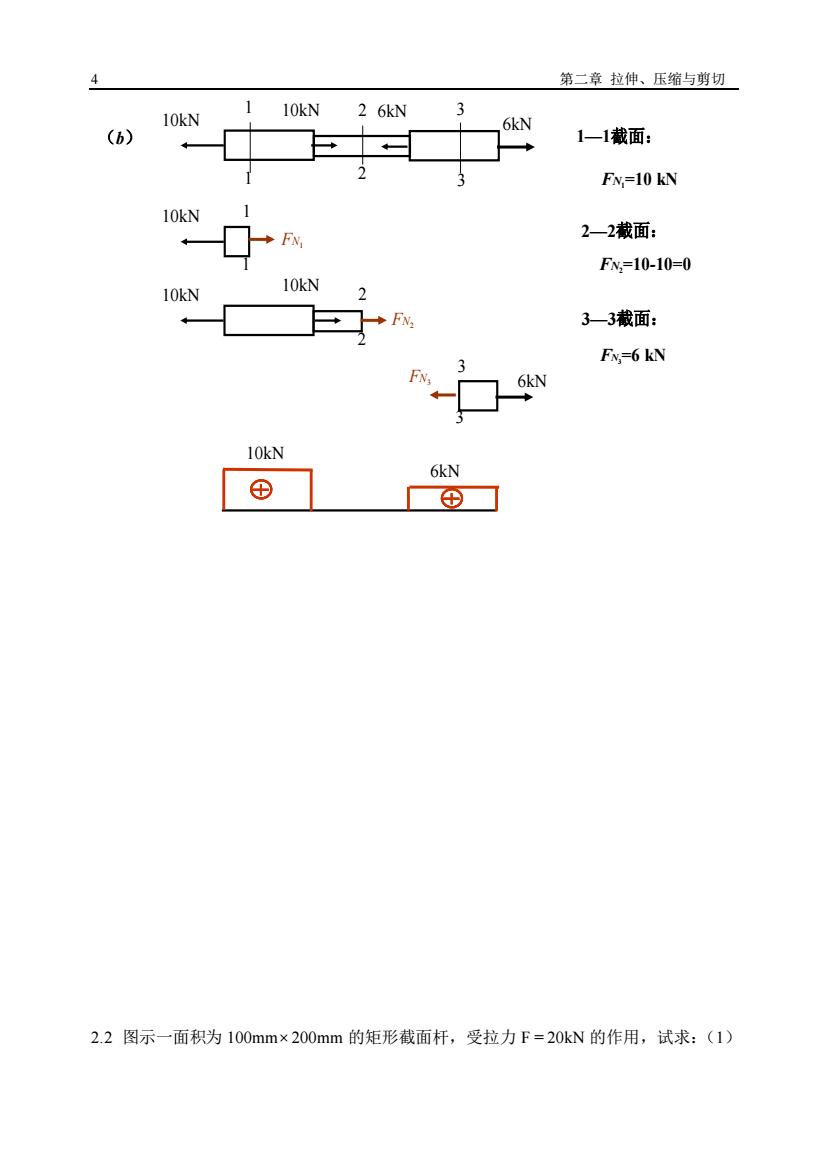
4 第二章 拉伸、压缩与剪切 (b) 10kN 10kN 6kN 6kN 3 3 2 2 1 1 10kN 6kN FN1=10 kN FN2=10-10=0 FN3=6 kN 1—1截面: 2—2截面: 3—3截面: 10kN FN1 1 1 10kN 10kN 2 2 FN2 6kN 3 3 FN3 2.2 图示一面积为 100mm 200mm 的矩形截面杆,受拉力 F = 20kN 的作用,试求:(1)

第二章 拉伸、压缩与剪切0=的斜截面m-m上的应力:(2)最大正应力αm和最大剪应力tm的大小及其作用面的方位角。解:F_ 20×103=1MPaF:A0.1x0.2m3=0.75MPa030°=0cos~α=1x1x%sin60°==0.433MPaT30°2Omax==1MPa=0.5MPaTmax22.3图示一正方形截面的阶梯形混凝土柱。设重力加速度g=9.8m/s混凝土的密度为p=2.04x10°kg/m2,F=100kN,许用应力[0]=2MPa。试根据强度条件选择截面宽度a和b
第二章 拉伸、压缩与剪切 5 6 = 的斜截面 m-m 上的应力;(2)最大正应力 max 和最大剪应力 max 的大小及其作用 面的方位角。 F F m m 解: 3 20 10 1MPa 0.1 0.2 P A = = = 2 30 3 cos 1 0.75MPa 4 = = = 30 1 3 sin60 0.433MPa 2 2 2 = = = max = =1MPa max 0.5MPa 2 = = F 2.3 图示一正方形截面的阶梯形混凝土柱。设重力加速度 g = 9.8m/s2 , 混凝土的密度为 3 3 = 2.0410 kg / m ,F = 100kN,许用应力 = 2MPa 。试根据强度条件选择截面宽度 a 和 b

第二章 拉伸、压缩与剪切6IFP = 2.04×103 ×9.8 = 2×104 N/m2解:FFv_F+ p.4a?FN/=F+p.4d?,01==[]Aa2回100×103=0.228m≥--210-4×2×10FN2=3.F+p.4a?+p.4b2=3×100×103+2×104×4×0.2282+2×104×4×b2304.16×103FN2=0.398m=398mm≥[a],h>2V2×106_4×2×104h22.4在图示杆系中,AC和BC两杆的材料相同,且抗拉和抗压许用应力相等,同为[o]。BC杆保持水平,长度为I,AC杆的长度可随e角的大小而变。为使杆系使用的材料最省试求夹角的值
6 第二章 拉伸、压缩与剪切 b F 4m 4m F F a b F 4m 4m F F a 解: 2 1 N P a = + 4 ,3 4 2 = = 2.04 10 9.8 2 10 N/m 2 1 1 2 1 4 [ ] N P a A a + = = = 3 6 4 100 10 0.228m [ ] 4 2 10 4 2 10 P a = = − − 2 2 2 3 4 2 4 2 3 4 4 3 100 10 2 10 4 0.228 2 10 4 N P a b b = + + = + + 2 2 2 [ ] , N b = 3 6 4 304.16 10 0.398m 398mm 2 10 4 2 10 b = = − FN1 FN1 FN2 FN2 F F F F 2.4 在图示杆系中,AC 和 BC 两杆的材料相同,且抗拉和抗压许用应力相等,同为 。 BC 杆保持水平,长度为 l,AC 杆的长度可随 角的大小而变。为使杆系使用的材料最省, 试求夹角 的值

第二章拉伸、压缩与剪切解KZF,=0,Fn2sn0-F=0,FN2sin ecOsOZF=0Fac0-Fm=0,FFN2FNI1cosoFA2 =A[o][]sino[o][o]sinoA,1Fl1cosO+A1=V=V+V, -cosesincosesinFl(tan 0+2 cot 0)[o]_ sin 0+ cos? 01= tanθ+ cot0)(sin 0cos0sincoso由=0,(tan 0 =-1,(ctg0)=-sindecos?0d12(tan 0+2ctg0) ==0decos"のsin"?sin?0-2cos?0=0,sin?0-2cos?0=0sin?0cos?0tan?0=2, tan0= V2,0= 54.44°
第二章 拉伸、压缩与剪切 7 F FN2 FN1 C F FN2 FN1 C F sin 0 , sin 0 , 2 2 F FY = FN − F = FN = FX FN FN FN F sin cos 0 , cos 0 , 2 1 1 = − = = 1 1 1 , sin N A P = = 2 2 cos sin N A P = = FN2 FN1 A2 F A1 F 解: ) sin cos sin cos 1 ( cos 1 2 1 2 = + = + = + Fl Al A l V V V (tan 2cot) = + Fl tan cot ) sin cos sin cos sin cos 1 ( 2 2 = + + = 2 2 sin 1 , ( ) cos 1 0 ,(tan ) − = = ctg = d d 由 V 0 sin 2 cos 1 (tan 2 ) 2 2 + = − = ctg d d 0 ,sin 2cos 0 sin cos sin 2cos 2 2 2 2 2 2 = − = − 54.44 tan 2 , tan 2 , 2 = = =