
8.2.已知应力状态如图所示,应力单位为MPa。试用解析法和应力圆分别求:(1)主应力大小,主平面位置;(2)在单元体上绘出主平面位置及主应力方向:(3)最大切应力。2080430(e)解: (b)(1)应力分量,=50MPa ,=0=-20MPa主平面位置和主应力大小2t.=0.8tg2αga,-,.%=19.3°α+90°=109.3°fomax_a,+a,or-ory+tCJ57.0 MPa-+/g(-20 -{-7.0 MPa..0, = 57.0 MPa, =-7.0 MPa=(2)画主平面位置及主应力方向:>0y,α0面对应0ma1019(3)最大剪应力_g-0;_ 570+70 =32.0MPa(4)应力圆
8.2. 已知应力状态如图所示,应力单位为 MPa。试用解析法和应力圆分别求:(1)主应力大 小,主平面位置;(2)在单元体上绘出主平面位置及主应力方向;(3)最大切应力。 20 80 (e) 20 30 (f) 20 20 50 (b) 40 40 (d) 20 解:(b) (1) 应力分量 50 0 20 σ x yx = == MPa σ τ y − MPa 主平面位置和主应力大小 0 0 0 2 2 0.8 19.3 90 109.3 xy x y o o tg τ α σ σ α α =− = − o ∴ = += max 2 2 min 2 2 1 2 3 ( ) 2 2 50 50 57.0 ( ) ( 20) 2 2 7.0 57.0 0 7.0 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ ⎧ = ± +− = ⎨ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向: σx>σy,α0面对应σmax。 19.3o σ3 σ1 (3) 最大剪应力 1 3 max 57.0 7.0 32.0 2 2 MPa σ σ τ − + == = (4) 应力圆 (50,-20) (0, 20) 38.6o -7.0 57.0 σ τ

(d) (1)应力分量O,=-40 MPa ,=-20MPa y=-40MPa主平面位置和主应力大小27gtg2αg=a,-0,α + 90°= 52'.α,=-38°o,+o,amax0+tgmin2) +(-40)°- 1.2 MPa-40+20)-20{-71.2 MPa2.. 0, =11.2 MPa0, =-71.2 MPa0=U(2)画主平面位置及主应力方向:α<0y,αo面对应omin(3)最大剪应力_11.2+71.2=41.2MPa(4)应力圆(e)(1)应力分量,=0,=-80MPa T,=20MPa主平面位置和主应力大小27tg2αg-0.5a,-a,.. α = -13.3°α + 90°= 76.7°上海理工大学力学教研室
(d) (1) 应力分量 40 20 40 σ x yx = − MPa σ τ = − MPa y = − MPa 主平面位置和主应力大小 0 0 0 2 2 4 38 90 52 xy x y o o tg τ α σ σ α α =− =− − o ∴ =− + = ( ) 2 max 2 min 2 2 1 2 3 2 2 40 20 40 20 11.2 40 2 2 71.2 11.2 0 71.2 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎛ ⎞ ⎨ =± + ⎜ ⎟ ⎩ ⎝ ⎠ −− −+ ⎛ ⎞ ⎧ = ± +− = ⎜ ⎟ ⎨ ⎝ ⎠ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向: σx<σy,α0面对应σmin。 38o σ3 σ1 (3) 最大剪应力 1 3 max 11.2 71.2 41.2 2 2 MPa σ σ τ − + == = (4) 应力圆 (-40,-40) (-20,40) 76o -71.2 11.2 σ τ (e) (1) 应力分量 0 80 20 σ x y = =− = σ τ MPa MPa xy 主平面位置和主应力大小 0 0 0 2 2 0. 13.3 90 76.7 xy x y o o tg 5 o τ α σ σ α α =− =− − ∴ =− + = 上海理工大学 力学教研室 1

max_o,+,+gr-a,y+tT.-+2-17m{-84.7MPa..a,=4.7MPa 0,=0g,=-84.7MPa(2)画主平面位置及主应力方向:a>0,αo面对应omax。/o(3)最大剪应力4.7+84.7=44.7MPa(4)应力圆(f)(1)应力分量,=30MPa t,=20MPao,=-20MPa主平面位置和主应力大小2g=0.8tg2αg=O,-0,.α%=19.3°α +90°=109.3°fomax_a, +o,.o.-o,y+tgmin[37MPa20+30-20 - 30 +20° ={-27MPa2..0, = 37MPa,=0 ,=-27MPa(2)画主平面位置及主应力方向:oKc,o0面对应0mmn。上海理工大学力学教研室
max 2 2 min 2 2 1 23 ( ) 2 2 80 80 4.7 ( ) 20 2 2 84.7 4.7 0 84.7 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ − ⎧ = ± += ⎨ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向: σx>σy,α0面对应σmax。 13.3o σ3 σ1 (3) 最大剪应力 1 3 max 4.7 84.7 44.7 2 2 MPa σ σ τ − + == = (4) 应力圆 (0,20) (-80,-20) 26.6o -84.7 4.7 σ τ (f) (1) 应力分量 20 30 20 σ x yx = − MPa MPa MPa σ τ = y = 主平面位置和主应力大小 0 0 0 2 2 0.8 19.3 90 109.3 xy x y o o tg o τ α σ σ α α =− = − ∴= + = max 2 2 min 2 2 1 23 ( ) 2 2 20 30 20 30 37 ( ) 20 2 2 27 37 0 27 xy xy xy MPa MPa MPa MPa σ σσ σσ τ σ σ σσ ⎧ + − ⎨ =± + ⎩ −+ −− ⎧ = ± += ⎨ ⎩− ∴ = = =− (2) 画主平面位置及主应力方向:σx<σy,α0面对应σmin。 上海理工大学 力学教研室 2
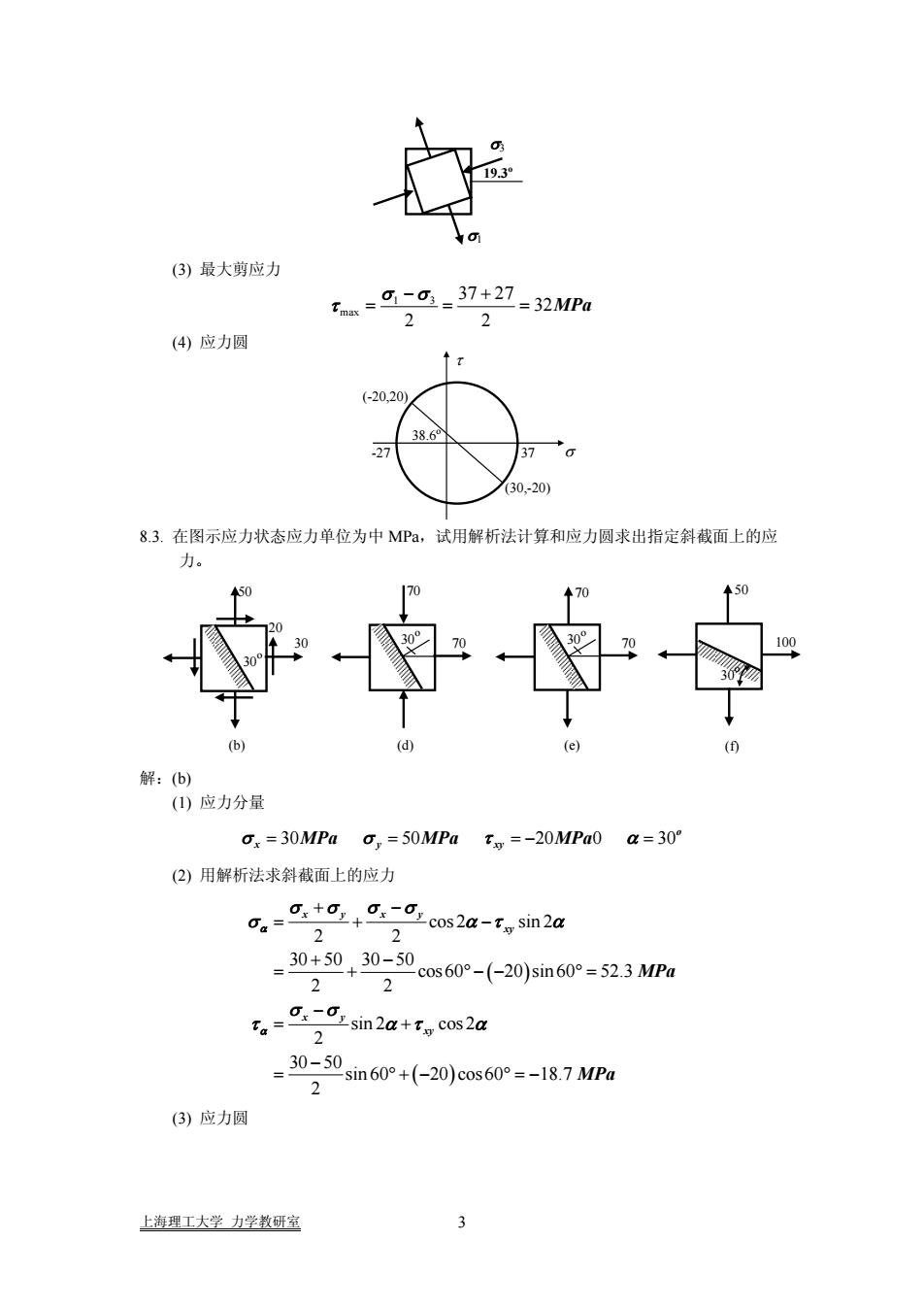
(3)最大剪应力37+2732MPa(4) 应力圆208.3.在图示应力状态应力单位为中MPa,试用解析法计算和应力圆求出指定斜截面上的应力0(d)(e)(f)解:(b)(1)应力分量o,=30MPa,=50MPaTm=-20MPa0α=30°(2)用解析法求斜截面上的应力+cos2α-ty sin2a. =30+50,3050cos60°-(-20)sin 60°= 52.3 MPa-0Isin2α+Tg cos2α30-50sin 60°+(-20)cos60°= -18.7 MPa(3)应力圆上海理工大学力学教研室
19.3o σ3 σ1 (3) 最大剪应力 1 3 max 37 27 32 2 2 MPa σ σ τ − + === (4) 应力圆 (30,-20) (-20,20) 38.6o -27 37 σ τ 8.3. 在图示应力状态应力单位为中 MPa,试用解析法计算和应力圆求出指定斜截面上的应 力。 70 70 (d) 30o 50 100 (f) 30o 70 70 (e) 30o 30 50 (b) 30o 20 解:(b) (1) 应力分量 30 50 20 0 30o σστ α x yx === MPa MPa y − MPa = (2) 用解析法求斜截面上的应力 ( ) ( ) cos 2 sin 2 2 2 30 50 30 50 cos 60 20 sin 60 52.3 2 2 sin 2 cos 2 2 30 50 sin 60 20 cos60 18.7 2 xy xy xy x y xy MPa MPa α α σ σ σσ σ α τ α σ σ τ α τ α + − =+ − + − = + °− − °= − = + − = ° + − ° = − (3) 应力圆 上海理工大学 力学教研室 3

30.-20(d)(1)应力分量0,=70MPa ,=-70MPag=0α=30°(2)用解析法求斜截面上的应力o2a-ysin2a7000+70cos60=35MPa-arsin2α+cos2a70 + 70sin 60°= 60.6MPa(3)应力圆(e)(1)应力分量,=70MPa,=70MPaT,=0α=30°(2)用解析法求斜截面上的应力o, +o,o-0-cos2a -t , sin 2a6._70 +70=70MPa0-0sin 2a +t , cos2a = 0(3)应力圆:为一点圆(70,0)上海理工大学力学教研室
60o σ τ (30,-20) (50, 20) (52.3, -18.7) (d) (1) 应力分量 70 70 0 30o σ σ τα xy x = = MPa − = MPa y = (2) 用解析法求斜截面上的应力 cos 2 sin 2 2 2 70 70 70 70 cos60 35 2 2 sin 2 cos2 2 70 70 sin 60 60.6 2 xy xy xy x y xy MPa MPa α α σ σ σσ σ ατ α σ σ τ α τ α + − =+ − − + = + °= − = + + = ° = (3) 应力圆 -70 70 (35,60.6) 60o σ τ (e) (1) 应力分量 o σ x = MPa σ y = MPa xy = ατ = 30 0 70 70 (2) 用解析法求斜截面上的应力 02cos2sin 2 70 2 7070 2sin2cos 22 + = − = = + = − − + + = ατα σσ τ ατα σσσσ σ α α x yx x yxyx MPa (3) 应力圆:为一点圆 (70,0) σ τ 上海理工大学 力学教研室 4