5.1.图示结构中,设P、9、a均为已知,截面1-1、2-2、3-3无限接近于截面C或截面D试求截面1-1、2-2、3-3上的剪力和弯矩。P-200NP=qa21131T200 200200O(6)M=qa P=qoq-10kN/mT2D200 + 200 200(d)(c)解: (a)(1)截开1-1截面,取右段,加内力=01Q1MC求内力Q, = P+qa= 2qaM,=-Pxa-qax-59(2)截开2截面,取右段,加内力M=qa-0实M.C求内力Q, = P+ qa=2qaM,=-Pxa-qax+ M=--qa(b) (1)求约束反力P-200NR, 200 200 200RD
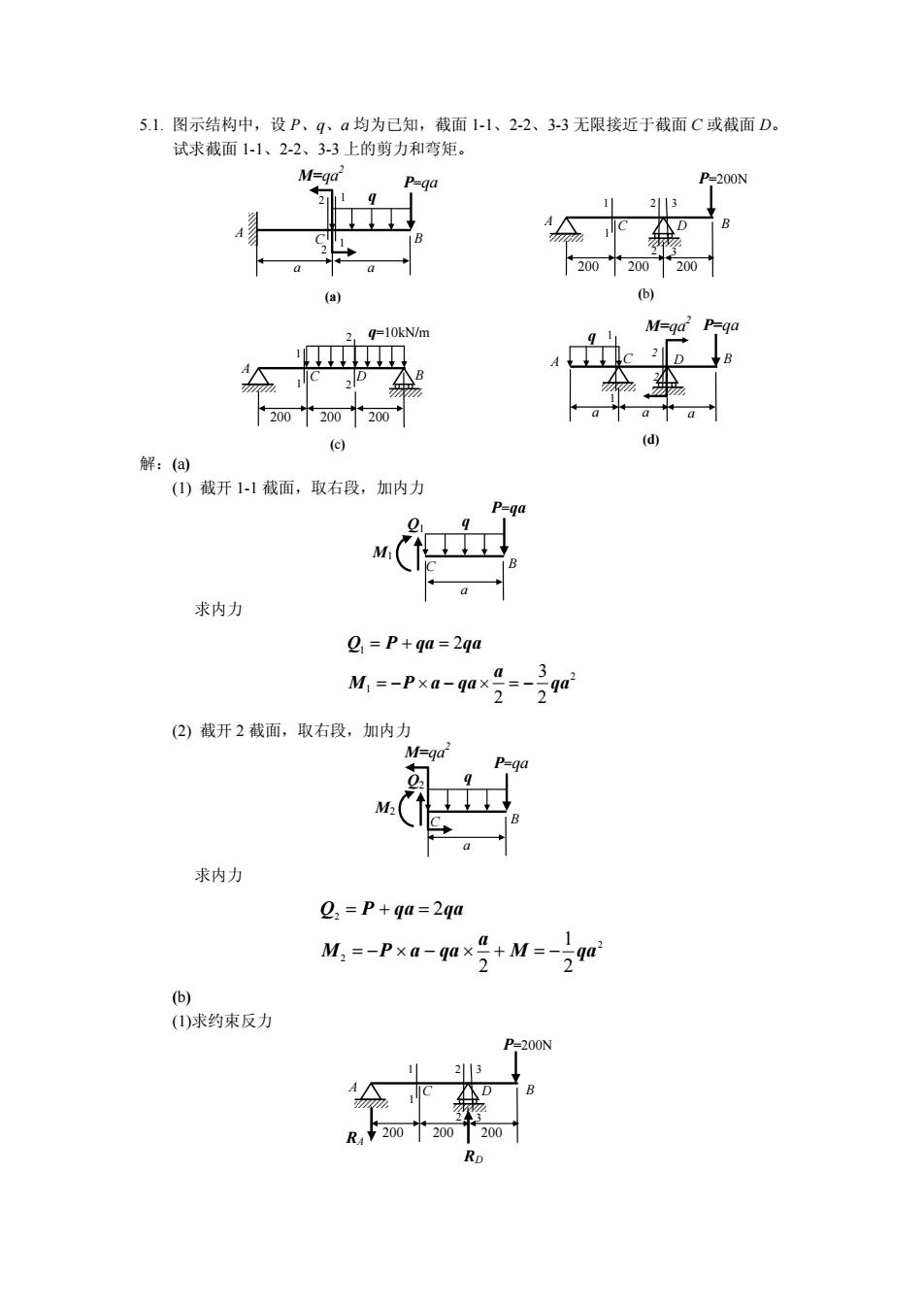
5.1. 图示结构中,设 P、q、a 均为已知,截面 1-1、2-2、3-3 无限接近于截面 C 或截面 D。 试求截面 1-1、2-2、3-3 上的剪力和弯矩。 q (a) a a M P=qa =qa 2 C B A 2 1 1 2 (b) 200 A P=200N 200 200 C D B 1 2 3 2 3 1 (d) A P=qa a q D B 1 2 a a M=qa 2 C 1 2 (c) 200 A q=10kN/m 200 200 C D B 1 2 1 2 解:(a) (1) 截开 1-1 截面,取右段,加内力 Q1 M1 q P=qa B a C 求内力 1 2 1 2 3 2 2 Q P qa qa a M P a qa qa =+ = =− × − × =− (2) 截开 2 截面,取右段,加内力 Q2 M2 q P=qa B a C M=qa 2 求内力 2 2 2 2 1 2 2 qaM a qaaPM qaqaPQ −=+×−×−= += = (b) (1)求约束反力 RD RA 200 A P=200N 200 200 C D B 1 2 3 2 3 1

ZM,=0R,×400-P×200=0R,=100N(2)截开1-1截面,取左段,加内力5aimVRA求内力Q =-R, =-100NM,=-R,x0.2=-20Nm(3)截开2-2截面,取左段,加内力ODDMAVRA求内力Q, =-R, =-100NM,=-R,×0.4=-40Nm(4))截开3-3截面,取右段,加内力P-200NMCF求内力Q,=P=200NM, =-P×0.2=-40Nm(c) =10kN/n(1)求约束反力PARF200200200REZM,=0Rg×0.6-(q×0.4)×0.4=0Re= 2667 NZMg=0-R ×0.6 +(q×0.4)×0.2 =0R, =1333 N(2)截开1-1截面,取左段,加内力01m1AR上海理工大学力学教研室
0 400 200 0 100 D A A MR P R N = × −× = ∑ = m (2) 截开 1-1 截面,取左段,加内力 A C RA Q1 M1 求内力 1 1 100 0.2 20 A A QR N MR N = − =− =− × =− (3) 截开 2-2 截面,取左段,加内力 A D RA Q2 M2 求内力 2 2 100 0.4 40 A A QR N MR Nm = − =− =− × =− (4) 截开 3-3 截面,取右段,加内力 P=200N M3 D B Q3 求内力 3 2 200 0.2 40 QP N MP Nm = = =− × =− (c) 200 A q=10kN/m 200 200 C D B 1 2 1 2 RA RB (1) 求约束反力 ( ) ( ) 0 0.6 0.4 0.4 0 2667 0 0.6 0.4 0.2 0 1333 A B B B A A MR q R N M Rq R N = × −× × = = = − × +× × = = ∑ ∑ (2) 截开 1-1 截面,取左段,加内力 上海理工大学 力学教研室 1 A C B AB Q1 M1 R

求内力Q = R, = 1333 NM,=R,×0.2=266.6N.m(3)截开2-2截面,取右段,加内力91-10kN/mMCQ, =-Rg +q×0.2 =-0.667 NM, = Rs ×0.2 -(q×0.2)×0.1= 333.4 N.m(d)(1)求约束反力M=g P-qa李兴aRcRpZM,=0 Rexa+qxax1.5a-M-Pxa=0Re=-qa(2)截开1-1截面,取左段,加内力OM求内力Q=-qa M,=-qax(3)截开2-2截面,取左段,加内力求内力RQ, =-qa-Rc =-号qaM, =-Rc ×a-(qxa)x1.5a=-2qa25.3.设图示各梁的载荷P、q、m和尺寸a皆为已知。(1)列出梁的剪力方程和弯矩方程(a、b)(2)作剪力图和弯矩图;(3)判定lQlmax和|Mlmax2上海理工大学力学教研室
求内力 1 1 1333 0.2 266.6 . A A QR N M R Nm = = =×= (3) 截开 2-2 截面,取右段,加内力 q=10kN/m D B RB M2 Q2 ( ) 2 2 0.2 0.667 0.2 0.2 0.1 333.4 . B B Q Rq N MR q N m =− + × =− = × −× × = (d) (1) 求约束反力 A P=qa a q D B 1 2 a a M=qa 2 C 1 2 RC RD 0 1.5 0 1 2 D C C M R aqa a M Pa R qa = ×+×× − − × = ∑ = (2) 截开 1-1 截面,取左段,加内力 A q C Q1 M1 求内力 2 1 1 1 1 2 2 Q qa M qa a qa =− =− × =− (3) 截开 2-2 截面,取左段,加内力 A q C Q2 M2 D 求内力 RC ( ) 2 2 2 3 2 1.5 2 C C Q qa R qa M R a qa a q =− − =− =− × − × × =− a 5.3. 设图示各梁的载荷P、q、m和尺寸a皆为已知。(1)列出梁的剪力方程和弯矩方程(a、b); (2)作剪力图和弯矩图;(3)判定⏐Q⏐max和⏐M⏐max。 上海理工大学 力学教研室 2
Mo=P(b)2(d)LGA(0)4-30kN/mP-pN 0NmCADIAEa/2In11m/1m1m(g) 解:(a)(1)求约束反力M,=PZY=0 R,-2P=0R,=2PZM,=0 M,-2Pa+M。=0M, = Pa(2)列剪力方程和弯矩方程(=R,=2P xe(0,a)Q(x)){=R,-2P=0 xe(a,2a)上海理工大学力学教研室
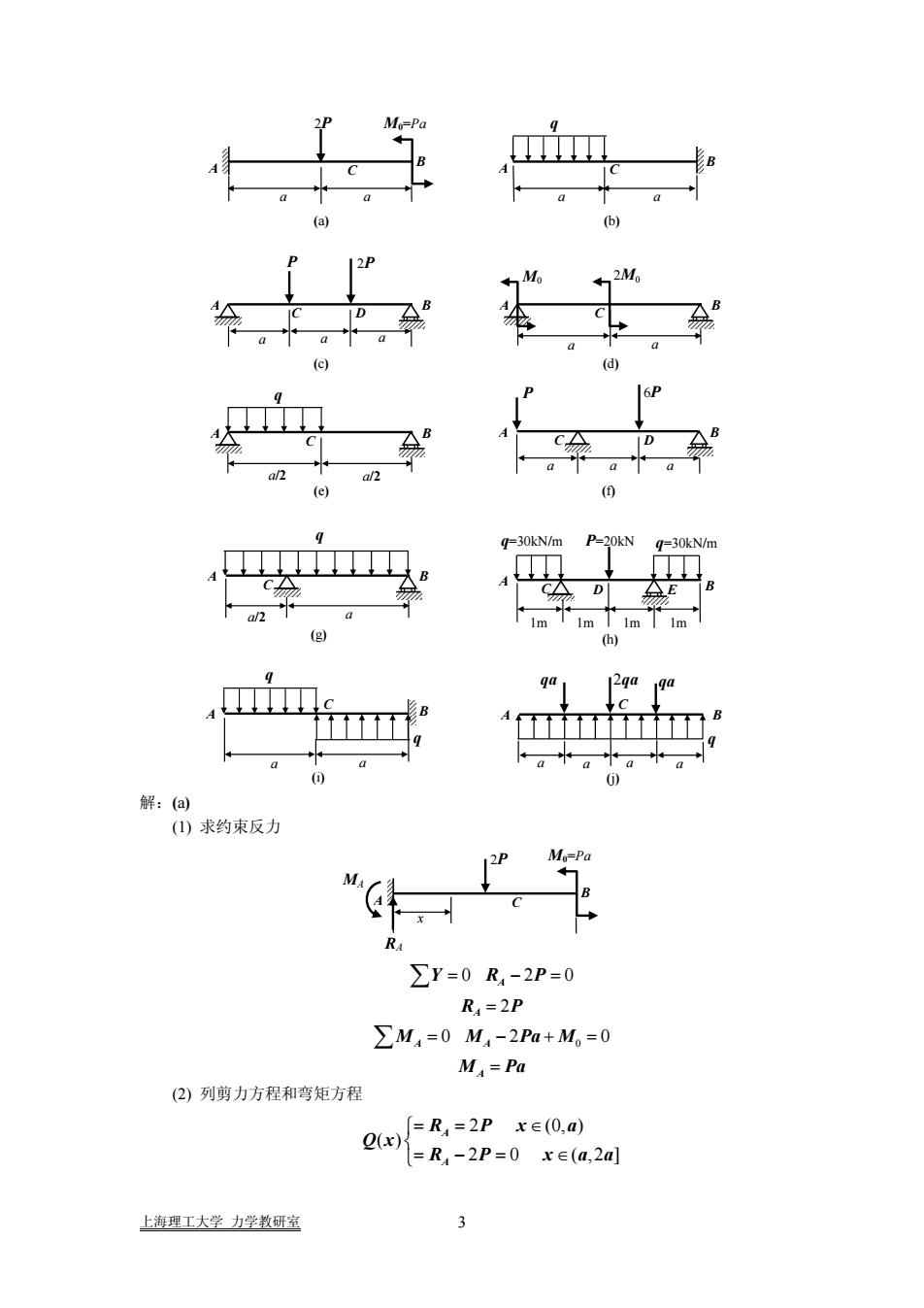
(a) a a 2P M0=Pa C B A (b) a a C B A q (c) a a P C A B a 2P D (d) a a 2M0 C A B M0 (f) a a P C A B a 6P D (e) a/2 a/2 C A B q (g) a/2 C A B a q (h) 1m C B A q=30kN/m P=20kN q=30kN/m 1m 1m 1m D E (i) C A B q q a a (j) C A B qa q a a a a 2qa qa 解:(a) (1) 求约束反力 x 2P M0=Pa C B A RA MA 0 0 2 0 2 0 2 0 A A A A A Y RP R P M M Pa M M Pa = −= = = − += = ∑ ∑ (2) 列剪力方程和弯矩方程 2 (0, ) ( ) 2 0 ( ,2 ] A A R Px a Q x R P x aa ⎧== ∈ ⎨ ⎩=−= ∈ 上海理工大学 力学教研室 3
[=R, ×x+M, =2Px- Paxe(0,a)M(x)[=R xx+M -2Px(x-a)=Pa xe[0,a)(3)画Q图和M图EL(4)最大剪力和最大弯矩值[0 =2P [Mm| =- Pa(b) (1)求约束反力B)MZ=0 Rg-qa=0Rg= qaZM,=0 -M,+qax1.5a=0M=jqd(2)列剪力方程和弯矩方程-qxxe[0,a]0(x)-qaxe[a,2a]xe[0,a]M(x)-qax(x-)xe[a,2a](3)画Q图和M图2上海理工大学力学教研室
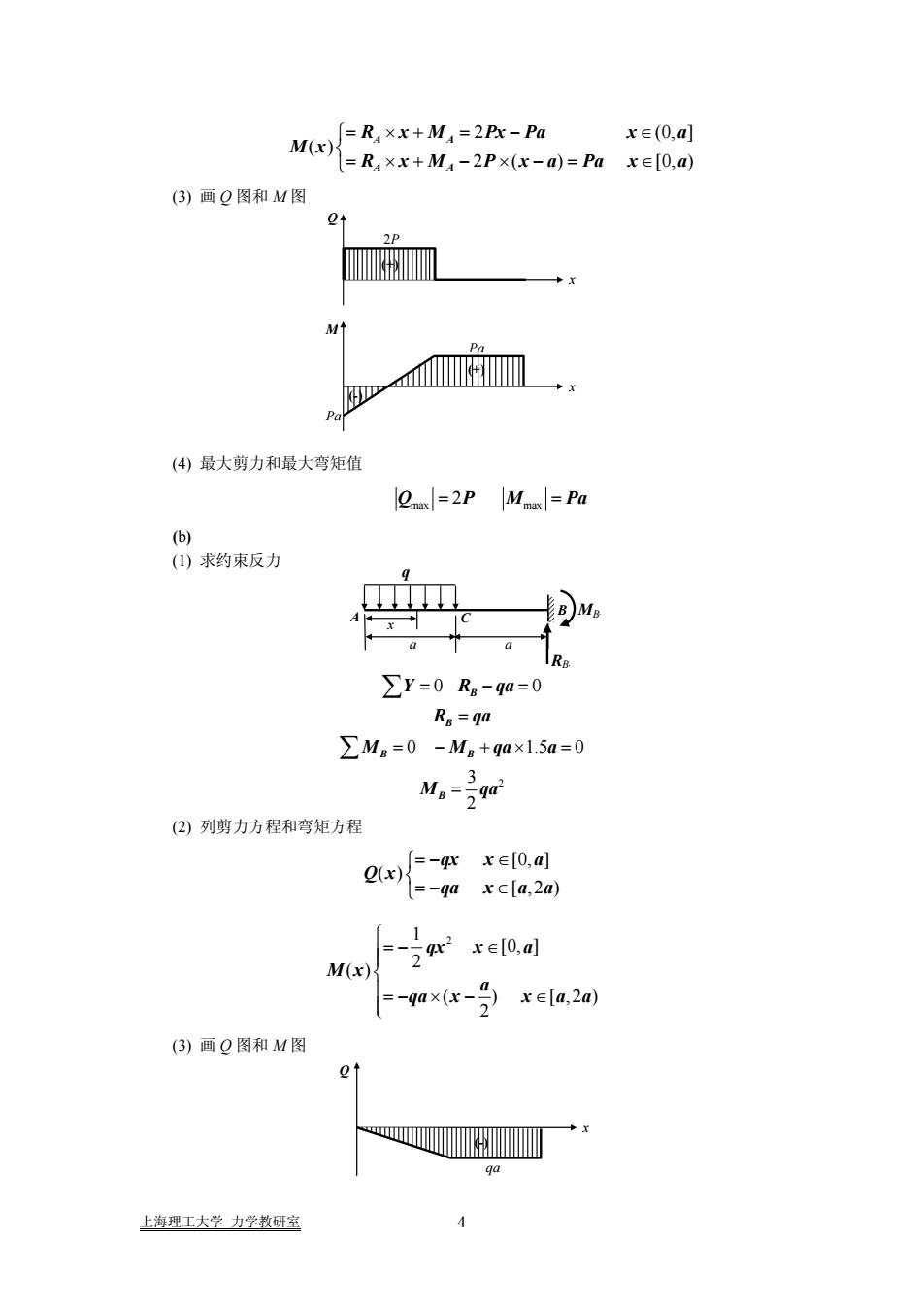
2 (0, ] ( ) 2 ( ) [0, ) A A A A R x M Px Pa x a M x R x M P x a Pa x a ⎧= ×+ = − ∈ ⎨ ⎩= ×+ − × − = ∈ (3) 画 Q 图和 M 图 x Q 2P (+) x M Pa (+) (-) Pa (4) 最大剪力和最大弯矩值 max max Q PM = 2 = Pa (b) (1) 求约束反力 q 2 0 0 0 1.5 0 3 2 B B B B B Y R qa R qa M M qa a M qa = −= = = − +× = = ∑ ∑ (2) 列剪力方程和弯矩方程 [0, ] ( ) [ ,2 ) qx x a Q x qa x a a ⎧=− ∈ ⎨ ⎩=− ∈ 1 2 [0, ] 2 ( ) ( ) [ ,2 ) 2 qx x a M x a qa x x a a ⎧ =− ∈ ⎪⎪ ⎨ ⎪=− × − ∈ ⎪⎩ (3) 画 Q 图和 M 图 x Q (-) qa MBB a a B A C x RBB 上海理工大学 力学教研室 4