
fx)、g(x)是P中两个多项式,P是包含P的一个较大的数域。当然f(x)、g(x)也可以 看成P中的多项式。从带余除法可以看出不论把f(x)、g(x)看成是P中或是P中的多 项式,用g(x)去除f(x)所得的商式及余式都是一样的。因此,如果P中g(x)不能整除f(x), 那么在x中,g(x)也不能整除∫(x) 第四节最大公因式 如果多项式(x)既是(x)的因式,又是g(x)的因式,那么p(x)就称为g(x)与f(x)的 个公因式。在公因式中占有特殊重要地位的是所谓最大公因式。 定义6设f(x),g(x)是Px中两个多项式。P]中多项式d(x)称为f(x),(x)的一个 最大公因式,如果它满足下面两个条件: 1)d(x)是f),g(x)的公因式: 2)f(x),g(x)的公因式全是d(x)的因式。 例如,对于任意多项式∫(x),f(x)就是(x)与0的一个最大公因式。特别地,根据定义, 两个零多项式的最大公因式就是0。 等大公因武的游在性的证明主要根据带余障法,关于带会除法我们脂出以下事实如果有 f(x)=q(x)g(x)+r(x) 成立,那么fx),g(x)和g(x),(x)有相同的公因式。事实上,如果(xg(x),p(x(x)。 这就是说,g(x),r(x)的公因式全是f(x),g(x)的公因式。反过来,如果(xg(x,p(xf(x) 那么p(x)一定整除它们的组合 r(x)=f(x)-q(x)g(x) 这就是说,p(x)是fx),g(x)的公因式。由此可见,如果g(x),r(x)有一个最大公因式d(x), 那么d(x)也就是f(x),g(x)的一个最大公因式。 定理2对于P中任意两个多项式f(x),g(x),在Px]中存在一个最大公因式d(x), 且d(x)可以表成f(x),g(x)的一个组合,即有P中多项式u(x,(x)使 d(x)=u(x)f(x)+v(x)g(x) (2)
f (x) 、 g(x) 是 Px 中两个多项式, P 是包含 P 的一个较大的数域。当然 f (x) 、 g(x) 也可以 看成 Px 中的多项式。从带余除法可以看出不论把 f (x) 、g(x) 看成是 Px 中或是 Px 中的多 项式,用 g(x) 去除 f (x) 所得的商式及余式都是一样的。因此,如果 Px 中 g(x) 不能整除 f (x) , 那么在 Px 中, g(x) 也不能整除 f (x) 。 第四节 最大公因式 如果多项式 (x) 既是 f (x) 的因式,又是 g(x) 的因式,那么 (x) 就称为 g(x) 与 f (x) 的一 个公因式。在公因式中占有特殊重要地位的是所谓最大公因式。 定义 6 设 f (x) ,g(x) 是 Px 中两个多项式。 Px 中多项式 d (x) 称为 f (x) ,g(x) 的一个 最大公因式,如果它满足下面两个条件: 1) d (x) 是 f (x) , g(x) 的公因式; 2) f (x) , g(x) 的公因式全是 d (x) 的因式。 例如,对于任意多项式 f (x) ,f (x) 就是 f (x) 与 0 的一个最大公因式。特别地,根据定义, 两个零多项式的最大公因式就是 0。 最大公因式的存在性的证明主要根据带余除法,关于带余除法我们指出以下事实:如果有 等式 f (x) = q(x)g(x) + r(x) 成立,那么 f (x) , g(x) 和 g(x),r(x) 有相同的公因式。事实上,如果 (x) g(x),(x) f (x)。 这就是说, g(x),r(x) 的公因式全是 f (x) ,g(x) 的公因式。反过来,如果 (x) g(x),(x) f (x) 那么 (x) 一定整除它们的组合 r(x) = f (x) − q(x)g(x) 这就是说, (x) 是 f (x) ,g(x) 的公因式。由此可见,如果 g(x) ,r(x) 有一个最大公因式 d (x) , 那么 d (x) 也就是 f (x) , g(x) 的一个最大公因式。 定理 2 对于 Px 中任意两个多项式 f (x) , g(x) ,在 Px 中存在一个最大公因式 d (x) , 且 d (x) 可以表成 f (x) , g(x) 的一个组合,即有 Px 中多项式 u(x), v(x) 使 d(x) = u(x) f (x) + v(x)g(x) (2)

证明如果f(x),g(x)有一个为零,如g(x)=0,那么x)就是一个最大公因式,且 fx)=1·fx)+10 再看一般的情形。不妨设g(x)≠0。按带余除法,用g(x)除∫(x),得到商q,(x),余式(x): 如果(x)≠0,就再用r(x)除g(x),得到商(x),余式5():如果(x)≠0,就再用() 除r(x),得到商q,(x),余式(x):如此辗转相除下去,显然,所得余式的次数不断降低 即 g(x》>(x)0>,(x》>… 因此在有限次之后,必然有余式为零。于是我们有一串等式: f(x)=q(x)g(x)+r(x) g(x)=92(x)r(x)+5(x) t+0t+t00t+。0t0t0+++++0tt+0++00++ r-2(x)=g,(x)r(x)+r(x) … r-3(x)=q-(x)+r-(x) r-2(x)=9(xr-(x)+r.(x) r(x)=9(xr)r(x)+0 ,(x)与0的最大公因式是r,(x)。根据前面的说明,5(x)也就是r(x)与r-(x)的一个最大 公因式:同样的理由不,逐步推上去,r,(x)就是f(x),g(x)的一个最大公因式。 由上面等式容易得到等式 r(x)=u(x)f(x)+v(x)g(x) 这就是定理中的(2)式。 有最大公因式的定义不难看出,如果d,(x,d,(x)是f(x)与g(x)的两个最大公因式,那么 一定有d,(x4,(x)与d4,(xd,(x),也就是d,(x)=cd,(x,c≠0。这就是说,两个多项式的最大 公因式在可以相差一个非零常数倍的意义下是唯一确定的。两个不全为零的多项式的最大公 因式总是一个非零多项式。我们约定月 (fx),gx》 来表示首项系数是1的那个最大公因式。 定理证明中用来求最大公因式的方法通常称为辗转相除法
证明 如果 f (x) , g(x) 有一个为零,如 g(x) = 0 ,那么 f (x) 就是一个最大公因式,且 f (x) = 1 f (x) +1 0 再看一般的情形。不妨设 g(x) 0 。按带余除法,用 g(x) 除 f (x) ,得到商 ( ) 1 q x ,余式 ( ) 1 r x ; 如果 r1 (x) 0 ,就再用 ( ) 1 r x 除 g(x) ,得到商 ( ) 2 q x ,余式 ( ) 2 r x ;如果 r2 (x) 0 ,就再用 ( ) 2 r x 除 ( ) 1 r x ,得到商 ( ) 3 q x ,余式 ( ) 3 r x ;如此辗转相除下去,显然,所得余式的次数不断降低, 即 (g(x)) (r1 (x)0 (r2 (x)) 因此在有限次之后,必然有余式为零。于是我们有一串等式: ( ) ( ) ( ) ( ) 1 1 f x = q x g x + r x ( ) ( ) ( ) ( ) 2 1 2 g x = q x r x + r x ………………………………… ( ) ( ) ( ) ( ) 2 1 r x q x r x r x i− = i i− + i ………………………………… ( ) ( ) ( ) 3 1 1 r x q x r x s− = s− + s− ( ) ( ) ( ) ( ) 2 1 r x q x r x r x s− = s s− + s rs−1 (x) = qs+1 (x)rs (x) + 0 r (x) s 与 0 的最大公因式是 r (x) s 。根据前面的说明, r (x) s 也就是 r (x) s 与 ( ) 1 r x s− 的一个最大 公因式;同样的理由不,逐步推上去, r (x) s 就是 f (x) , g(x) 的一个最大公因式。 由上面等式容易得到等式 r (x) u(x) f (x) v(x)g(x) s = + 这就是定理中的(2)式。 有最大公因式的定义不难看出,如果 ( ), ( ) 1 2 d x d x 是 f (x) 与 g(x) 的两个最大公因式,那么 一定有 ( ) ( ) 1 2 d x d x 与 ( ) ( ) 2 1 d x d x ,也就是 d1 (x) = cd2 (x),c 0 。这就是说,两个多项式的最大 公因式在可以相差一个非零常数倍的意义下是唯一确定的。两个不全为零的多项式的最大公 因式总是一个非零多项式。我们约定用 ( f (x), g(x)) 来表示首项系数是 1 的那个最大公因式。 定理证明中用来求最大公因式的方法通常称为辗转相除法
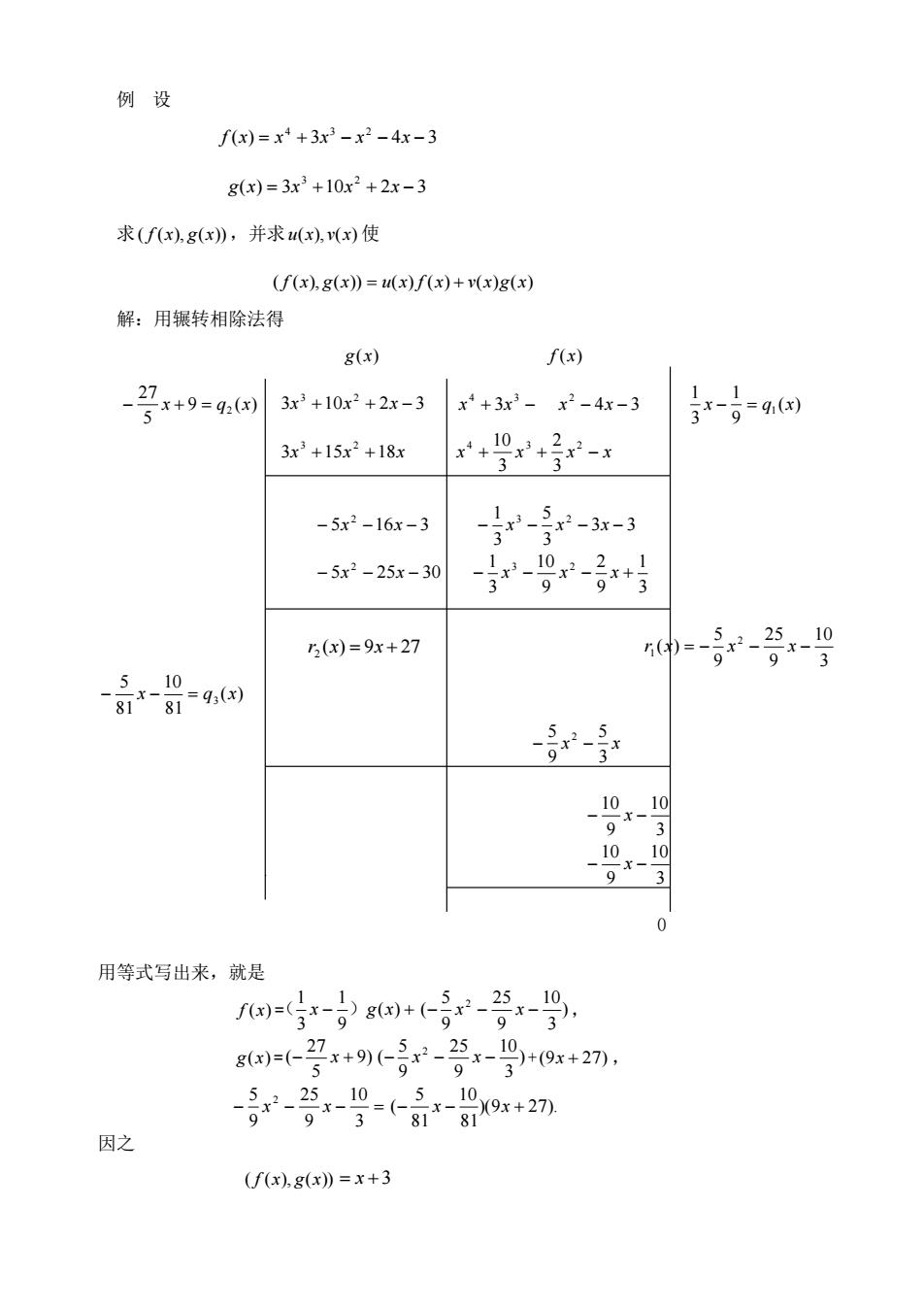
例设 f(x)=x+3x3-x2-4x-3 g(x)=3x3+10x2+2x-3 求(fx),g(x),并求u(x,Mx)使 (f(x),g(x》=(x)f(x)+(x)g(x) 解:用辗转相除法得 g(x) f(x) 27 x+9=9) 3x3+10x2+2x-3x+3x3-x2-4x-3 3x3+15x2+18x +9+号-x 3 -5.x2-16x-3 r--3-3 -5x2-25x-30 9 5(x)=9x+27 --9 -2-x 0 用等式写出来,就是 --号g+3--9. 8=-2+9-x-9-9x+2 因之 (fxgx》=x+3
例 设 ( ) 3 4 3 4 3 2 f x = x + x − x − x − ( ) 3 10 2 3 3 2 g x = x + x + x − 求 ( f (x), g(x)) ,并求 u(x), v(x) 使 ( f (x), g(x)) = u(x) f (x) + v(x)g(x) 解:用辗转相除法得 g(x) f (x) 9 ( ) 5 27 2 − x + = q x 3 10 2 3 3 2 x + x + x − 3 4 3 4 3 2 x + x − x − x − ( ) 9 1 3 1 1 x − = q x 3x 15x 18x 3 2 + + x + x + x − x 4 3 2 3 2 3 10 5 16 3 2 − x − x − 3 3 3 5 3 1 3 2 − x − x − x − 5 25 30 2 − x − x − 3 1 9 2 9 10 3 1 3 2 − x − x − x + r2 (x) = 9x + 27 3 10 9 25 9 5 ( ) 2 r1 x = − x − x − ( ) 81 10 81 5 3 − x − = q x x x 3 5 9 5 2 − − 3 10 9 10 − x − 3 10 9 10 − x − 0 用等式写出来,就是 f (x) = − ( ) + 9 1 3 1 ( x )g x ) 3 10 9 25 9 5 ( 2 − x − x − , g(x) = 9) 5 27 (− x + ) 3 10 9 25 9 5 ( 2 − x − x − + (9x + 27) , − − − = 3 10 9 25 9 5 2 x x )(9 27). 81 10 81 5 (− x − x + 因之 ( f (x), g(x)) = x + 3

而 9x+2-8-2+9--9 =g-马+[a-(令g 号-r+1-g--a =号-+号+ 于是 auwω得x-ym+(传+号t国 定义7Px中两个多项式f(x),g(x)称为互素的,如果(f(x),g(x》=1。 显然,如果两个多项式互素,那么它们除去零次多项式外没有其他的公因式,反之亦然。 定理3P中两个多项式fx),gx)互素的充分必要条件是有P)中的多项式(x),(x)使 u(x)f(x)+v(x)g(x)=1 证明必要条件是定理2的直接推论。 现在设有(x),r(x)使 u(x)f(x)+v(x)g(x)=1 而o(x)是f(x)与g(x)的一个最大公因式。于是p(xf(x),p(xg(x),从而p(x儿,即f(x), g(x)互素。 定理4如果(f(x),g(x》=l,且fxg(x)hx),那么f(xh)。 证明由((x),g(x》=1可知,有(x),(x)使 4(x)f(x)+v(x)gr)=1, 等式两边乘h(x),得 u(x)f(x)h(x)+v(x)g(x)h(x)=h(x) 因为f(xg(x)hx),所以f(x)整除等式左端,从而 f(x)h(x). 推论如果(xg(x,f(xg(x),且(f(x,(x》=1,那么f(x)f(xg(x)
而 (9x + 27) = g(x) − 9) 5 27 (− x + ) 3 10 9 25 9 5 ( 2 − x − x − = g(x) − 9) 5 27 (− x + f (x)- ( ) 9 1 3 1 ( x − )g x = ( ) 9 1 3 1 9 5 27 9) ( ) 1 5 27 ( x f x x x g x − − + − − = ( ) 5 18 5 9 9) ( ) 5 27 ( 2 x f x x xg x − + − + 于是 ( f (x), g(x)) = ( ) 5 2 5 1 1 ( ) 5 3 2 x f x x xg x + − + − 定义 7 Px 中两个多项式 f (x) , g(x) 称为互素的,如果 ( f (x), g(x)) =1。 显然,如果两个多项式互素,那么它们除去零次多项式外没有其他的公因式,反之亦然。 定理 3 Px 中两个多项式 f (x) ,g(x) 互素的充分必要条件是有 Px 中的多项式 u(x), v(x) 使 u(x) f (x) + v(x)g(x) = 1 证明 必要条件是定理 2 的直接推论。 现在设有 u(x), v(x) 使 u(x) f (x) + v(x)g(x) = 1 而 (x) 是 f (x) 与 g(x) 的一个最大公因式。于是 (x) f (x),(x) g(x), 从而 (x)1, 即 f (x) , g(x) 互素。 定理 4 如果 ( f (x), g(x)) =1,且 f (x) g(x)h(x), 那么 f (x) h(x)。 证明 由 ( f (x), g(x)) =1 可知,有 u(x), v(x) 使 u(x) f (x) + v(x)g(x) = 1, 等式两边乘 h(x), 得 u(x) f (x)h(x) + v(x)g(x)h(x) = h(x) 因为 f (x) g(x)h(x), 所以 f (x) 整除等式左端,从而 f (x) h(x). 推论 如果 ( ) ( ), 1 f x g x ( ) ( ) 2 f x g x ,且 ( f 1 (x), f 2 (x)) =1 ,那么 ( ) ( ) ( ) 1 2 f x f x g x

证明由(x)g(x)有 g(x)=f(x)h(x). 因为f(xf(x)h(x),且(f(x,f(x》=1,所以根据定理4,有(xh,(x),即 h(x)=f(x)h(x) 代入上式即得 g(x)=f(x)f(x)h(x) 这就是说, f(x)f(xg(x)。 在上面,最大公因式与互素的概念,都是对两个多项式定义的。事实上,对于任意多个多项 式(x),(x,,f,(x(s之2)也同样可以定义最大公因式,dx)称为 f(x),,(x,,∫.(xs≥2)的一个最大公因式,如果d(x)具有下面的性质: 1)dx/(xi=1,2,…s 2)如果xf(x),i=1,2,…,s,那么p(x)d(x)。 我们仍用符号(x),f(x.,f(x)来表示首项系数为1的最大公因式,且存在 4,(x,i=1,2…,s使 4(x)f(x)+42(x)f2(x)+…+4,(x)f(x)=f(x),f2(x,…,f(x) 如果x,2(x,…,(x)=1,那么f(x(x…,(x)就称为互素的。 第五节因式分解定理 选定一个数域P作为系数域,考虑数域P上的多项式环P]中多项式的因式分解。 定义8数域P上次数≥1的多项式(x)称为数域P上的不可约多项式,如果它不能表成数 域P上的两个次数比(x)低的多项式的乘积。 按照定义,一次多项式总是不可约多项式。 如上面指出的,x2+2是实数域上的不可约多项式,但是它在复数域上可以分解成两个一次 多项式的乘积,因而不是不可约多项式。这说明了,一个多项式是否不可约是依赖与系数域 的。 显然,不可约多项式p(x)的因式只有非零常数和它自身的非零常数倍p(xc≠0)这两种
证明 由 ( ) ( ) 1 f x g x 有 ( ) ( ) ( ) 1 1 g x = f x h x 。 因为 ( ) ( ) ( ) 2 1 1 f x f x h x ,且 ( f 1 (x), f 2 (x)) =1 ,所以根据定理 4,有 ( ) ( ) 2 1 f x h x ,即 ( ) ( ) ( ) 1 2 2 h x = f x h x 代入上式即得 ( ) ( ) ( ) ( ) 1 2 2 g x = f x f x h x 这就是说, ( ) ( ) ( ) 1 2 f x f x g x 。 在上面,最大公因式与互素的概念,都是对两个多项式定义的。事实上,对于任意多个多项 式 ( ), ( ), , ( )( 2) f 1 x f 2 x f s x s 也 同 样 可 以 定 义 最 大 公 因 式 , d (x) 称 为 ( ), ( ), , ( )( 2) f 1 x f 2 x f s x s 的一个最大公因式,如果 d (x) 具有下面的性质: 1) d x f x i s i ( ) ( ), =1,2, , 2)如果 (x) f (x),i 1,2, ,s, i = 那么 (x) d(x)。 我们仍用符号 ( ( ), ( ), , ( )) 1 2 f x f x f x s 来表示首项系数为 1 的最大公因式,且存在 u x i s i ( ), =1,2, , 使 u1 (x) f 1 (x) + u2 (x) f 2 (x) ++ us (x) f s (x) = ( ( ), ( ), , ( )) 1 2 f x f x f x s 如果 ( ( ), ( ), , ( )) 1 2 f x f x f x s =1,那么 ( ), ( ), , ( ) 1 2 f x f x f x s 就称为互素的。 第五节 因式分解定理 选定一个数域 P 作为系数域,考虑数域 P 上的多项式环 Px 中多项式的因式分解。 定义 8 数域 P 上次数 1 的多项式 p(x) 称为数域 P 上的不可约多项式,如果它不能表成数 域 P 上的两个次数比 p(x) 低的多项式的乘积。 按照定义,一次多项式总是不可约多项式。 如上面指出的, 2 2 x + 是实数域上的不可约多项式,但是它在复数域上可以分解成两个一次 多项式的乘积,因而不是不可约多项式。这说明了,一个多项式是否不可约是依赖与系数域 的。 显然,不可约多项式 p(x) 的 因式只有非零常数和它自身的非零常数倍 cp(x)(c 0) 这两种