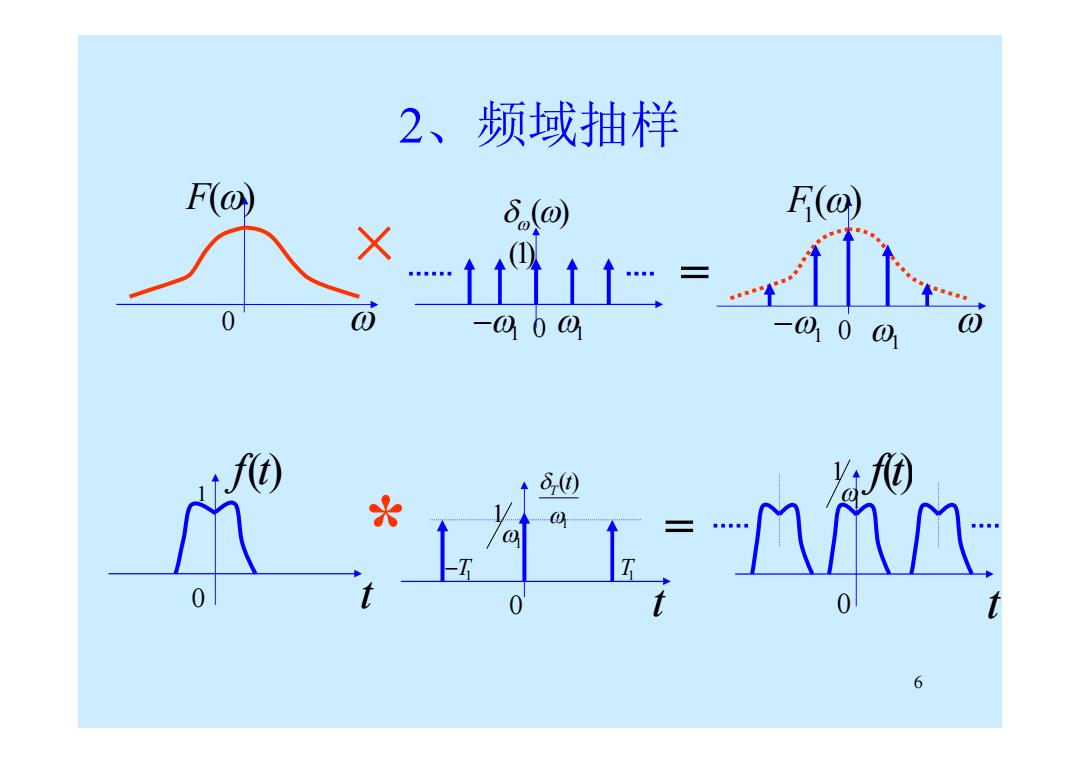
2、频域抽样 F(o) 6(0 (@) 0 -00⊙ -01001 6
6 2、频域抽样 F() 0 f(t) 0 t 1 1 f(t) 0 t 1 1 ( ) t T 1 1 T1 T1 0 t ( ) F1 0 1 0 1 () (1) 1 1 = = × *

§3.9抽样定理sampling theorem (一)时域抽样定理 奈奎斯特定理(Nyquist) 一个频率有限信号f(t)如果频谱只占据-0m→+0m 的范围,则信号∫(t)可以用等间隔的抽样值来唯一地表 示。而抽样间隔T,不大于 2fm 或者说最低抽样频率 为2fm· 奈奎斯特频率: fs=2fm 或 0=20 其中 m =2πfm 奈奎斯特周期: 2 7
7 §3.9 抽样定理sampling theorem • (一)时域抽样定理——奈奎斯特定理(Nyquist) 一个频率有限信号 如果频谱只占据 的范围,则信号 可以用等间隔的抽样值来唯一地表 示。而抽样间隔 不大于 ,或者说最低抽样频率 为 。 奈奎斯特频率: 或 其中 奈奎斯特周期: f (t) m m f (t) m 2 f 1 m m 2 f m 2 f s m f 2 f Ts m s f T 2 1 s 2 m
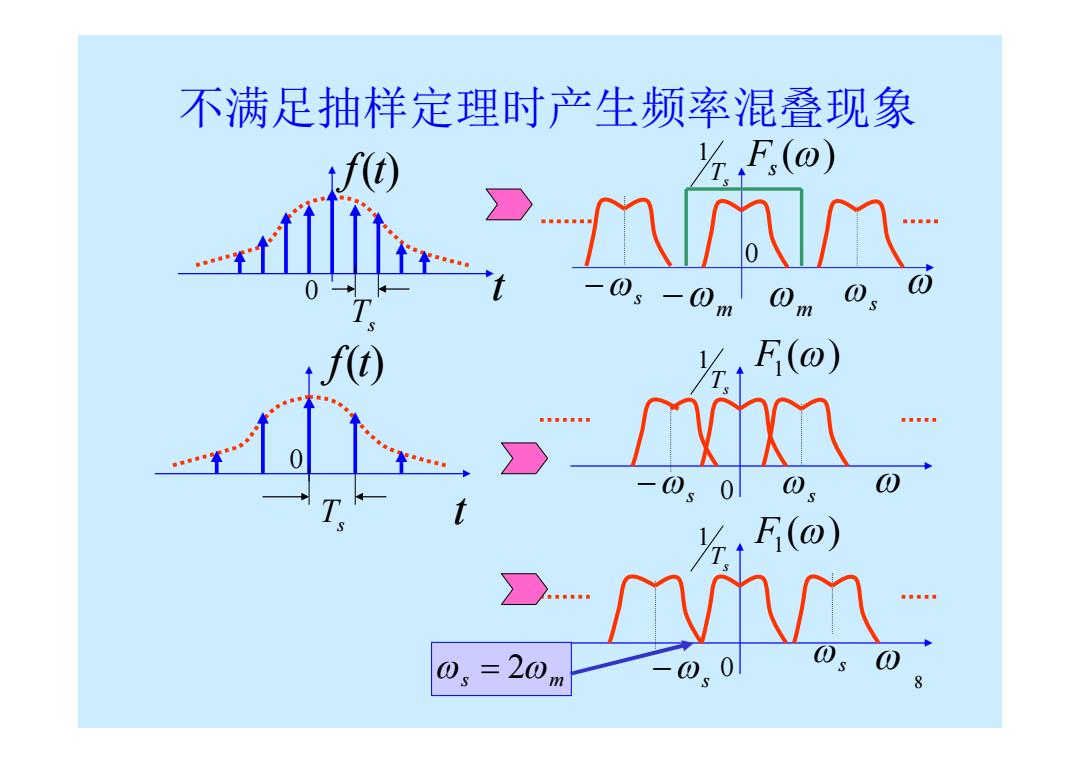
不满足抽样定理时产生频率混叠现象 六F,(⊙) F(@) O F(O) 0,=20 0 m
8 不满足抽样定理时产生频率混叠现象 0 t f(t) Ts ( ) F1 s 0 s Ts 1 () Fs 0 f(t) 0 t Ts 1 s Ts s m m ( ) F1 0 s s Ts 1 s 2 m