
3.2.1方差和中误差 设对某一未知量x进行次等精度观测,其观测值分别为 1、2、.、1n,其相应的真误差为△1、△2、..、4n, 则定义该组观测值的方差D为 D=lim △+△号+…+△2] [AA] n→0 n 1→0 式中,4=-L:L为未知量的真值。 显然,方差D是当观测次数→∞时,△的理论平均值
3.2.1 方差和中误差 设对某一未知量x进行n次等精度观测,其观测值分别为 l1、l2、......、ln,其相应的真误差为Δ1、Δ2、……、Δn, 则定义该组观测值的方差D为 22 2 1 2 lim lim n n n D n n 式中,Δi=li - L;L为未知量的真值。 显然,方差D是当观测次数n→∞时,i2 的理论平均值

3.2.1方差和中误差 标准偏差的定义为: o=√D=lim △+△3+..△ =lim △△] n->oo n n-→0 n 当为有限值时,按有限次数观测值的偶然误差求得的 标准偏差称为中误差。 测量学中常用m来表示中误差的估值。 m=±6=± △2+△3+..△ △△] n n
3.2.1 方差和中误差 当n为有限值时,按有限次数观测值的偶然误差求得的 标准偏差称为中误差。 测量学中常用m来表示中误差的估值。 22 2 ΔΔ Δ 1 2 [ΔΔ] ˆ n m n n 22 2 ΔΔ Δ 1 2 [ΔΔ] lim lim n n n D n n 标准偏差的定义为:
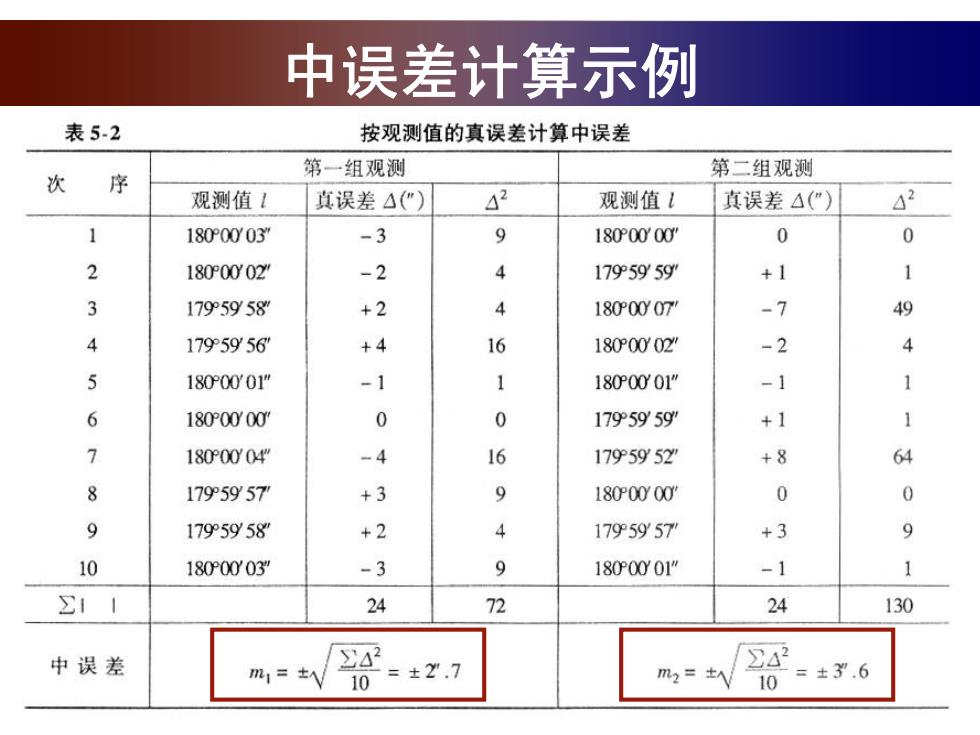
中误差计算示例 表5-2 按观测值的真误差计算中误差 第一组观测 第二组观测 次 序 观测值1 真误差△(") 42 观测值( 真误差△(") 2 1 1800003" -3 9 1800000W 0 0 2 180r0002z -2 4 179595gy +1 1 3 1795958 +2 4 180r0007 -7 49 1795956 +4 16 1800002" -2 4 1800001" -1 1 1800001" -1 1 6 180P0000 0 0 1795959 +1 7 1800004 -4 16 1795952 +8 6 1795957 +3 9 180T0000 0 0 9 1795958 +2 4 1795957 +3 9 10 1800003" -3 9 180P0001" -1 1 24 72 24 130 中误差 m1=人 10 =±Y.7 m2=±A 10 =±3Y.6
中误差计算示例

中误差计算示例 m1=±2.7"为第一组观测值的中误差; m2=±3.6”为第二组观测值的中误差。 m小于m2,说明第一组观测值的误差分布比较集中,其 精度较高;相反,第二组观测值的误差分布比较离散,其 精度较低。 精度的度量是对一组观测值 y=f(A) 而言,因而是个集合的概念。 (4】 同一精度的一组观测值,各观 测值的真误差可能不同,但各 3(4) 观测值的精度却是相同的
m1小于m2,说明第一组观测值的误差分布比较集中,其 精度较高;相反,第二组观测值的误差分布比较离散,其 精度较低。 m1 = 2.7 为第一组观测值的中误差; m2 = 3.6 为第二组观测值的中误差。 中误差计算示例 精度的度量是对一组观测值 而言,因而是个集合的概念。 同一精度的一组观测值,各观 测值的真误差可能不同,但各 观测值的精度却是相同的

3.2.2极限误差 由偶然误差的第一个特性可知,偶然误差的绝对值不会 超过一定的限值,该限值称为极限误差。 根据误差分布的概率密度函数,误差出现在微小区间d☑ 内的概率为: 2 P(A)=f(△)d△= dA √2πm 误差出现在K倍中误差区间内的既率为: Δ2
由偶然误差的第一个特性可知,偶然误差的绝对值不会 超过一定的限值,该限值称为极限误差 。 3.2.2 极限误差 2 2 2 1 ( ) 2 km m km P km e d m 2 2 2 1 () () 2 m P f d ed m 根据误差分布的概率密度函数,误差出现在微小区间 d 内的概率为: 误差出现在 K倍中误差区间内的概率为: