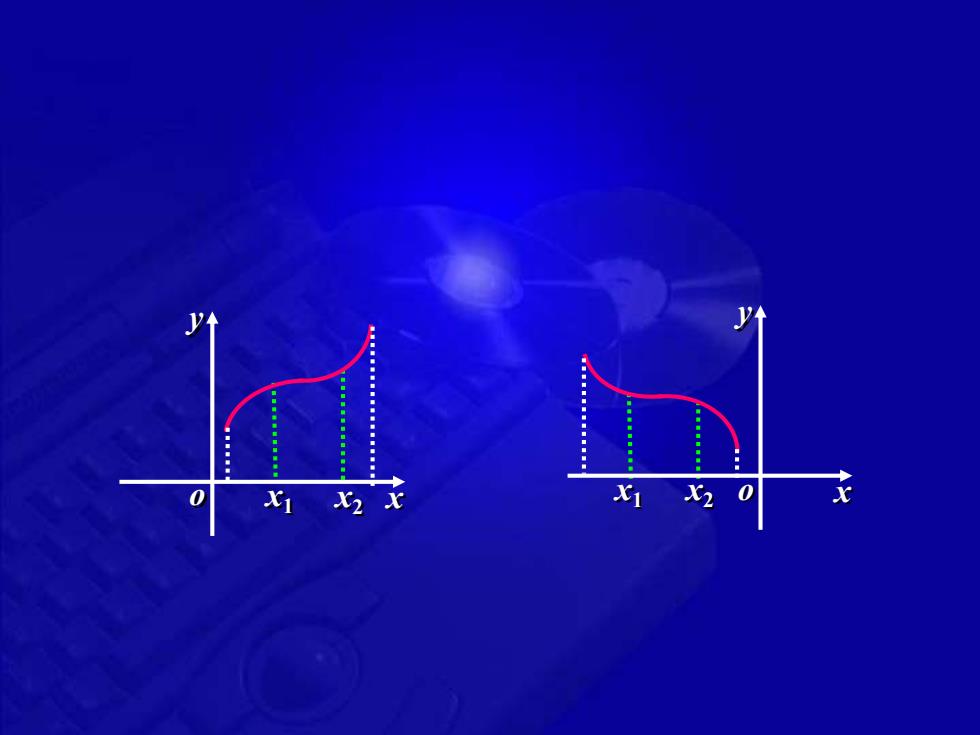
0 12x X2 0
x 1 x 2 o x x 1 x 2 y o x y

函数的单调性 () 概念 (二)判定 (三)应用
一、函数的单调性 (一)概念 (二)判定 (三)应用

一、函数的单调性 (一) 概念 (二) 判定 (三) 应用
一、函数的单调性 (一)概念 (二)判定 (三)应用
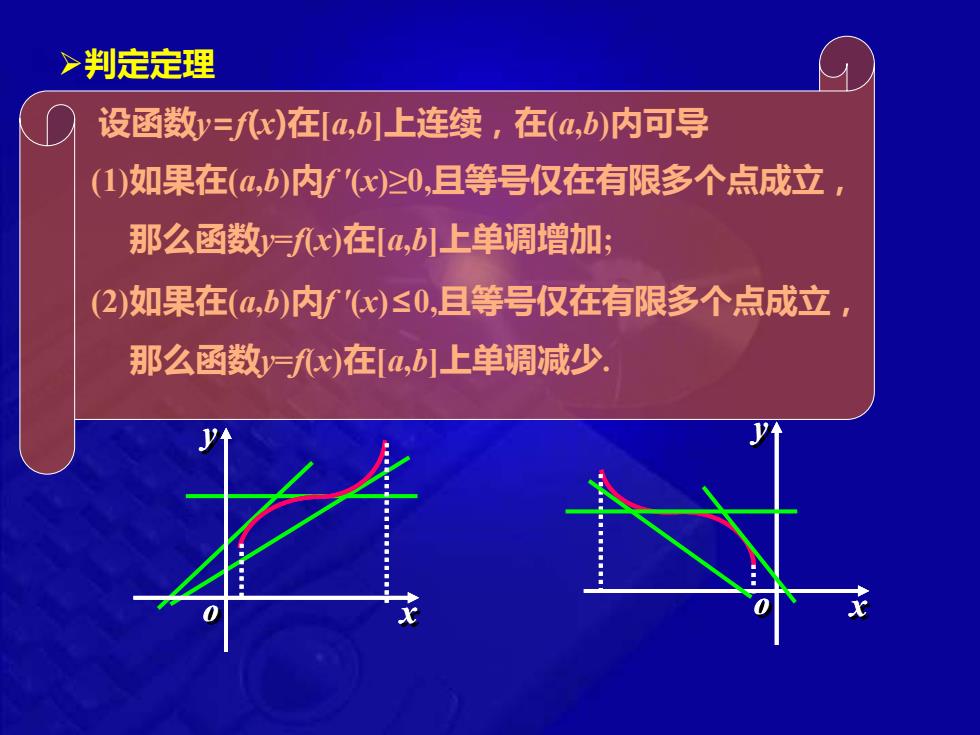
>判定定理 设函数y=f)在[a,上连续,在(a,b)内可导 (1)如果在(a,b)内f'x)≥0,且等号仅在有限多个点成立, 那么函数yfx)在a,b上单调增加; (2)如果在(a,b)内f'x)≤0,且等号仅在有限多个点成立, 那么函数y=fx)在a,b1上单调减少
o x y ➢判定定理 设函数y=f(x)在[a,b]上连续,在(a,b)内可导 (1)如果在(a,b)内f '(x)≥0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调增加; (2)如果在(a,b)内f '(x)≤0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调减少. o x y

>判定定理 设函数y三f八x)在a,b1上连续,在(a,b)内可导 (1)如果在(a,b)内f'x)≥0,且等号仅在有限多个点成立, 那么函数y=fx)在4,b上单调增加; (2)如果在(a,b)内f'(x)≤0,且等号仅在有限多个点成立 那么函数y=x)在[a,上单调减少, ◆例1判定函数y=x-sin在[0,2x]上的单调性 ◆例2讨论函数y=ex-x-1的单调性 ◆例3讨论函数y=)x的单调性
➢判定定理 设函数y=f(x)在[a,b]上连续,在(a,b)内可导 (1)如果在(a,b)内f '(x)≥0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调增加; (2)如果在(a,b)内f '(x)≤0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调减少. ◆例1 判定函数 y x x = − sin 在 0,2 上的单调性 ◆例2 讨论函数 1 x y e x = − − 的单调性 ◆例3 讨论函数 3 2 y x = 的单调性 o x y