即正、负电荷中心分别在y轴上距中心0为迟处 题7.山设匀强电场的电场强度E与半径为及的半球面的对称轴平行,试计算通过此半球 而的电场强度通量。 题710分析方法1:由电场强度通量的定文,对半球面5求积分,即中,-ES。 方法2:作半径为R的平面5S与半球面S一起可构成用合由面,由于用合面内无电荷。由高 斯定理 fE5=Σ9=0 这表明穿过闭合由面的净通量为零,宴入平面S“的电场强度通量在数值上等于穿出半 球面S的电场强度通量。因而 巾=fEd5=fnEd5 解1:取球坐标系。电场强度矢量和面元在球坐标系中可表示为 E=E(cosee +singea+sine, ds=R'sn阳0dpe, 中=fE-dS=∫,ER'sn0sm0up =后ERsn闲sme ■RE 解2:由于闭合由面内无电荷分布,根据高斯定理,有 p-fEds-于.Eds 依到约定取闭合由面的外法线方向为面元45的方向, 单=-E·成心0sr=RE 题71山:边长为a的立方体如图所示,其表面分别平行于、口和三平面,立方体的一个 顶点为坐标原点。现将立方体置于电场强度E=(后+城+E的非均匀电场中,求电场对立 方体各表面及整个文方体表面的电场盛度通量, 思71山解:参见因。由愿意E与O四面平行,所以对任何与Ow面平行的立方体表面。电 场强度的通量为零,即中x=e=0。而 中=jE4s=《5,+k+B,ds刀 -Ea 考虑到面CDEO与面AGF的外法线方向相反, 且该两面的电场分布相同,故有 pe=-中wn=-E,0 同理nm=∫E-d5=jIEi+E(-d5=-5a 的e-E:ds-JKE,+kaw+E(ds0-(E+ka加
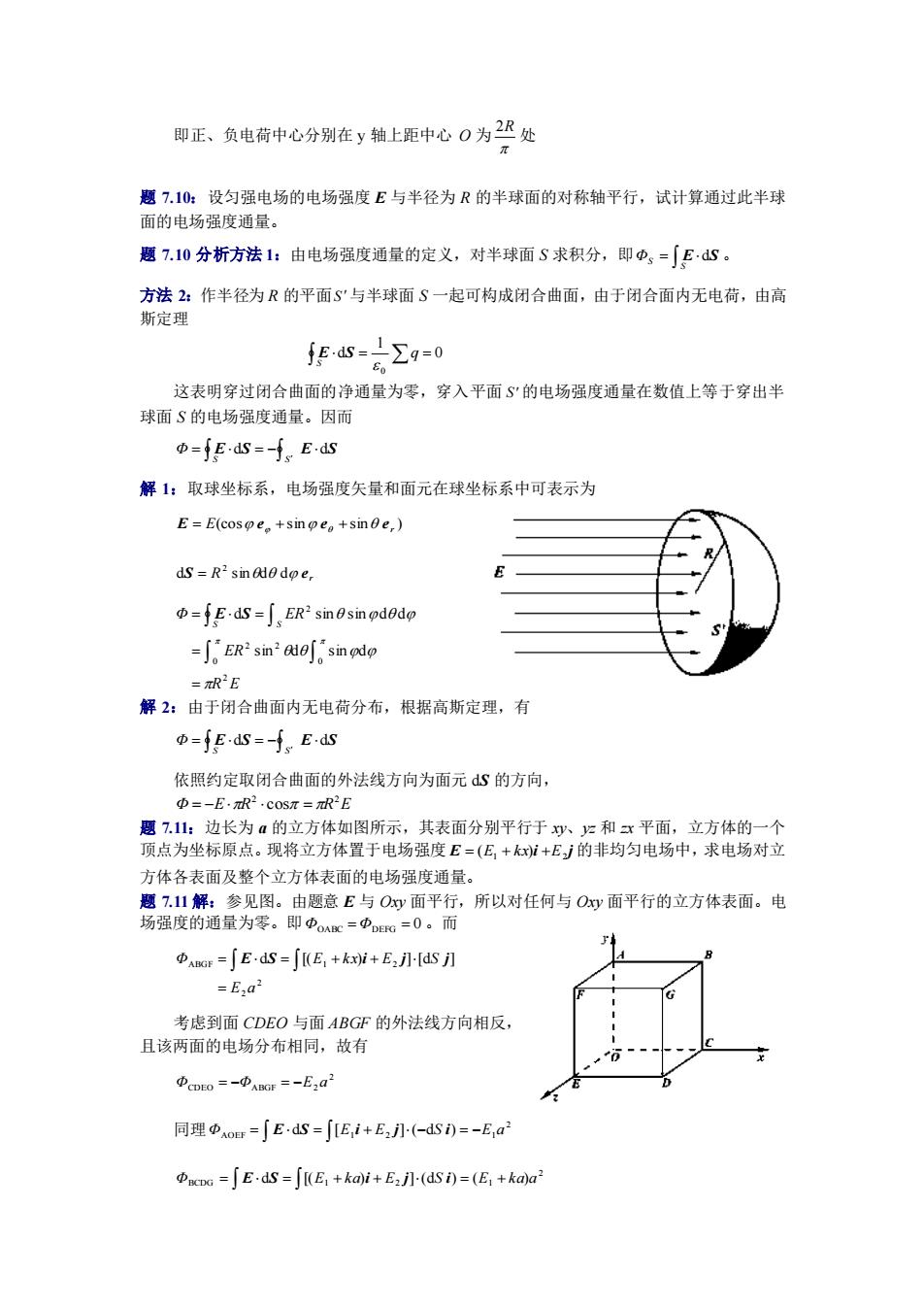
即正、负电荷中心分别在 y 轴上距中心 O 为 2R 处 题 7.10:设匀强电场的电场强度 E 与半径为 R 的半球面的对称轴平行,试计算通过此半球 面的电场强度通量。 题 7.10 分析方法 1:由电场强度通量的定义,对半球面 S 求积分,即 = S ΦS E dS 。 方法 2:作半径为 R 的平面 S 与半球面 S 一起可构成闭合曲面,由于闭合面内无电荷,由高 斯定理 0 1 d 0 = = q S E S 这表明穿过闭合曲面的净通量为零,穿入平面 S 的电场强度通量在数值上等于穿出半 球面 S 的电场强度通量。因而 = = − S S Φ E dS E dS 解 1:取球坐标系,电场强度矢量和面元在球坐标系中可表示为 (cos sin sin ) E r E e e e = + + R r dS sind d e 2 = R E ER Φ ER S S 2 0 0 2 2 2 sin d sin d d sin sin d d = = = = E S 解 2:由于闭合曲面内无电荷分布,根据高斯定理,有 = = − S S Φ E dS E dS 依照约定取闭合曲面的外法线方向为面元 dS 的方向, Φ E R R E 2 2 = − cos = 题 7.11:边长为 a 的立方体如图所示,其表面分别平行于 xy、yz 和 zx 平面,立方体的一个 顶点为坐标原点。现将立方体置于电场强度 E i j 1 2 = (E + kx) +E 的非均匀电场中,求电场对立 方体各表面及整个立方体表面的电场强度通量。 题 7.11 解:参见图。由题意 E 与 Oxy 面平行,所以对任何与 Oxy 面平行的立方体表面。电 场强度的通量为零。即 ΦOABC = ΦDEFG = 0 。而 2 2 ABGF 1 2 d [( ) ] [d ] E a Φ E k x E S = = = + + E S i j j 考虑到面 CDEO 与面 ABGF 的外法线方向相反, 且该两面的电场分布相同,故有 2 ΦCDEO = −ΦABGF = −E2 a 同理 2 AOEF 1 2 1 Φ = d = [E + E ](−dS ) = −E a E S i j i 2 BCDG 1 2 1 Φ = d = [(E + k a) + E ](dS ) = (E + k a)a E S i j i

因此。整个立方体表面的电场强度通量 中=∑=d 题712,地球周围的大气犹如一部大电机,由于雷雨云和大气气流的作用,在晴天区域,大 气电离层总是带有大量的正电载,云层下地球表面必然带有负电荷。睛天大气电场平均电场 强度约为0Vm',方向指向地面。试求地球表面单位面积所带的电背(以每平方厘米的 电子数表示)。 题711分析,考虑到地球表面的电场强度指向地球球心,在大气层中取与地球问心的球面 为高斯面,利用高斯定理可求得高斯面内的净电荷, 解:在大气层临近地球表面处取与地球表面同心的球面为高斯面,其半径R=R。(为地 球平均半径)。由高斯定理 ffd5=-6a成= 地球表面电荷面密度 a-∑9g/48-6,E=-106x10Cm 单位面积额外电子数 n=c-e)=6.63×l0'cm 题7,13:设在半径为R的球体内,其电荷为对称分布,电背体密度为 p=kr 05rs月 p=0 r>R 最为一常量。试用高斯定理求电场强度E与?的函数关系。(你能用电场强度叠加原理求解 这个月盟明?) 题7,13分析:通常有两种处理方法:(1)利用高斯定理求球内外的电场分布。由题意知电 背呈球对移分布,因面电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面 上电场强度大小为常量,且方向垂直于球面,因面有 fE-ds=E-4m' 根据高斯定律fE·5。二」Ψ,可解得电场强度的分布 6。 (2)利用带电球壳电场叠如的方法求球内外的电场分布。将带电球分制成无数个月心 带电球壳,球壳带电荷为山·P4容山',每个带电球壳在壳内激爱的电场dE=0,而在球 壳外激发的电场 dE=pdy 6, 由电场叠加可解得箭电球体内外的电场分布 E(r)-JE 0gF≤R Er)-['E r>R 解:因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定律
因此,整个立方体表面的电场强度通量 3 Φ =Φ = ka 题 7.12:地球周围的大气犹如一部大电机,由于雷雨云和大气气流的作用,在晴天区域,大 气电离层总是带有大量的正电荷,云层下地球表面必然带有负电荷。晴天大气电场平均电场 强度约为 120 Vm−,方向指向地面。试求地球表面单位面积所带的电荷(以每平方厘米的 电子数表示)。 题 7.11 分析:考虑到地球表面的电场强度指向地球球心,在大气层中取与地球同心的球面 为高斯面,利用高斯定理可求得高斯面内的净电荷。 解:在大气层临近地球表面处取与地球表面同心的球面为高斯面,其半径 R RE (RE 为地 球平均半径)。由高斯定理 = −E R = q S 0 2 E 1 d 4 E S 地球表面电荷面密度 9 2 0 2 4 E 1.06 10 C m − − =q R − E = − 单位面积额外电子数 5 2 ( ) 6.63 10 cm− n = −e = 题 7.13:设在半径为 R 的球体内,其电荷为对称分布,电荷体密度为 r R kr r R = = 0 0 k 为一常量。试用高斯定理求电场强度 E 与 r 的函数关系。(你能用电场强度叠加原理求解 这个问题吗?) 题 7.13 分析:通常有两种处理方法:(1)利用高斯定理求球内外的电场分布。由题意知电 荷呈球对称分布,因而电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面 上电场强度大小为常量,且方向垂直于球面,因而有 2 d E 4 r S = E S 根据高斯定律 = V S d 1 d 0 E S ,可解得电场强度的分布 (2)利用带电球壳电场叠加的方法求球内外的电场分布。将带电球分割成无数个同心 带电球壳,球壳带电荷为 dq = 4 r dr 2 ,每个带电球壳在壳内激发的电场 dE = 0,而在球 壳外激发的电场 r r V E e 2 4 0 d d = 由电场叠加可解得带电球体内外的电场分布 r r R r = ( ) d 0 0 E E r r R R = 0 E( ) dE 解 1:因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定律