《计量经济学》课程教学资源（PPT课件）课程PPT教学课件（第3版）第六章 联立方程计量经济模型理论方法 The Theory and Methodology of the Simultaneous-Equations Econometrics Model（SEM，2/2）

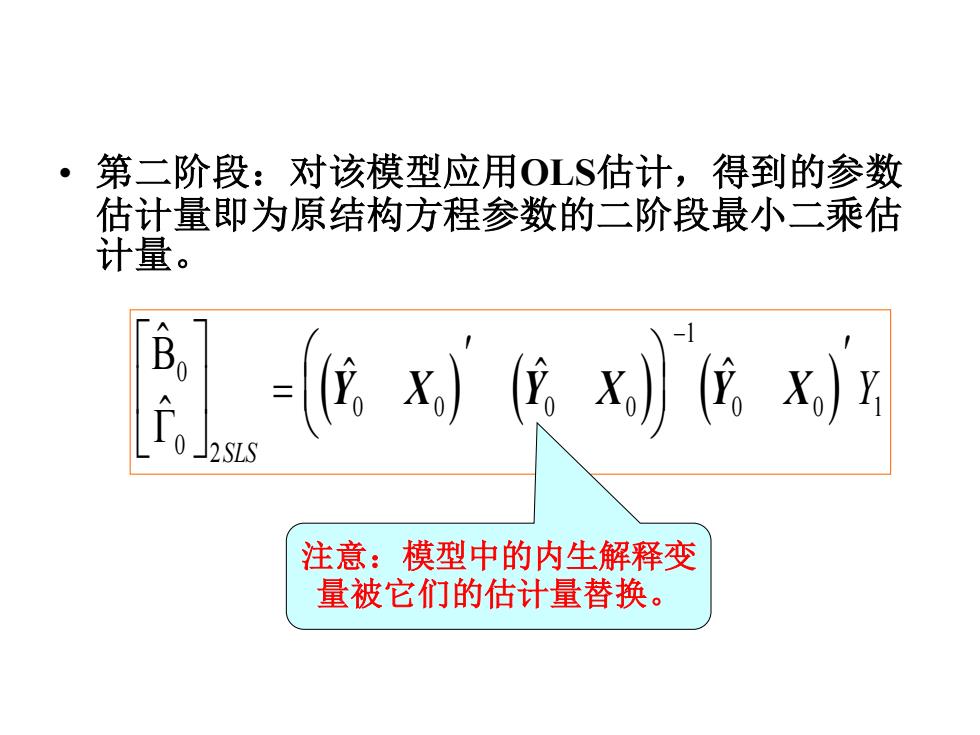
。子 第二阶段：对该模型应用OLS估计，得到的参数 估计量即为原结构方程参数的二阶段最小二乘估 计量。 Bo 广 区x信x信x 注意：模型中的内生解释变 量被它们的估计量替换

• 第二阶段：对该模型应用OLS估计，得到的参数 估计量即为原结构方程参数的二阶段最小二乘估 计量。 ( ) ( ) ( )        0 0 2 0 0 0 0 1 0 0 1       =         − SLS Y X Y X Y X Y 注意：模型中的内生解释变 量被它们的估计量替换

3.二阶段最小二乘法也是一种工具变量方法 。 如果用Y的估计量作为工具变量，按照工具变量方 法的估计过程，应该得到如下的结构参数估计量： Bo 馆x)化信x) ·可以严格证明两组参数估计量是完全等价的，所 以可以把2$LS也看成为一种工具变量方法。 ·证明过程见《计量经济学一方法与应用》（李子奈编著， 清华大学出版社，1992年3月)第130一131页

⒊二阶段最小二乘法也是一种工具变量方法 • 如果用Y0的估计量作为工具变量，按照工具变量方 法的估计过程，应该得到如下的结构参数估计量： ( ) ( ) ( )       0 0 0 0 0 0 1 0 0 1       =         − Y X Y X Y X Y • 可以严格证明两组参数估计量是完全等价的，所 以可以把2SLS也看成为一种工具变量方法。 • 证明过程见《计量经济学—方法与应用》（李子奈编著， 清华大学出版社，1992年3月）第130—131页

五、三种方法的等价性证明

五、三种方法的等价性证明

1.三种单方程估计方法得到的参数估计量 -((x x.)x.)(x;x.)'x A =,X =民x)化x)信x

⒈三种单方程估计方法得到的参数估计量 ( ) ( ) ( )    * *  0 0 0 0 0 0 1 0 0 1       =         − IV X X Y X X X Y ( ( ))     0 0 0 0 1 1       =   − ILS X Y X X Y ( ) ( ) ( )       0 0 2 0 0 0 0 1 0 0 1       =         − SLS Y X Y X Y X Y

2.IV与ILS估计量的等价性 。 在恰好识别情况下 ·工具变量集合相同，只是次序不同。 ·工具变量次序不同不影响正规方程组的解

⒉IV与ILS估计量的等价性 • 在恰好识别情况下 • 工具变量集合相同，只是次序不同。 • 工具变量次序不同不影响正规方程组的解