
第11章静电场 §11.1静电学基本问题 §11.2电场电场强度 §11.3高斯定理及应用 §11.4环路定理与电势 §11.5电势与电场强度的关系 静电场部分习题课内容
第 11 章 静电场 §11.1 静电学基本问题 静电学基本问题 §11.2 电场 电场强度 §11.3 高斯定理及应用 高斯定理及应用 §11.4 环路定理与电势 环路定理与电势 §11.5 电势与电场强度的关系 电势与电场强度的关系 静电场部分习题课内容 静电场部分习题课内容

§11.5电势与电场强度的关系 一、等势面 将电势相等的场点连成连续的曲画 一等势面。 满足方程: V(x,y,z)=c 通常约定相邻等势面的电势差 为常量,可以得到一系列的等 势面 △V2=△V23
一、等势面 V1 Δ 12 = ΔVV 23 ( ,, ) = czyxV 通常约定相邻等势面的电势差 为常量,可以得到一系列的等 势面 §11.5 电势与电场强度的关系 电势与电场强度的关系 将电势相等的场点连成连续的曲面— —等势面。 满足方程: V2 V3

二、等势面的性质 1.电荷沿等势面移动,电场力不做功。 Aab=-qUbo=-q0=0 2.电场强度与等势面正交;电力线由电势高的地方指向 电势低的地方。 (ad4=gE.d7=0→Edi=0 b)A2=-(W-W)=-9U2-U),当q>0时,A2>0 →U2-U1<0 →U>U2 3.相邻等势面间距小处,场强大;间距大处, 场强小。E·△l=Const.→Eoc1/△l
二、等势面的性质 1. 电荷沿等势面移动,电场力不做功。 ab −= qUA ba= −q ⋅0 2. 电场强度与等势面正交;电力线由电势高的地方指向 电势低的地方。 lEqA r r ⋅= dd ≡ 0 lE ≡⋅ 0d r r (a) (b) )( 12 −= −WWA 12 0 0 当 > 时,QAq 12 > ⇒ −UU 12 < 0 >⇒ UU 21 3. 相邻等势面间距小处,场强大;间距大处, 场强小。 ⋅ΔlE = .Const ⇒ ∝1 ΔlE ),( = − −UUq 12 = 0
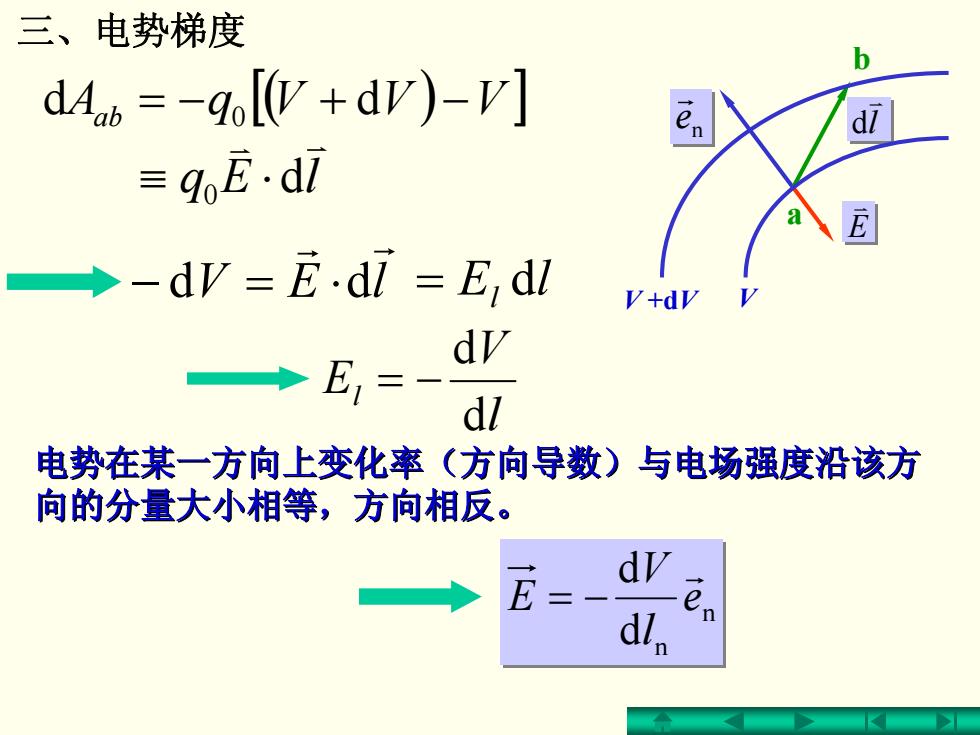
三、电势梯度 b dA=-qo[W+d)-V] dl =go.d7 →-dV=E.di=E,dl V+dV dV E,= dl 电势在某一方向上变化率(方向导数)与电场强度沿该方 向的分量大小相等,方向相反
三、电势梯度 n e r E v b a l v d d ab = − 0 [ ] ( + d )−VVVqA lEV r r ⋅=− dd l V El dd −= 电势在某一方向上变化率(方向导数)与电场强度沿该方 电势在某一方向上变化率(方向导数)与电场强度沿该方 向的分量大小相等,方向相反。 向的分量大小相等,方向相反。 lEq v v d 0 ⋅≡ = l dlE n n d d e l V E r −= V +dV V
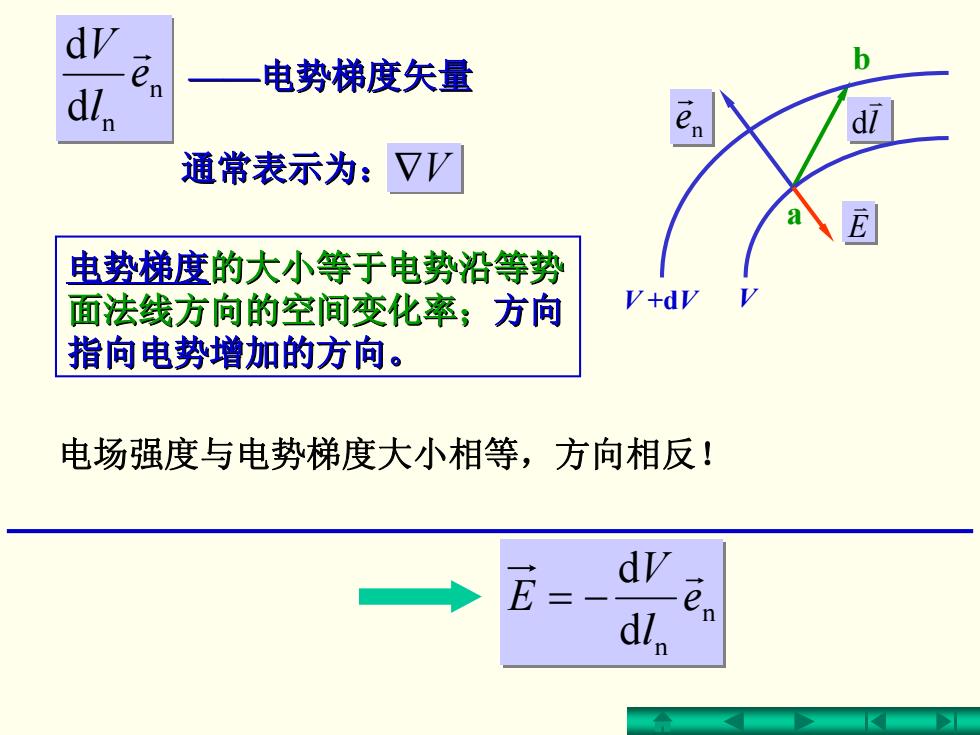
d/. n 电势梯度矢量 dl 通常表示为:VV 电势梯度的大小等于电势沿等势 面法线方向的空间变化率;方向 V+dV 指向电势增加的方向。 电场强度与电势梯度大小相等,方向相反! E d dl
n n d d e l V E r −= n e r b a l v d V +dV V E v ——电势梯度矢量 通常表示为:∇V 电势梯度的大小等于电势沿等势 的大小等于电势沿等势 面法线方向的空间变化率; 面法线方向的空间变化率;方向 指向电势增加的方向。 指向电势增加的方向。 电场强度与电势梯度大小相等,方向相反! n n d d e l V r