
第10章气体和疑聚态
第 10 章 气体和凝聚态

气体和疑聚态 §10.1范德瓦耳斯方程 §10.2气体内的输运过程 §10.3固体和液体的热性质
§10.1 范德瓦耳斯方程 第 10 章 气体和凝聚态 §10.2 气体内的输运过程 §10.3 固体和液体的热性质
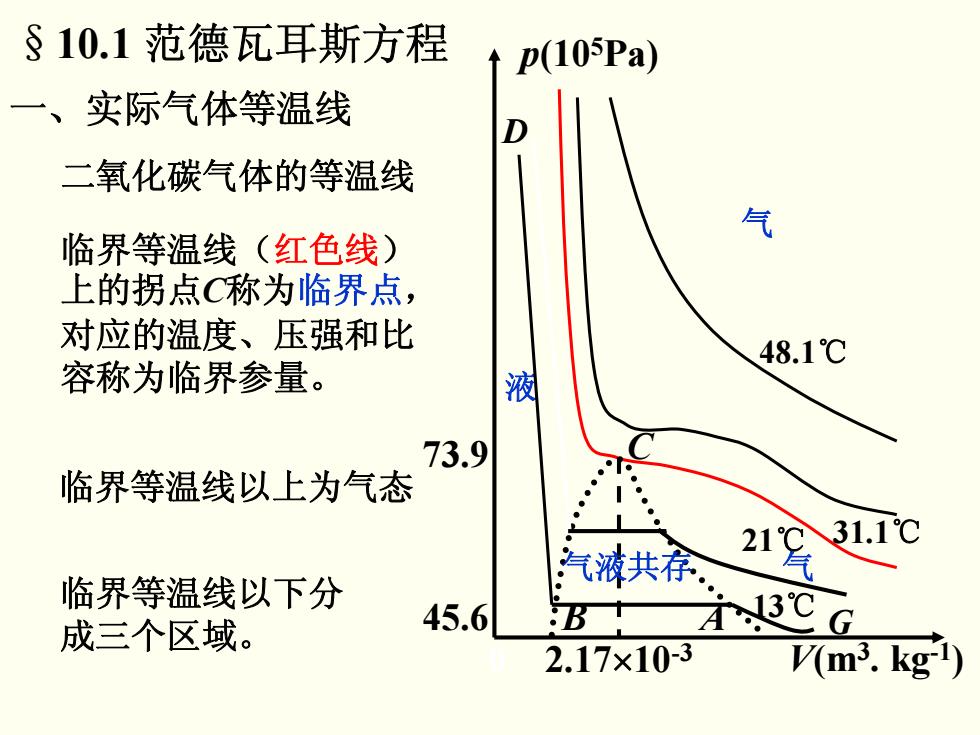
§10.1范德瓦耳斯方程 p(105Pa) 一、实际气体等温线 二氧化碳气体的等温线 气 临界等温线(红色线) 上的拐点C称为临界点, 对应的温度、压强和比 48.1℃ 容称为临界参量。 液 73.9 临界等温线以上为气态 临界等温线以下分 气液共。 2 成三个区域。 45.6 B 3℃ G 2.17×10-3 V(m3.kg-1)
二氧化碳气体的等温线 临界等温线以上为气态 临界等温线以下分 成三个区域。 一、实际气体等温线 48.1 ℃ 31.1 ℃ 13 ℃ 气 21 ℃ C 气液共存 气 液 §10.1 范德瓦耳斯方程 临界等温线(红色线 ) 上的拐点 C称为临界点 , 对应的温度、压强和比 容称为临界参量。 B A G D p(10 5Pa) V(m 3. kg-1 2.17 ×10 ) -3 73.9 45.6 0
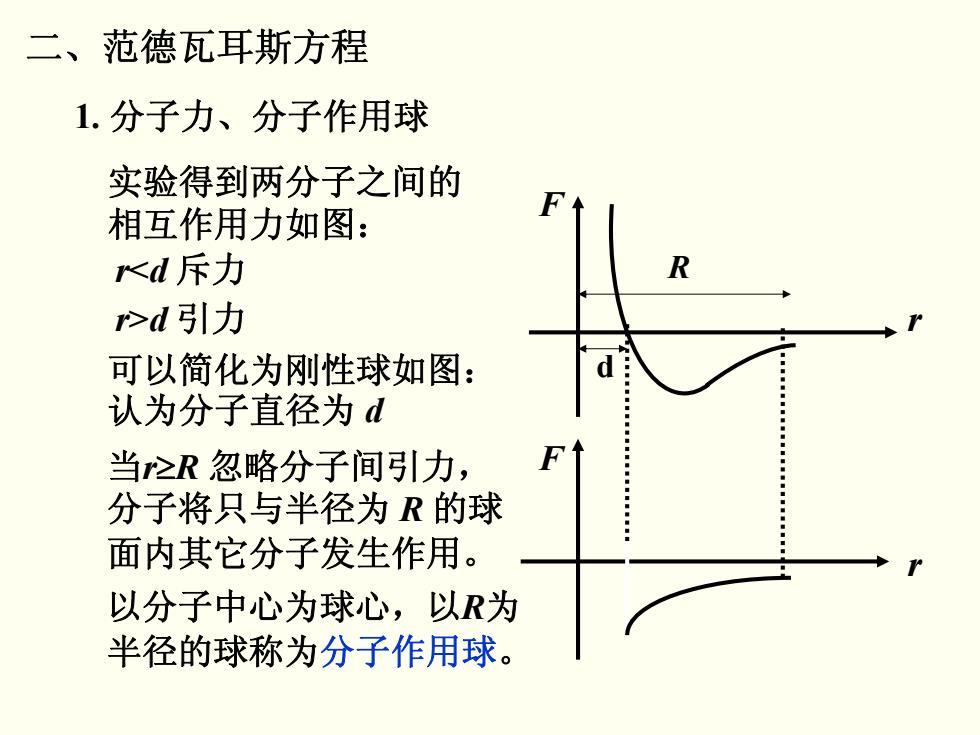
二、范德瓦耳斯方程 1.分子力、分子作用球 实验得到两分子之间的 相互作用力如图: <d斥力 >d引力 可以简化为刚性球如图: d 认为分子直径为d 当≥R忽略分子间引力, 分子将只与半径为R的球 面内其它分子发生作用。 以分子中心为球心,以R为 半径的球称为分子作用球
二、范德瓦耳斯方程 1. 分子力、分子作用球 F r F r d R 实验得到两分子之间的 相互作用力如图: r < d 斥力 r >d 引力 可以简化为刚性球如图: 认为分子直径为 d 当 r ≥R 忽略分子间引力, 分子将只与半径为 R 的球 面内其它分子发生作用。 以分子中心为球心,以 R 为 半径的球称为分子作用球

2.分子斥力的修正 1mol理想气体 PVn=RT Vm容器容积,气体可压缩体积 现分子为刚性球,气体分子本身占有体积, 气体可压缩体积应有修正。 p(Vm-b)=RT d 理论上b约为分子本身体积的4倍b=4NA3元) 标准状态 1 mol=22.4×103m3 通常b可忽略,但压强增大,容积与b可比拟时, b的修正就必须了。 实际b值要随压强变化而变化
现分子为刚性球,气体分子本身占有体积 , 气体可压缩体积应有修正。 1mol理想气体 理论上 b 约为分子本身体积的 4 倍 通常 b 可忽略,但压强增大,容积与 b 可比拟时, b 的修正就必须了。 实际 b 值要随压强变化而变化。 2. 分子斥力的修正 m = RTpV m − )( = RTbVp 3 2 π 3 4 4 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = d Nb A 33 m m104.22 mol1 − 标准状态 V ×= Vm容器容积,气体可压缩体积