
第13章电介质 §13.1静电场中的电介质 §13.2介质中的高斯定理 §13.3介质边界两侧的静电场 §13.4静电场的能量
第 13 章 电介质 §13.2 介质中的高斯定理 介质中的高斯定理 §13.1 静电场中的电介质 静电场中的电介质 §13.4 静电场的能量 §13.3 介质边界两侧的静电场 介质边界两侧的静电场
§13.4静电场的能量 一、带电体系的静电能 若点电荷q0处于q的电场中, 静电能为: W.=4'=464元er 9 dr ◆把qo从P点移到无限远时 静电场力作的功,就是 ·d “系统”的静电势能。 或:把qo从无限远移动到P点的过 V=E.dF 程中,外力反抗静电力作的功
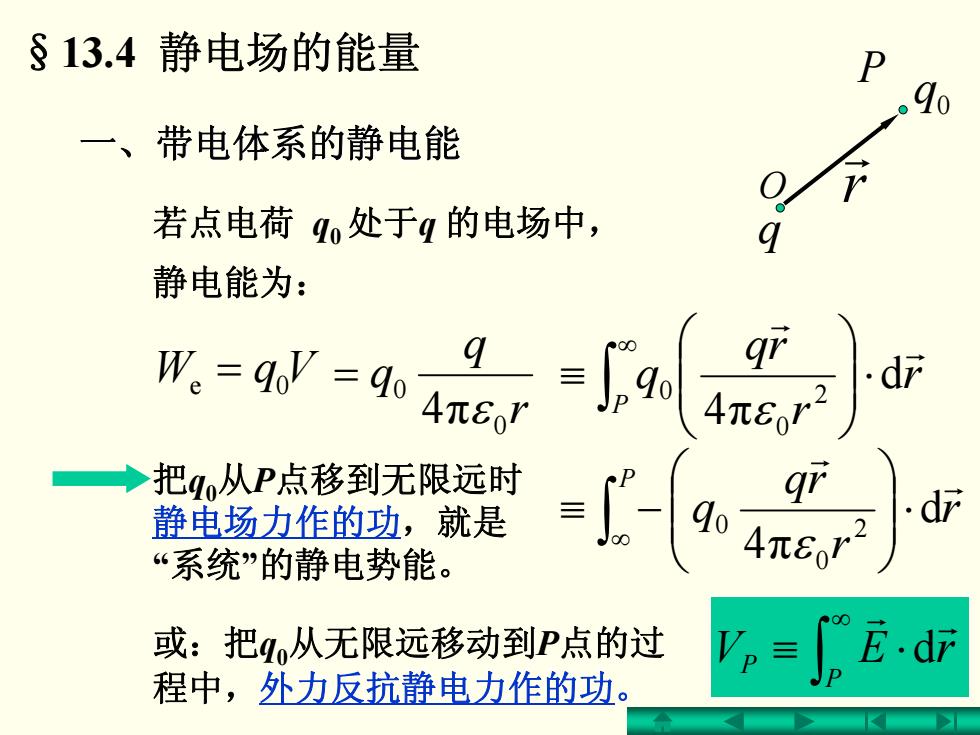
一、带电体系的静电能 带电体系的静电能 若点电荷 q0 处于q 的电场中, = 0e VqW 静电能为: §13.4 静电场的能量 r q q 0 0 4πε = ∫∞ ⋅ ⎟⎟⎠⎞ ⎜⎜⎝⎛ ≡ P r rrq q r r d 4π 2 0 0 ε r r q 0 q P O 把q0从P点移到无限远时 静电场力作的功,就是 “系统”的静电势能。 r r rq q P r r ∫∞ ⋅ ⎟⎟⎠⎞ ⎜⎜⎝⎛ −≡ d 4π 2 0 0 ε 或:把q0从无限远移动到P点的过 程中,外力反抗静电力作的功。 ∫∞ ⋅≡ P P rEV r r d

*对于点电荷体系(或连续带电体),系统的能 量可以有类似的定义: >把点电荷体系无限分离到彼此间相距无限远的 过程中静电场力作的功,叫作该系统内的静电势 能。 >对连续带电体,可以把带电体看成是由无限多 电荷元组成的点电荷体系。这样,连续带电体的 静电能量的定义同上
¾ 把点电荷体系无限分离到彼此间相距无限远的 过程中静电场力作的功,叫作该系统内的静电势 能。 ¾ 对连续带电体,可以把带电体看成是由无限多 电荷元组成的点电荷体系。这样,连续带电体的 静电能量的定义同上。 * 对于点电荷体系(或连续带电体),系统的能 量可以有类似的定义: 量可以有类似的定义:

二、点电荷系的能量 电势能: 91 W。=q24元6r 02 二q小4元60' =qK+9] 个点电荷系统的电势能:队。=)∑9,叫 其中,V,为除4:外其它点电荷在4:处产生的电势之和
二、点电荷系的能量 二、点电荷系的能量 q 2 r q qW 0 1 2e 4 π ε = 电势能: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ +⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = r q q r q qW 0 1 2 0 2 e 1 42 π 4 π 1 ε ε n个点电荷系统的电势能: 个点电荷系统的电势能: ∑= = n i VqW ii 1 e 2 1 q1 r q 2 [ ] 2211 2 1 += VqVq r q q 0 2 1 4 π ε = q 1 其中, Vi 为除 q i 外其它点电荷在 q i处产生的电势之和。 处产生的电势之和

三、连续带电体的静电能量 体状带电体:所.=广P八(pd) 面状带电体,化.=P(GdS) 线状带电体:.=V(2d > 式中V表示电荷元处的电势,原则上不包括该电荷元的贡 献。但由于电荷元的贡献为一阶小量,其中的差别可以忽略
三、连续带电体的静电能量 三、连续带电体的静电能量 = ∫ d q τ τρ )d( 2 1 体状带电体: e VW 面状带电体: ∫ = S SVW )d( 2 1 e σ 线状带电体: ∫ = L lVW )d( 2 1 e λ ¾ 式中 V 表示电荷元处的电势,原则上不包括该电荷元的贡 表示电荷元处的电势,原则上不包括该电荷元的贡 献。但由于电荷元的贡献为一阶小量,其中的差别可以忽略。 献。但由于电荷元的贡献为一阶小量,其中的差别可以忽略