
电路非正弦周期电流电路和信号的频谱注意利用函数的对称性可使系数的确定简化f (t)①偶函数b, =0f(t)= f(-t)T/2T②奇函数f(t)f(t)=-f(t)a, =0-T20T2t③奇谐波函数(t)T=0f(t)=-f(t+dak2k2KT22返上回页页N
利用函数的对称性可使系数的确定简化 ①偶函数 ( ) = (− ) = 0 k f t f t b ( ) = − ( ) = 0 k f t f t a ②奇函数 ③奇谐波函数 ) 0 2 ( ) ( = − + a2k = b2k = T f t f t 注意 -T/2 T/2 t f (t) o -T/2 T/2t f (t) o t f (t) o T/2 T 返 回 上 页 下 页
电路非正弦周期电流电路和信号的频谱山周期函数的频谱图:幅度频谱的图形Alm ~ ko,kmnko130 50, 700相位频谱的图形d~ka返上回页F页
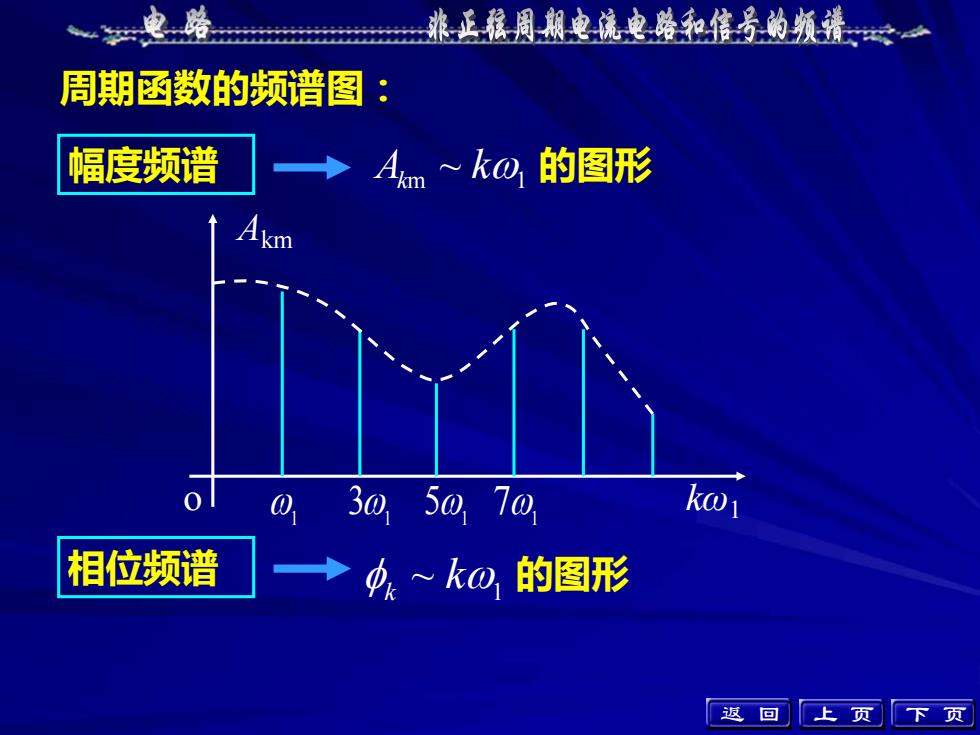
周期函数的频谱图: 幅度频谱 A k km 1 ~ 的图形 1 1 1 1 3 5 7 Akm o kω1 相位频谱 k ~ k 1 的图形 返 回 上 页 下 页

电路非正弦周期电流电路和信号的频谱山例1周期性方波信号的分解Tm2is(t)=TmC<t<T2T/2福T解图示矩形波电流在一个周期内的表达式为:/2直流分量:mdtis(t)dtLI。=7m2T谐波分量:bk=is(ot)sin kotd(@ t)4元K为偶数2]coskot)" =3k元K为奇数k元返上回页个页
例1 周期性方波信号的分解 解 图示矩形波电流在一个周期内的表达式为: = t T T T I t i t S 2 0 2 0 ( ) m 2 d 1 ( )d 1 0 / 2 0 m T T O S m I I t T i t t T 直流分量: I = = = 谐波分量: = 2π 0 ( )sin d( ) π 1 b i t k t t K S K为偶数 K为奇数 = − = π 2 0 cos ) 1 ( π π 0 k k t I k I m m t T/2 T S i m I o 返 回 上 页 下 页

非正弦周期电流电路和信号的频谱山22元i,(ot)coskotd(t)3O元21msin kotl"= 0k元21mA=b+α=bk(k为奇数)k元的展开式为:21mm-sin3t +=sin5ot +...sinot +元返上回页页K
sin 0 1 π 2 ( )cos d( ) π 2 π 0 2π 0 = = = k t k I a i t k t t m k S π 2 2 k 2 k k k I A b a b m = + = K = (k为奇数) s i 的展开式为: sin 5 ) 5 1 sin 3 3 1 (sin π 2 2 = + t + t + t + I I i m m S 返 回 上 页 下 页
#电路非正弦周期电流电路和信号的频谱周期性方波波形分解直流分量基波三次谐波七次谐波五次谐波返上回页F
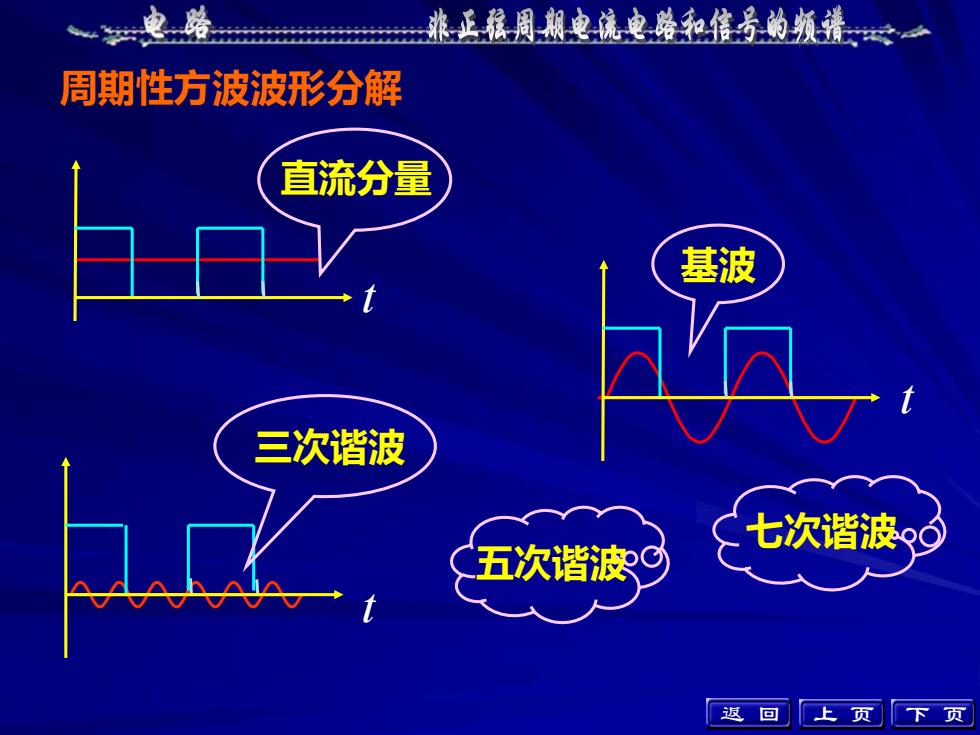
t t t 基波 直流分量 三次谐波 五次谐波 七次谐波 周期性方波波形分解 返 回 上 页 下 页